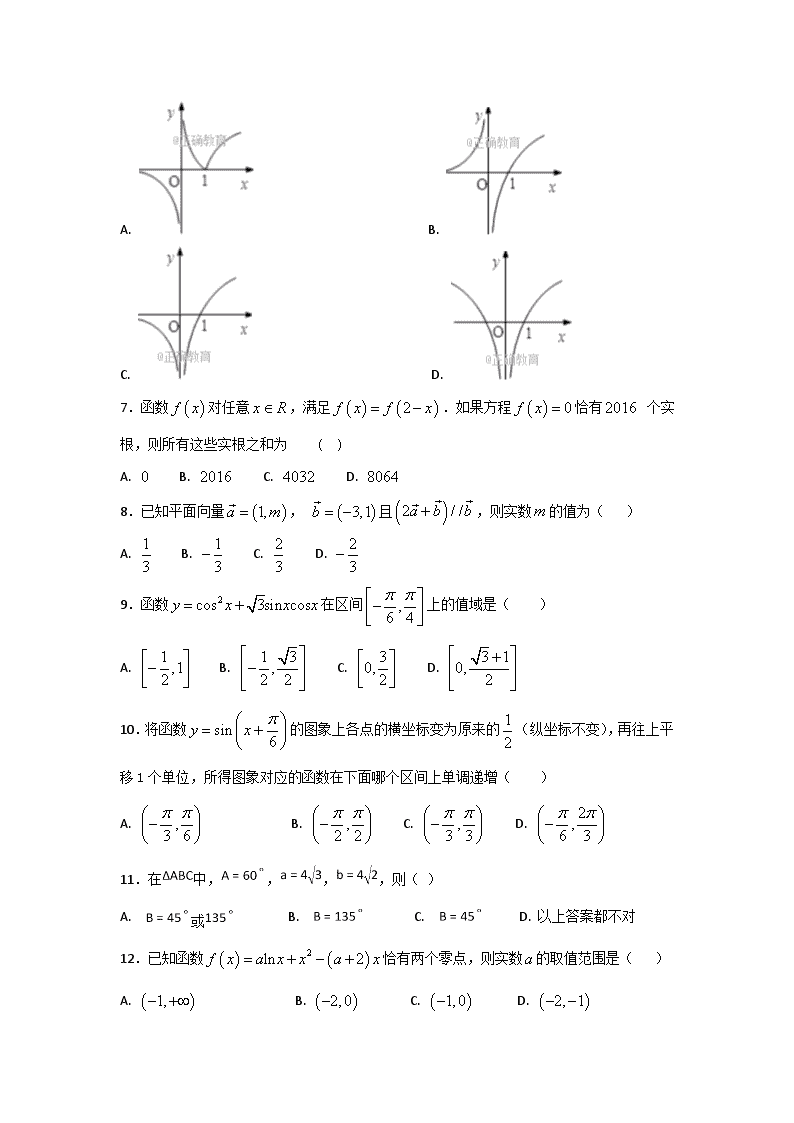- 906.50 KB
- 2021-04-17 发布
景县中学2018届高三10月月考
数学理试卷
第I卷(选择题)
一、选择题(每小题5分,共60分)
1.已知集合,则( )
A. B. C. D.
2.若复数在复平面内对应的点在第二象限,则实数的取值范围是
A. B. C. D.
3.下列说法中,正确的是( )
A. 命题“若,则”的否命题为“若,则”
B. 命题“存在,使得”的否定是:“任意,都有”
C. 若命题“非”与命题“或”都是真命题,那么命题一定是真命题
D. " "是" "的充分不必要条件
4.由曲线与直线, 所围成封闭图形的面积为( )
A. B. C. D.
5.已知函数是定义在上的偶函数,且在区间上单调递增.若实数满足,则a的取值范围是( )
A. B. C. D.
6.函数的图象大致是( )
A. B.
C. D.
7.函数对任意,满足.如果方程恰有 个实根,则所有这些实根之和为 ( )
A. B. C. D.
8.已知平面向量, 且,则实数的值为( )
A. B. C. D.
9.函数在区间上的值域是( )
A. B. C. D.
10.将函数的图象上各点的横坐标变为原来的(纵坐标不变),再往上平移1个单位,所得图象对应的函数在下面哪个区间上单调递增( )
A. B. C. D.
11.在中,,,,则( )
A. 或 B. C. D. 以上答案都不对
12.已知函数恰有两个零点,则实数的取值范围是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(每小题5分,共20分)
13.直线是曲线的一条切线,则实数__________.
14.已知向量满足,记向量的夹角为,则__________.
15.若,则_____________.
16.设函数在R上存在导数,对任意的 有 ,且在 上 .若 ,则实数的取值范围__________.
三、解答题(共70分)
17(10分).设命题:实数满足,其中;命题:实数满足.
(1)若,且为真,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
18(12分).已知函数.
(1)求 的值;
(2)求 的最小正周期及单调递增区间.
19(12分).如图为函数 图像的一部分.
(1)求函数 的解析式;
(2)若将函数 图像向在左平移 的单位后,得到函数 的图像,若,求x的取值范围.
20(12分).已知锐角中,内角的对边分别为,且.
(1)求角的大小;
(2)求函数的值域.
21(12分).已知函数.
(Ⅰ)当时,求的最大值与最小值;
(Ⅱ)讨论方程的实根的个数.
22(12分).已知函数.
(1)若是的极值点,求的极大值;
(2)求实数的范围,使得恒成立.
数学理试卷参考答案
1.C 2.B 3.C 4.A 5.C 6.C 7.B 8.B 9.C 10.A 11.C 12.C
13. 14. 15. 16.
17.(1) (2)
解:(1)由得,
又,所以,
当时, ,即为真时实数的取值范围是.
为真时等价于,得,
即为真时实数的取值范围是.
若为真,则真且真,所以实数的取值范围是.
(2)是的充分不必要条件,即,且,等价于,且,
设, ,则;
则,且所以实数的取值范围是.
18.(1) ;(2),().
(1) .
(2)
.
所以,的最小正周期为,
当()时,单调递增,
即的单调递增区间为().
19.(1);(2).
(1)由图像可知 ,函数图像过点,则,故
(2) ,即,即
20.(1);(2).
(1)由,利用正弦定理可得,
可化为: ,
.
(2)
21.(1) 最小值是,最大值是;(2) 时,方程有1个实根; 时,方程有3个实根.
(Ⅰ)因为,
所以,
令得, 的变化如下表:
在上的最小值是,
因为,
所以在上的最大值是.
(Ⅱ),
所以或,
设,则, 时, , 时, ,
所以在上是增函数,在上是减函数, ,
且,
(ⅰ)当时,即时, 没有实根,方程有1个实根;
(ⅱ)当时,即时, 有1个实根为零,方程有1个实根;
(ⅲ)当时,即时, 有2不等于零的实根,方程有3个实根.
综上可得, 时,方程有1个实根; 时,方程有3个实根.
22.(1)(2)
(1)
是的极值点
解得
当时,
当变化时,
递增
极大值
递减
极小值
递增
的极大值为.
(2)要使得恒成立,即时, 恒成立,
设,
则
(i)当时,由得函数单调减区间为,由得函数单调增区间为,此时,得.
(ii)当时,由得函数单调减区间为,由得函数单调增区间为,此时, 不合题意.
(iii)当时, 在上单调递增,此时, 不合题意
(iv)当时,由得函数单调减区间为,由得函数单调增区间为,此时, 不合题意.
综上所述: 时, 恒成立.