【数学】2018届一轮复习苏教版第67课时线面垂直、面面垂直的判定与性质（2）学案 5页

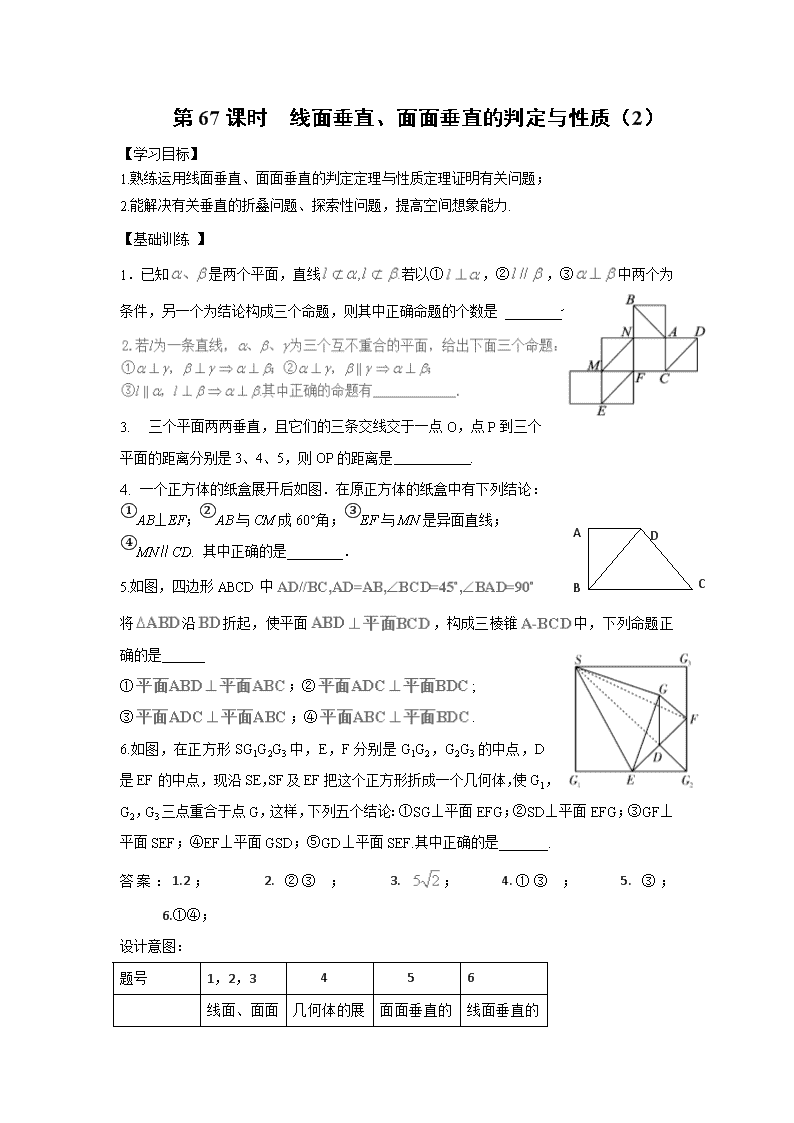
第67课时 线面垂直、面面垂直的判定与性质（2）‎ ‎【学习目标】‎ ‎1.熟练运用线面垂直、面面垂直的判定定理与性质定理证明有关问题；‎ ‎2.能解决有关垂直的折叠问题、探索性问题，提高空间想象能力.‎ ‎【基础训练 】‎ ‎1．已知是两个平面，直线若以①，②，③中两个为条件，另一个为结论构成三个命题，则其中正确命题的个数是 个。‎ ‎3. 三个平面两两垂直，且它们的三条交线交于一点O，点P到三个 平面的距离分别是3、4、5，则OP的距离是 .‎ ‎4. 一个正方体的纸盒展开后如图．在原正方体的纸盒中有下列结论：‎ D C B A ‎①AB⊥EF；②AB与CM成60°角；③EF与MN是异面直线；‎ ‎④MN∥CD. 其中正确的是________．‎ ‎5.如图，四边形ABCD中 将沿折起，使平面，构成三棱锥中，下列命题正确的是 ‎ ‎①；②; ‎ ‎③；④.‎ ‎6.如图，在正方形SG‎1G2G3中，E，F分别是G‎1G2，G‎2G3的中点，D是EF的中点，现沿SE，SF及EF把这个正方形折成一个几何体，使G1，G2，G3三点重合于点G，这样，下列五个结论：①SG⊥平面EFG；②SD⊥平面EFG；③GF⊥平面SEF；④EF⊥平面GSD；⑤GD⊥平面SEF.其中正确的是_______.‎ 答案：1.2； 2. ②③ ； 3. ； 4.①③ ； 5. ③； 6.①④； ‎ 设计意图：‎ 题号 ‎1，2，3‎ ‎4‎ ‎5‎ ‎6‎ 复习内容 线面、面面垂直，平行的综合应用 几何体的展开图问题 面面垂直的判定 ‎ 线面垂直的判定 教学建议：通过知识点的训练让学生熟练掌握线面垂直、面面垂直的性质和判定。.‎ ‎[来源: ]‎ ‎【典型例题】‎ 设计意图：(1)复习线面、面面垂直（平行）的判定和性质;‎ ‎ (2)要学会从不同的角度去观察几何体。‎ 教学建议：可以采用分析法寻找思路，用综合法书写过程。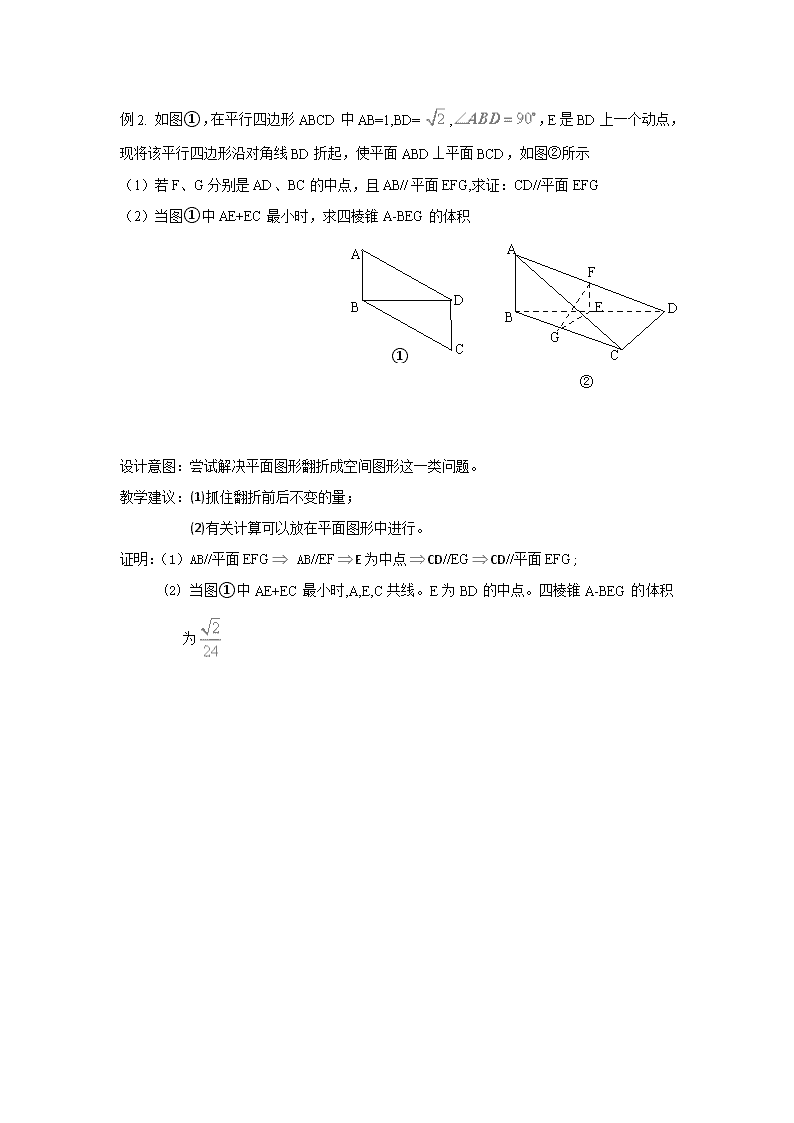‎ 证明：（1）证明A‎1CAC1, A‎1CB‎1C1.;(2)存在D是棱AB的中点.‎ 例2. 如图①，在平行四边形ABCD中AB=1,BD=,，E是BD上一个动点，现将该平行四边形沿对角线BD折起，使平面ABD⊥平面BCD，如图②所示 ‎（1）若F、G分别是AD、BC的中点，且AB//平面EFG,求证：CD//平面EFG ‎（2）当图①中AE+EC最小时，求四棱锥A-BEG的体积 G F E D C B A D C B A ‎①‎ ‎②‎ 设计意图：尝试解决平面图形翻折成空间图形这一类问题。‎ 教学建议：(1)抓住翻折前后不变的量；‎ ‎(2)有关计算可以放在平面图形中进行。‎ 证明：（1）AB//平面EFG AB//EFE为中点CD//EGCD//平面EFG;‎ ‎(2) 当图①中AE+EC最小时,A,E,C共线。E为BD的中点。四棱锥A-BEG的体积为 例3.如图所示,在直四棱柱中,, ,点是棱上一点.(1)求证：；(2)试确定点的位置,使得平面平面. ‎ M A B C D A1‎ B1‎ C1‎ D1‎ ‎ ‎ 设计意图：复习巩固证明线线、面面垂直的常用方法。‎ 教学建议：总结立体几何中证明垂直的常用方法：线线垂直←线面垂直→面面垂直。‎ 证明：（1）证明AC平面BDD1B1;(2)M为BB1的中点。‎ A B C D F E 例4.已知△BCD中,∠BCD=90,BC=CD=1,AB⊥平面BCD，∠ADB=60,E,F分别为AC,AD上的动点,且.‎ ‎(1)求证:无论λ为何值,总有平面BEF⊥平面ABC;[来源: ]‎ ‎(2)当λ为何值时,平面BEF⊥平面ACD ‎(3)求三棱锥A-BCD的体积 设计意图：面面垂直的问题中有关参数的取值问题。‎ 教学建议：注意使用分析法逆向思考问题。‎ 证明：（1）无论λ为何值,总有CD平面ABC,EF//CD，所以平面BEF⊥平面ACD;‎ ‎(2) ；‎ ‎(3) 。‎