- 1.57 MB
- 2021-04-17 发布
2018-2019学年河北省临漳县第一中学高二第三次月考数学试卷(理)
一、选择题(本大题共12小题,共60.0分)
1. ,则的一个必要不充分条件是
A. B. C. D.
2. 若曲线表示椭圆,则k的取值范围是
A. B.
C. D. 或
3. 两平面,的法向量分别为,若,则的值是
A. B. 6 C. D.
4. 已知双曲线的离心率为,则椭圆的离心率为
A. B. C. D.
5. 已知双曲线的右焦点与抛物线的焦点重合,则该双曲线的焦点到其渐近线的距离等于
A. B. 3 C. 5 D.
6. 设双曲线的离心率是3,则其渐近线的方程为
A. B. C. D.
7. 设x,y满足约束条件,若取得最大值的最优解不唯一,则实数a的值为
A. 2或 B. 3或 C. 或 D. 或2
8. 设是直线l的方向向量,是平面的法向量,则直线l与平面
A. 垂直 B. 平行或在平面内
C. 平行 D. 在平面内
9. 数列,为等差数列,前n项和分别为,,若,则
A. B. C. D.
10. 已知A,B为抛物线E:上异于顶点O的两点,是等边三角形,其面积为,则p的值为
A. 2 B. C. 4 D.
1. 在长方体,,则异面直线与所成角的余弦值为
A. B. C. D.
2. 如图,分别是双曲线的左、右焦点,过的直线l与双曲线分别交于点,若为等边三角形,则双曲线的方程为
A.
B.
C.
D.
二、填空题(本大题共4小题,共20.0分)
3. 若抛物线的焦点在直线上,则此抛物线的标准方程是______ .
4. 三角形ABC中,角A,B,C所对边分别为a,b,c,已知,且,则三角形ABC外接圆面积为______.
5. 双曲线的渐近线与圆相切,则此双曲线的离心率为______.
6. 已知向量,,,,若,则的最小值______ .
三、解答题(本大题共6小题,共72.0分)
7. 已知不等式的解集为A,不等式的解集为B.
求;
若不等式的解集为,求a、b的值.
8. 在中,内角 A,B,C所对的边分别为a,b,c,且满足.
求角 A的大小;
若,求的面积.
9.
椭圆E:的一个焦点,离心率.
求椭圆E的方程;
求以点为中点的弦AB所在的直线方程.
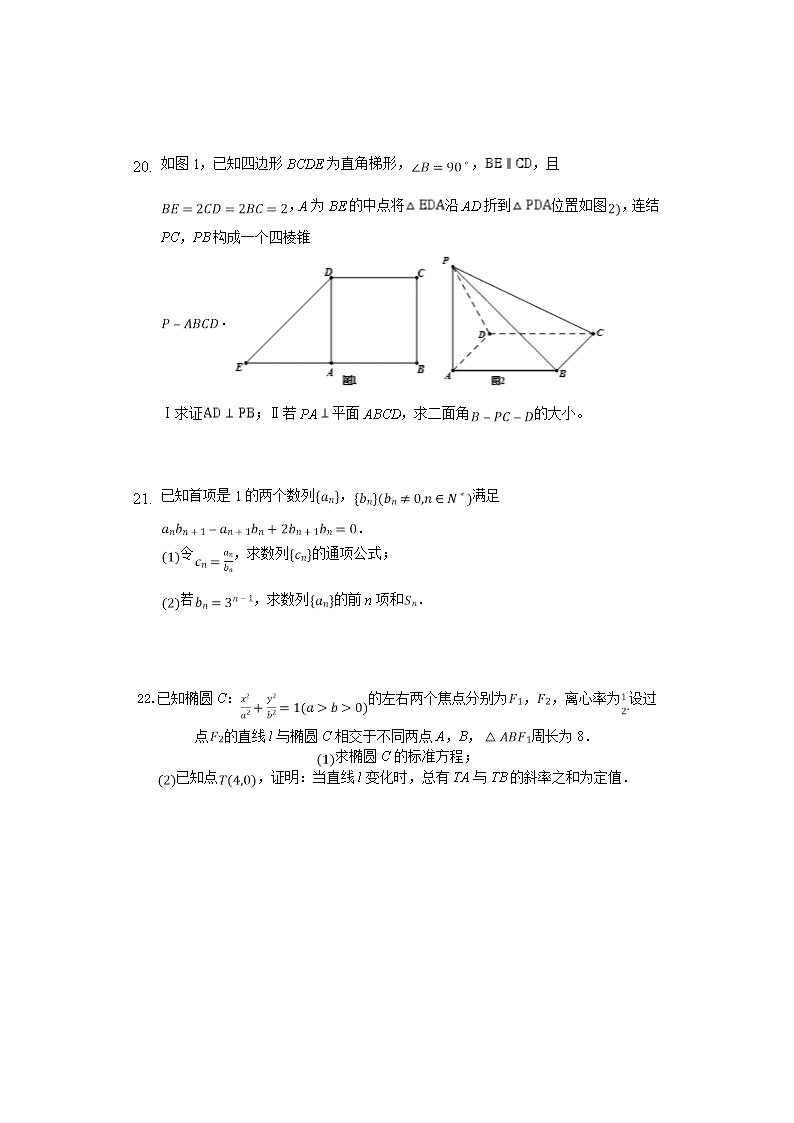
1. 如图1,已知四边形BCDE为直角梯形,,,且,A为BE的中点将沿AD折到位置如图,连结PC,PB构成一个四棱锥.
Ⅰ求证;Ⅱ若PA平面ABCD,求二面角的大小。
2. 已知首项是1的两个数列,满足.
令,求数列的通项公式;
若,求数列的前n项和.
22.已知椭圆C:的左右两个焦点分别为,,离心率为设过点的直线l与椭圆C相交于不同两点A,B,周长为8.
求椭圆C的标准方程;
已知点,证明:当直线l变化时,总有TA与TB的斜率之和为定值.
2018-2019学年度高二11月考数学试卷(理)
答案和解析
【答案】
1. C 2. D 3. B 4. C 5. A 6. A 7. A
8. B 9. A 10. A 11. B 12. C
13. 或
14.
15.
16.
17. 解:,
,
解得:,
,
,
,
解得:,
,
;
由得:,2为方程的两根,
,
.
18. 解:,
,
,
,
由余弦定理得,可得,
又,
.
根据正弦定理得,
又,
.
19. 解:设椭圆E的方程为,
由题意,又,得,
.
椭圆E的标准方程为;
设,代入椭圆E的方程得:
, ,
得:,
点为AB的中点,
.
即.
点为中点的弦AB所在直线的方程为,
化为一般式方程:.
20. 证明:Ⅰ在图1中,,,为平行四边形,,
,,当沿AD折起时,,,即,,
又,平面PAB,又平面PAB,;
Ⅱ以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,
则0,,0,,1,,0,,
1,,1,,0,,
设平面PBC的法向量为y,,
则,取,得0,,
设平面PCD的法向量b,,
则,取,得1,,设二面角的大小为,
则,二面角的大小为.
21. 解:,,
,
,
首项是1的两个数列,,
数列是以1为首项,2为公差的等差数列,
;
,,
,
,
,
,
.
22. 解:由题意知,,所以.
因为,所以,则.
所以椭圆C的方程为.
证明:当直线l垂直与x轴时,显然直线TA与TB的斜率之和为0,
当直线l不垂直与x轴时,设直线l的方程为,,,
,整理得:,
恒成立,
,,
由
,
由,
,
直线TA与TB的斜率之和为0,
综上所述,直线TA与TB的斜率之和为定值,定值为0.