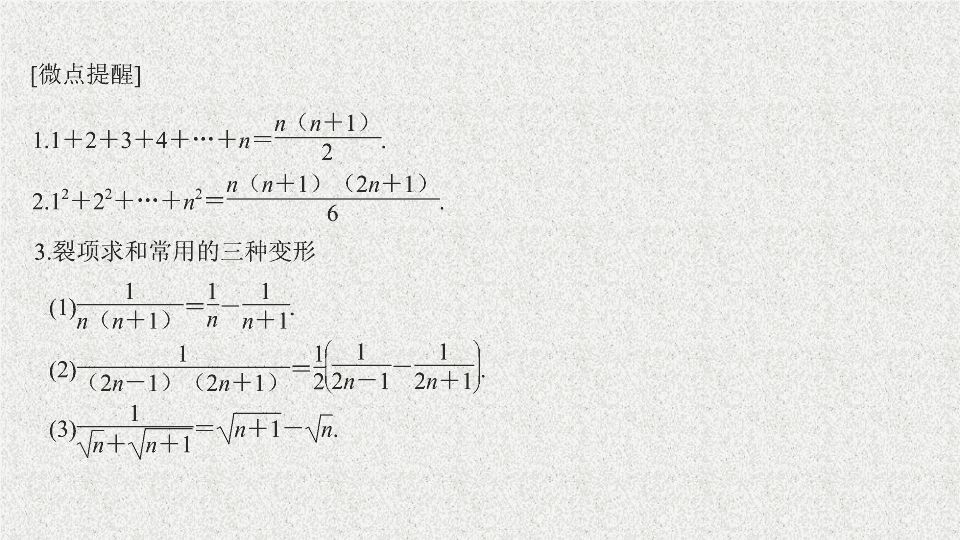2020届二轮复习数列求和课件（24张）（全国通用） 24页

知 识 梳 理 1. 特殊数列的求和公式 2. 数列求和的几种常用方法 (1) 分组转化法 把数列的每一项分成两项或几项，使其转化为几个等差、等比数列，再求解 . (2) 裂项相消法 把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和 . (3) 错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，这个数列的前 n 项和可用错位相减法求解 . (4) 倒序相加法 如果一个数列 { a n } 的前 n 项中与首末两端等 “ 距离 ” 的两项的和相等或等于同一个常数，那么求这个数列的前 n 项和即可用倒序相加法求解 . [ 微点提醒 ] 3. 裂项求和常用的三种变形 基 础 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) (3) 求 S n ＝ a ＋ 2 a 2 ＋ 3 a 3 ＋ … ＋ na n 时只要把上式等号两边同时乘以 a 即可根据错位相减法求得 .( 　　 ) 解析　 (3) 要分 a ＝ 0 或 a ＝ 1 或 a ≠ 0 且 a ≠ 1 讨论求解 . 答案　 (1) √ 　 (2) √ 　 (3) × 　 (4) √ A.2 018 B.2 019 C.2 020 D.2 021 答案　 B 4. (2018· 东北三省四校二模 ) 已知数列 { a n } 满足 a n ＋ 1 － a n ＝ 2 ， a 1 ＝－ 5 ，则 | a 1 | ＋ | a 2 | ＋ … ＋ | a 6 | ＝ ( 　　 ) A.9 B.15 C.18 D.30 解析 　由题意知 { a n } 是以 2 为公差的等差数列，又 a 1 ＝－ 5 ，所以 | a 1 | ＋ | a 2 | ＋ … ＋ | a 6 | ＝ | － 5| ＋ | － 3| ＋ | － 1| ＋ 1 ＋ 3 ＋ 5 ＝ 5 ＋ 3 ＋ 1 ＋ 1 ＋ 3 ＋ 5 ＝ 18. 答案 　 C 5. (2019· 榆林调研 ) 已知数列 { a n } ， { b n } 的前 n 项和分别为 S n ， T n ， b n － a n ＝ 2 n ＋ 1 ，且 S n ＋ T n ＝ 2 n ＋ 1 ＋ n 2 － 2 ，则 2 T n ＝ ________________. 解析　 由题意知 T n － S n ＝ b 1 － a 1 ＋ b 2 － a 2 ＋ … ＋ b n － a n ＝ n ＋ 2 n ＋ 1 － 2 ， 又 S n ＋ T n ＝ 2 n ＋ 1 ＋ n 2 － 2 ， 所以 2 T n ＝ T n － S n ＋ S n ＋ T n ＝ 2 n ＋ 2 ＋ n ( n ＋ 1) － 4. 答案　 2 n ＋ 2 ＋ n ( n ＋ 1) － 4 答案 　 a n ＝ 2( n ＋ 1) 考点一　分组转化法求和 【例 1 】 (2019· 郴州质检 ) 已知在等比数列 { a n } 中， a 1 ＝ 1 ，且 a 1 ， a 2 ， a 3 － 1 成等差数列 . (1) 求数列 { a n } 的通项公式； (2) 若数列 { b n } 满足 b n ＝ 2 n － 1 ＋ a n ( n ∈ N + ) ，数列 { b n } 的前 n 项和为 S n ，试比较 S n 与 n 2 ＋ 2 n 的大小 . 解　 (1) 设等比数列 { a n } 的公比为 q ， ∵ a 1 ， a 2 ， a 3 － 1 成等差数列， (2) 由 (1) 知 b n ＝ 2 n － 1 ＋ a n ＝ 2 n － 1 ＋ 2 n － 1 ， ∴ S n ＝ (1 ＋ 1) ＋ (3 ＋ 2) ＋ (5 ＋ 2 2 ) ＋ … ＋ (2 n － 1 ＋ 2 n － 1 ) ＝ [1 ＋ 3 ＋ 5 ＋ … ＋ (2 n － 1)] ＋ (1 ＋ 2 ＋ 2 2 ＋ … ＋ 2 n － 1 ) ∵ S n － ( n 2 ＋ 2 n ) ＝－ 1<0 ， ∴ S n < n 2 ＋ 2 n . 规律方法 　 1. 若数列 { c n } 的通项公式为 c n ＝ a n ± b n ，且 { a n } ， { b n } 为等差或等比数列，可采用分组求和法求数列 { c n } 的前 n 项和 . 【训练 1 】 (2019· 南昌一模 ) 已知等差数列 { a n } 的前 n 项和为 S n ，且 a 1 ＝ 1 ， S 3 ＋ S 4 ＝ S 5 . (1) 求数列 { a n } 的通项公式； (2) 令 b n ＝ ( － 1) n － 1 a n ，求数列 { b n } 的前 2 n 项和 T 2 n . 解　 (1) 设等差数列 { a n } 的公差为 d ， 由 S 3 ＋ S 4 ＝ S 5 可得 a 1 ＋ a 2 ＋ a 3 ＝ a 5 ，即 3 a 2 ＝ a 5 ， ∴ 3(1 ＋ d ) ＝ 1 ＋ 4 d ，解得 d ＝ 2. ∴ a n ＝ 1 ＋ ( n － 1) × 2 ＝ 2 n － 1. (2) 由 (1) 可得 b n ＝ ( － 1) n － 1 ·(2 n － 1). ∴ T 2 n ＝ 1 － 3 ＋ 5 － 7 ＋ … ＋ (2 n － 3) － (2 n － 1) ＝ ( － 2) × n ＝－ 2 n . 考点二　裂项相消法求和 (1) 求数列 { a n } 的通项公式； 规律方法 　 1. 利用裂项相消法求和时，应注意抵消后并不一定只剩下第一项和最后一项，也有可能前面剩两项，后面也剩两项 . 2. 将通项公式裂项后，有时候需要调整前面的系数，使裂开的两项之差和系数之积与原通项公式相等 . 【训练 2 】 设 S n 为等差数列 { a n } 的前 n 项和，已知 S 3 ＝ a 7 ， a 8 － 2 a 3 ＝ 3. (1) 求 a n ； 解　 (1) 设数列 { a n } 的公差为 d ， 解得 a 1 ＝ 3 ， d ＝ 2 ， ∴ a n ＝ a 1 ＋ ( n － 1) d ＝ 2 n ＋ 1. ∴ T n ＝ b 1 ＋ b 2 ＋ … ＋ b n － 1 ＋ b n 考点三　错位相减法求和 【例 3 】 已知 { a n } 是各项均为正数的等比数列，且 a 1 ＋ a 2 ＝ 6 ， a 1 a 2 ＝ a 3 . (1) 求数列 { a n } 的通项公式； 解　 (1) 设 { a n } 的公比为 q ， 又 S 2 n ＋ 1 ＝ b n b n ＋ 1 ， b n ＋ 1 ≠ 0 ，所以 b n ＝ 2 n ＋ 1. 规律方法 　 1. 一般地，如果数列 { a n } 是等差数列， { b n } 是等比数列，求数列 { a n · b n } 的前 n 项和时，可采用错位相减法 . 2. 用错位相减法求和时，应注意： (1) 要善于识别题目类型，特别是等比数列公比为负数的情形 . (2) 在写出 “ S n ” 与 “ qS n ” 的表达式时应特别注意将两式 “ 错项对齐 ” ，以便于下一步准确地写出 “ S n － qS n ” 的表达式 . (1) 求数列 { b n } 的通项公式； (2) 若 c n ＝ 2 a n ·( b n － 1)( n ∈ N + ) ，求数列 { c n } 的前 n 项和 T n . 解 　 (1) 当 n ＝ 1 时， a 1 ＝ S 1 ＝ 1 ； 又 a 1 ＝ 1 符合上式， ∴ a n ＝ n ( n ∈ N + ) ， ∴ b n ＝ a n ＋ a n ＋ 1 ＝ 2 n ＋ 1.