- 87.50 KB
- 2021-04-17 发布
12.3互逆命题(2)
【学习目标】在证明中,不断发展合乎逻辑的思考、有条理的表达能力。
【预习研问】
1A你能说出两个命题:它们不仅是互逆命题,而且都是真命题吗?
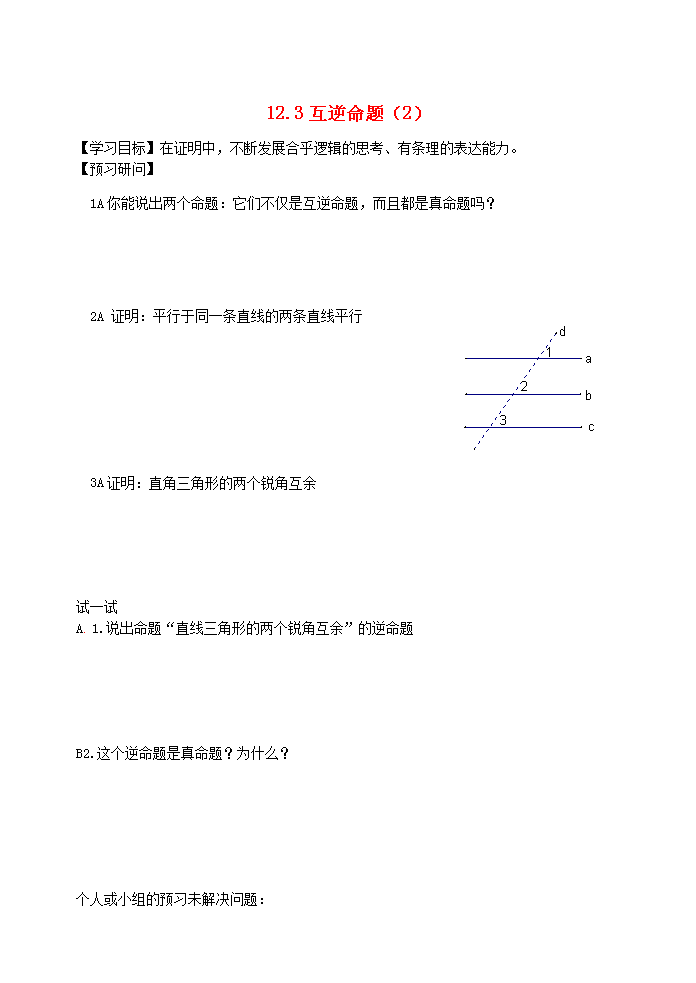
2A 证明:平行于同一条直线的两条直线平行
3A证明:直角三角形的两个锐角互余
试一试
A 1.说出命题“直线三角形的两个锐角互余”的逆命题
B2.这个逆命题是真命题?为什么?
个人或小组的预习未解决问题:
【课内解问】
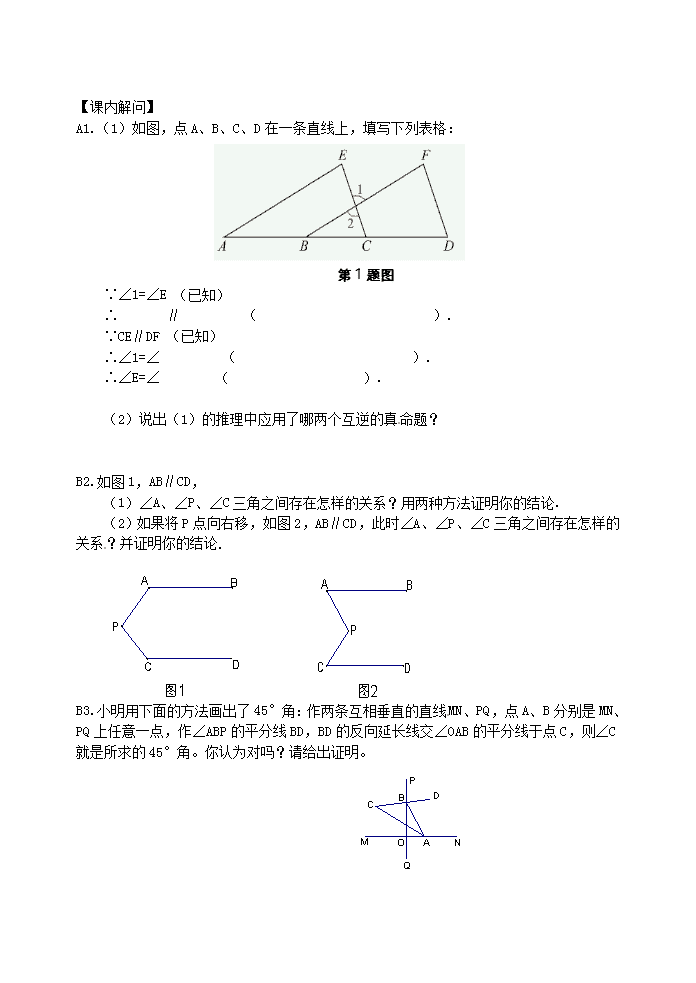
A1.(1)如图,点A、B、C、D在一条直线上,填写下列表格:
第1题图
∵∠1=∠E (已知)
∴ ∥ ( ).
∵CE∥DF (已知)
∴∠1=∠ ( ).
∴∠E=∠ ( ).
(2)说出(1)的推理中应用了哪两个互逆的真命题?
B2.如图1,AB∥CD,
(1)∠A、∠P、∠C三角之间存在怎样的关系?用两种方法证明你的结论.
(2)如果将P点向右移,如图2, AB∥CD,此时∠A、∠P、∠C三角之间存在怎样的关系?并证明你的结论.
B3.小明用下面的方法画出了45°角:作两条互相垂直的直线MN、PQ,点A、B分别是MN、PQ上任意一点,作∠ABP的平分线BD,BD的反向延长线交∠OAB的平分线于点C,则∠C就是所求的45°角。你认为对吗?请给出证明。
【课后答问】
A1..给下面的证明过程证明理由
已知AB=DC,∠BAD=∠CDA
求证:∠ABC=∠DCB
证明:连结AC、BD交点为O
在△ADB与△DAC中
因为∠BAD=∠ADC ( )
AD=DA ( )
AB=DC ( )
所以△ADB≌△DAC ( )
所以BD=CA
又在△ABC与△DCB中
因为BD=CA ( )
AB=DC ( )
BC=BC ( )
所以△ABC≌△DCB ( )
所以∠ABC=∠DCB
C
B
E
D
A
A 2.已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C。
求证:AD平分∠EAC。
B3.如图,在△ABC中,(1)P是△ABC内任意一点,∠BPC与∠A有怎样的大小关系?证明你的结论。(2)如果BP、CP分别平分∠ABC、∠ACB: ①已知∠A=60°,求∠BPC的度数; ②已知∠A= n°,求∠BPC的度数.
B
C
A
P
B4. 探索两个连续奇数的平方差的规律,并加以证明。
相关文档
- 数学(心得)之初中数学反思性学习能力2021-04-17 09:49:534页
- 2019-2020学期人教版初中数学7-9年2021-04-17 09:25:2311页
- 青岛初中数学七年级上册生活中的常2021-04-17 09:13:488页
- 青岛初中数学七年级上册《2 数轴》2021-04-17 02:51:4117页
- 数学计划总结之初中数学教学工作总2021-04-17 01:46:525页
- 新人教版初中数学年级下册章精品导2021-04-17 00:36:3628页
- 2020人教版初中数学八年级上册知识2021-04-17 00:24:4660页
- 精编初中数学老师心得2021-04-16 23:34:5813页
- 初中数学青岛九上期中数学试卷2021-04-16 22:59:0510页
- 2020初中数学教师个人期末工作总结2021-04-16 22:52:239页