2017-2018学年湖北省武汉市卓刀泉中学九年级数学12月月考 6页

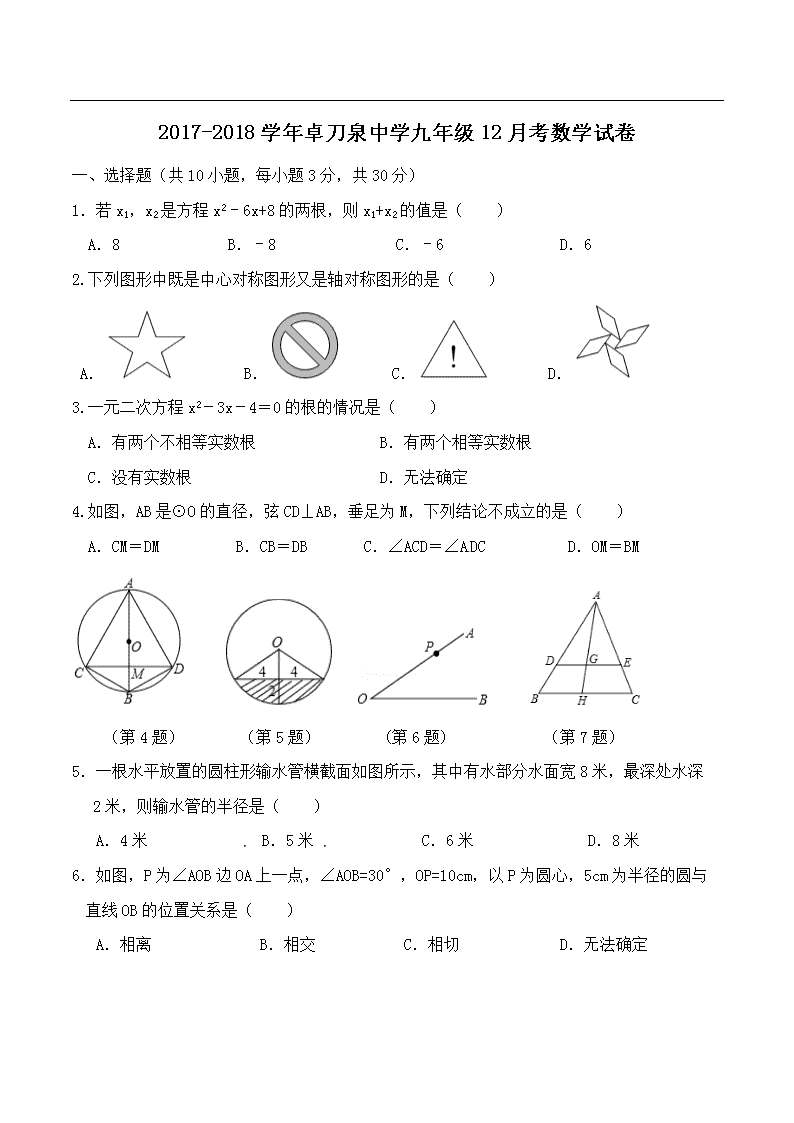
‎2017-2018学年卓刀泉中学九年级12月考数学试卷 一、选择题（共10小题，每小题3分，共30分）‎ ‎1．若x1，x2是方程x2﹣6x+8的两根，则x1+x2的值是（　　）‎ A．8 B．﹣8 C．﹣6 D．6‎ ‎2.下列图形中既是中心对称图形又是轴对称图形的是（　　）‎ A． B． C． D．‎ ‎3.一元二次方程x2－3x－4＝0的根的情况是（ ）‎ A．有两个不相等实数根 B．有两个相等实数根 C．没有实数根 D．无法确定 ‎4.如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（ ）‎ A．CM＝DM B．CB＝DB C．∠ACD＝∠ADC D．OM＝BM ‎ ‎ ‎ ‎ （第4题） （第5题） (第6题) （第7题）‎ ‎5．一根水平放置的圆柱形输水管横截面如图所示，其中有水部分水面宽8米，最深处水深 ‎2米，则输水管的半径是（　　）‎ A．4米 B．5米 C．6米 D．8米 ‎6．如图，P为∠AOB边OA上一点，∠AOB=30°，OP=10cm，以P为圆心，5cm为半径的圆与 直线OB的位置关系是（　　）‎ A．相离 B．相交 C．相切 D．无法确定 ‎7. 如图，△ABC中，，且DE＝12，BC＝15，GH＝4，则AH的长为（ ）‎ A．12 B．16 C．20 D． 24‎ ‎8. 要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（　　）‎ A．x（x+1）=28 B．x（x﹣1）=28 ‎ ‎ C．x（x+1）=28 D．x（x﹣1）=28‎ ‎9．已知二次函数y=﹣（x+h）2，当x＜﹣3时，y随x增大而增大，当x＞0时，y随x增大而减小，且h满足h2﹣2h﹣3=0，则当x=0时，y的值为（　　）‎ A．﹣1 B．1 C．﹣9 D．9‎ ‎10. 如图，在△ABC中，AC＝3，BC＝，∠ACB＝45°，AM∥BC，点P在射线AM上运动，‎ 连BP交△APC的外接圆于D，则AD的最小值为（ ）‎ A．1 B．2 C． D．‎ 二、填空题（本大题共6个小题，每小题3分，共18分）‎ ‎11．半径为4的正六边形的边心距为 ，中心角等于 ，面积为 ．‎ ‎12．已知点O为△ABC的外心，且∠BOC=80°，则∠BAC=　 　. 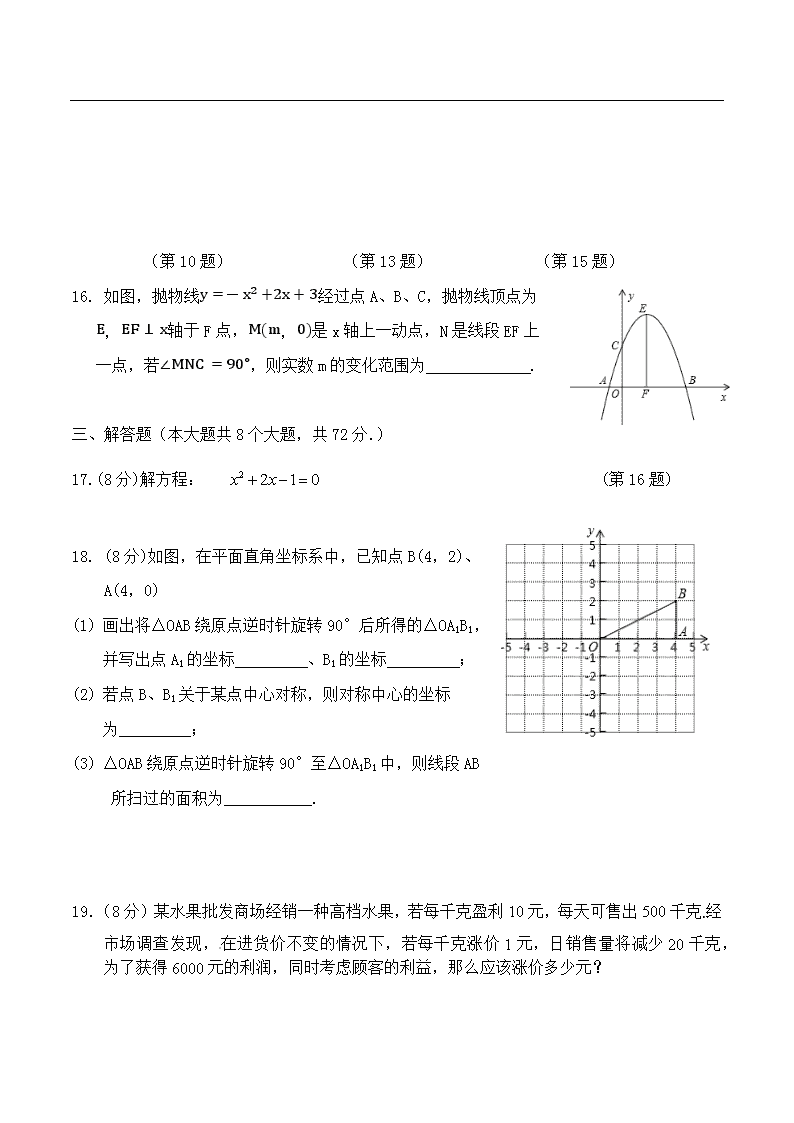‎ ‎13．如图，对称轴平行于y轴的抛物线与x轴交于（1，0），（3，0）两点，则它的对称轴为　 　.‎ ‎14．一个圆锥的侧面积是底面积的3倍，则它的侧面展开图的圆心角的度数为___________.‎ ‎15．如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，则水面下降1m时，水面宽度 增加 m.‎ ‎[来源:学&科&网]‎ ‎[来源:Z*xx*k.Com]‎ ‎ （第10题） （第13题） （第15题）‎ ‎16. 如图，抛物线y=-x‎2‎+2x+3‎经过点A、B、C，抛物线顶点为 ‎ E，EF⊥x轴于F点，M(m，0)‎是x轴上一动点，N是线段EF上 一点，若‎∠MNC=‎‎90‎‎∘‎，则实数m的变化范围为 . ‎ ‎ ‎ 三、解答题（本大题共8个大题，共72分．）‎ ‎17.(8分)解方程： (第16题) [来源:Z+xx+k.Com]‎ ‎18. (8分)如图，在平面直角坐标系中，已知点B(4，2)、‎ A(4，0)‎ (1) 画出将△OAB绕原点逆时针旋转90°后所得的△OA1B1，‎ 并写出点A1的坐标 、B1的坐标 ；‎ (2) 若点B、B1关于某点中心对称，则对称中心的坐标 为_________；‎ (3) ‎△OAB绕原点逆时针旋转90°至△OA1B1中，则线段AB 所扫过的面积为___________.‎ ‎19．（8分）某水果批发商场经销一种高档水果，若每千克盈利10元，每天可售出500千克‎.‎经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克， 为了获得6000元的利润，同时考虑顾客的利益，那么应该涨价多少元？‎ ‎20.（8分）如图，直线y=x+m和抛物线y=x2+bx+c都经过点A（1，0），B（3，2）． （1）求m的值和抛物线的解析式； ‎ ‎（2）求不等式x2+bx+c≥x+m的解集．（直接写出答案）‎ ‎21.(8分) 如图，Rt△ABC中，∠C=90°，BC=9，CA=12，∠ABC的平分线BD交AC于D点，‎ DE⊥DB交AB于点E．‎ ‎（1）设⊙O是△BDE的外接圆，试说明AC是⊙O的切线；‎ ‎（2）设⊙O交BC于点F，连接EF，求 的值．‎ ‎22.（本题10分）如图，正方形ABCD的边长是4，E是AB边上一点（E不与A、B重合），‎ F是AD的延长线上一点，DF=2BE．四边形AEGF是矩形，矩形AEGF面积y随BE的长x的变化而变化且构成函数．[来源:学科网ZXXK]‎ ‎（1）求y与x之间的函数关系式，并写出自变量x的取值范围；‎ ‎（2）当x取何值时，y取得最大（或最小）值，该值是多少？‎ ‎（3）若矩形AEGF的面积是10，求BE的长． ‎ ‎23.（10分）四边形ABDF中，点C、E分别在AF、DF上，且AB=AC，BD=DE，∠BDF=2∠ABC,‎ M为CE的中点．‎ ‎（1）画出△ACM关于点M成中心对称的图形；‎ ‎（2）求证：AM⊥DM；‎ ‎（3）若AM=DM，求∠ABC的度数.‎ ‎[来源:学科网ZXXK]‎ ‎24.（12分）如图，平面直角坐标系中，抛物线y=x‎2‎-2x与x轴交于O、B两点，顶点为P，连接OP、BP，直线y=x-4‎与y轴交于点C，与x轴交于点D． ‎(‎Ⅰ‎)‎直接写出点B坐标 ；判断‎△OBP的形状 ； ‎(‎Ⅱ ‎)‎将抛物线沿对称轴平移m个单位长度，平移的过程中交y轴于点A，分别连接CP、DP； ‎(i)‎若抛物线向下平移m个单位长度，当S‎△PCD‎=‎‎2‎S‎△POC时，求平移后的抛物线的顶点 坐标； ‎(ii)‎在平移过程中，试探究S‎△PCD和S‎△POD之间的数量关系，直接写出它们之间的数量关系 及对应的m的取值范围． ‎ ‎ ‎