- 1.35 MB
- 2021-04-17 发布
哈尔滨市第六中学2019-2020学年度上学期期中考试
高二理科数学试题
一.选择题(每题5分,共60分)
1.已知双曲线的渐近线为,实轴长为,则该双曲线的方程为( )
A. B.或
C. D.或
2.给出以下几个结论:
(1)垂直于同一直线的两条直线互相垂直;
(2)垂直于同一平面的两个平面互相平行;
(3)若,是两个平面,,是两条直线,且,,,,则;
(4)若 ,是两个平面,,是两条直线,,则
(5)若,是两个平面,,是两条直线,,则
其中错误结论的个数为( )
A.2 B.3 C.4 D. 5
3.已知一个三棱锥的高为,其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为的等腰直角三角形(如右图所示),则此三棱锥的体积为( )
A. B. C. D.
4.长方体平面与长方体的各个面所形成的二面角的大小中不正确的有( )
A. B. C. D.
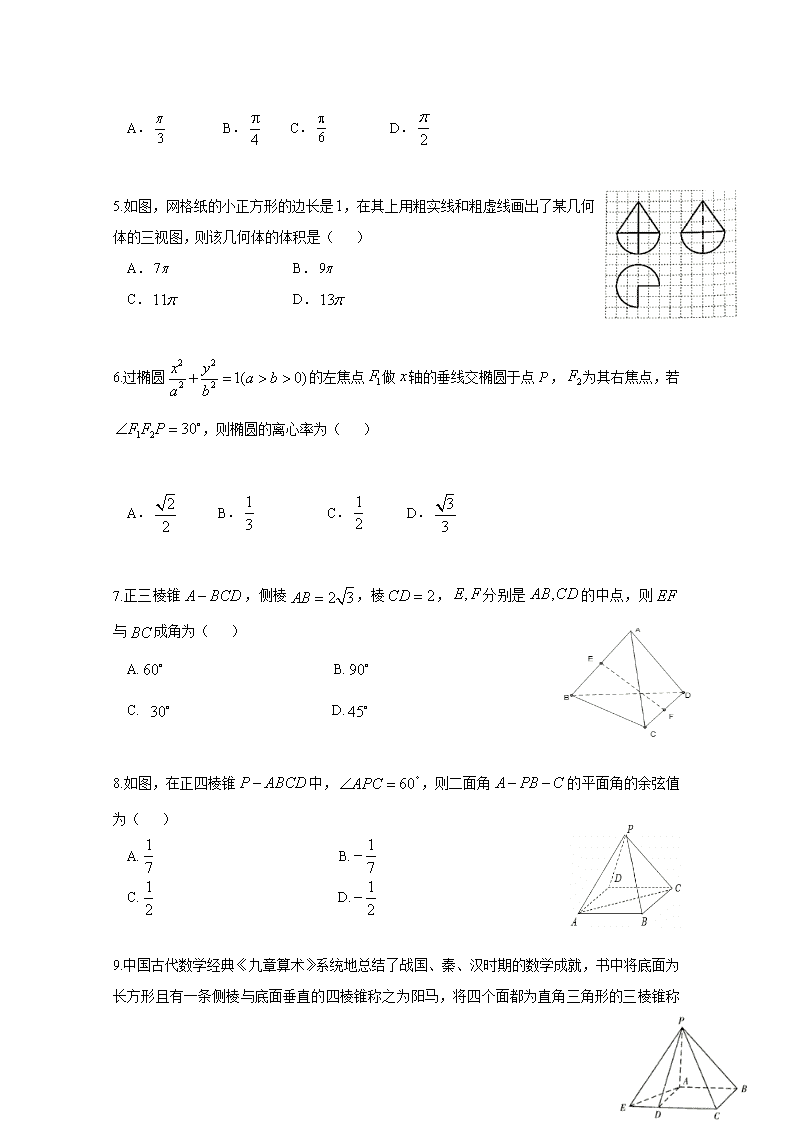
5.如图,网格纸的小正方形的边长是,在其上用粗实线和粗虚线画出了某几何体的三视图,则该几何体的体积是( )
A. B.
C. D.
6.过椭圆的左焦点做轴的垂线交椭圆于点,为其右焦点,若,则椭圆的离心率为( )
A. B. C. D.
7.正三棱锥,侧棱,棱,分别是的中点,则与成角为( )
A. B.
C. D.
8.如图,在正四棱锥中,,则二面角的平面角的余弦值为( )
A. B.
C. D.
9.
中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑.如图为一个阳马与一个鳖臑的组合体,已知平面,四边形为正方形,,,若鳖臑的体积为1,则阳马的外接球的表面积等于( )
A. B. C. D.
10.在四面体中,底面,,
为的重心, 为线段的一点,且平面,则线段的长度是( )
A. B. C. D.
11.如图,在正方体中,是棱上的动点.下列说法正确的是( )
A.对任意动点在平面内不存在与平面平行的直线
B.对任意动点在平面内存在与平面垂直的直线
C.当点从运动到的过程中,点到平面的距离逐渐变大
D.当点从运动到的过程中,二面角的大小不变
12.已知椭圆C的焦点为,过的直线与C交于A,B两点.若,,则C的方程为( )
A. B. C. D.
二.填空题(共20分)
13.双曲线上的一点到它的一个焦点的距离等于1,那么点到另一个焦点的距离为___________________
14. 某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为___________
15.已知圆锥的底面半径为1,高为,点是底面圆周上一点,若一动点从点出发,绕圆锥侧面一圈之后回到点,则绕行的最短距离为_________________
16. 对于四面体,给出下列四个命题:
①若,,则;
②若,则点在平面内的射影为的重心;
③若,,则;
④若,,则.
⑤若,则点在平面内的射影为的外心
其中真命题的序号是________.
三.解答题(共70分)
17.(共10分)如图,在正方体中,为的中点.
(1)求证:平面;
(2)求证:平面平面
18.(共12分)如图,在四棱锥中,底面是菱形,,侧面为正三角形,且平面平面.
(1)求证:.
(2)若为中点,试在上找一点,使平面平面.
19. (共12分)如图,在正方体中,分别是的中点。
(1)求异面直线与所成角的余弦值;
(2)棱上是否存在点,使得平面?请证明你的结论。
20.(共12分)如图,在四棱锥中,底面为菱形,,点为的中点,且.
(1)求证: 平面;
(2)若,求平面与平面所成二面角的余弦值;
(3)在第(2)问的前提下,求直线与平面所成角的正弦值.
21.(共12分)设抛物线的焦点为
(1)过且斜率为的直线与抛物线交于,两点, .求的方程;
(2)若斜率为的直线与抛物线的交点为,与轴的交点为.若,求线段的长度.
22. (共12分)在平面直角坐标系中,动点与两定点连线的斜率之积为,记点的轨迹为曲线
(1)求曲线的方程;
(2)若过点的直线与曲线交于两点,曲线上是否存在点使得四边形为平行四边形?若存在,求直线的方程,若不存在,说明理由;
(3)过坐标原点的直线交于两点,点在第一象限,轴,垂足为,连结并延长交于点. 证明:是直角三角形.
高二理科数学答案
一.选择题
1
2
3
4
5
6
7
8
9
10
11
12
B
C
B
B
C
D
A
B
A
B
D
D
二.填空题
13. 17 14.3 15. 16. ①④⑤
17. (Ⅰ) 令,连接,
则四边形是平行四边形,
;又是的中点
,则四边形是平行四边形,
,
所以 平面;
(2)证明平面,平面,平面平面
18.(1)证明:取的中点,连接
,.在底面菱形中,
,,则平面,
(2)为的中点,连接交于点.
,,为的中点,
则.平面平面,,平面,
则平面,平面平面.设正方体棱长为
则,,,,,,,
19.(1)设异面直线与所成角为,
,即异面直线与所成角的余弦值为:
(2)假设在棱上存在点,,使得平面
则,,
设平面的法向量
,令,则,
,解得:
棱上存在点,满足,使得平面
20.(1)证明:连结OP,BD,因为底面ABCD为菱形,,
故,又O为AD的中点,故.
在中,,O为AD的中点,所以.
设,则,,
因为,
所以.(也可通过来证明),
又因为,平面PAD,平面PAD,
所以平面PAD;
(2)因为,,
,平面POB,平面POB,
所以平面POB,又平面POB,所以.
由(1)得平面PAD,又平面PAD,故有,又由,
所以OA,OB,OP所在的直线两两互相垂直.
故以O为坐标原点,以OA,OB,OP所在直线为x轴,y轴,z轴如图建系.
设,则,,,.
所以,,,
由(1)知平面PAD,
故可以取与平行的向量作为平面PAD的法向量.
设平面PBC的法向量为,则,
令,所以.
设平面PBC与平面PAD所成二面角为θ,则,
(3)所以直线平面PBC所成线面角的正弦值为.
21.(1)设A(x1,y1),B(x2,y2).
由得. ,故.
所以.
由题设知,解得,k=–1(舍去),k=1.因此l的方程为y=x–1.
(2),得,则
, , 则
22. 解:(Ⅰ)设P(x,y),有·=-
得·=-整理得=1(x≠±2)
∴曲线C的方程为=1(x≠±2)
(II)假设存在符合条件的点E()由题意知直线l的斜率不为零
设直线l的方程为x=my-
点M坐标为()、点N坐标为()
由得:(+2)-2my-3=0,△>0
∴+则+=-
由四边形OMEN为平行四边形,得到
∴E(-)把点E坐标代入曲线C的方程得:=0,解得
∴此时直线l的方程为,但,所以不存在.
(3)(3) 设直线的方程为,由题意可知,直线的方程与椭圆方程联立,即或,点P在第一象限,所以,因此点的坐标为
直线的斜率为,可得直线方程:,与椭圆方程联立,,消去得,(*),设点,显然点的横坐标和是方程(*)的解
所以有,代入直线方程中,得
,所以点的坐标为,
直线的斜率为; ,
因为所以,因此是直角三角形;