一元一次方程复习和实际问题人教版七年级上 130页

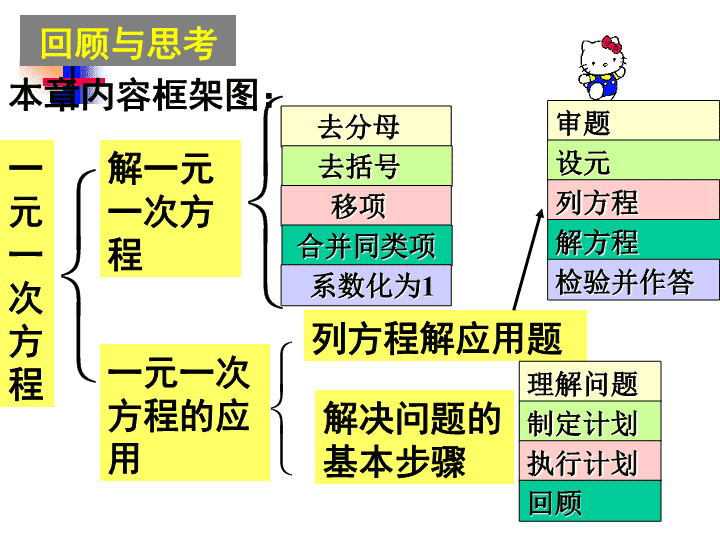
第三章 一元一次方程复习 回顾与思考 本章内容框架图： 一元一次方程 解一元一次方程 一元一次方程的应用 去分母 去括号 移项 合并同类项 系数化为 1 列方程解应用题 审题 设元 列方程 解方程 检验并作答 解决问题的基本步骤 理解问题 制定计划 执行计划 回顾 什么叫方程？ 含有未知数的等式叫做 方程 。 注意： 判断一个式子是不是方程，要看两点： 一是等式；二是含有未知数。 二者缺一不可。 知识 回顾 想一想 1 判断下列各式哪些是方程，哪些不是？ 为什么？ 否 是 否 是 是 是 1 、 3-2=1 2 、 5x-1=9 3 、 y=0 4 、 x 2 +2x+1 5 、 3x-y=0 6 、 x 2 =5x-6 试一试 1 典例分析 1 方程的基本变形法则 ( 等式基本性质 ) 是什么？ (1) 方程两边都加上或都减去同一个 数或同一个整式，方程的解不变 . （2）方程两边都乘以或都除以同一个不为零的数，方程的解不变。 想一想 2 什么叫方程的解？ 使方程左右两边的值相等的 未知数的值叫做 方程的解 . 求方程的解的过程叫 解方程 。 想一想 3 什么叫移项？ 将方程中的某些项改变符号后，从 方程的一边移到另一边的变形叫做 移项 。 ※注意：移项一定要变号。 想一想 4 大家判断一下，下列方程的变形是否正确？ 为什么？ （1） （2） （3） （4） （×） （×） （×） （×） 试一试 2 典例分析 2 1.什么是一元一次方程？ 2.一元一次方程的一般式是什么？ 只含有一个未知数，并且含有未知数 的式子都是整式，未知数的次数是1，这样 的方程叫做一元一次方程. ax+b=0 ( a ≠0 , a、b 为常数 ） 想一想 5 1.判断下列方程是否为一元一次方程？ 为什么？ （1） （5） （3） （4） （2） （6） 否 否 否 否 是 是 试一试 3 典例分析 3 2. 若 是一元一次方程， 则 。 3. 若方程 是一元一次 方程，则 应满足 。 4. 若 是方程 的解，则代数式 。 2 1 a≠3 试一试 3 3. 如果单项式 与 是同类项，那么 m= , n= . 4. 如果 是关于 X 的一元一次方程，则 a= 解一元一次方程的一般步骤是什么？ （1）去分母 （2）去括号 （3）移项 （4）合并同类项 （5）系数化为1 ①不能漏乘不含分母的项。 ② 分子是多项式时应添括号。 ①不要漏乘括号内的任何项。 ② 如果括号前面是“－”号， 去括号后括号内各项变号 。 ①从方程的一边移到另一边 注意变号。 ①把方程一定化为 ax = b (a≠0) 的形式 ②系数相加，字母及其指数不变。 ①方程两边除以未知数的系数。 ②系数只能做分母，注意不要颠倒。 想一想 6 解： 试一试 4 典例分析 4 解： 变式 变式训练 1 解： 变式 变式训练 2 用适当的方法解下列方程 能力训练 练一练 解： 解： ＝ 3 变式 变式训练 3 方程的定义 方程的基本变形法则 方程 移项 一元一次方程 一元一次方程的概念 解一元一次方程的一般步骤 一元一次方程的标准式 方程的解 ax+b=0 (a ≠0 , a、b 为常数 ） 畅所欲言 回味无穷 1 中考链接 1 1. （ 2010. 怀化）已知关于 x 的方程 3x-2m=4 的解是 x=m ，则 m 的值是 ． 2. （ 2010. 宿迁市）已知 5 是关于 x 的方程 　　 3x-2 a =7 的解，则 a 的值为 ． 4 4 自我展示 1. 下列方程中属于一元一次方程的是（ ） A y 2 =4 B 2+ =0 C x 2 +x+1=0 D x-2y=1 2. 下列方程的解是 2 的是（ ） A. x+5=1-2x B. 5x-3=0 C.x-2=0 D. x-2y=1 3. 如果 2x a+1 +3=0 是关于 x 的一元一次方程，则 - a 2 +2a 的值是（ ） A. 0 B. 2 C. 3 D. 4 4. 解方程： 4(x+0.5)=x+7 解：去括号得： 4X+2=X+7 移项得： 4X-X=7-2 合并得： 3X=5 系数化为 1 ： X= B C A 当堂测试 1 试一试 1. 解： 2. 解： 论字母系数吗？ 这道题需要讨 拿到含字母系数的方程首先分析字母系数的性质。 2.若方程 与方程 的解相同，则 a = 。 。 1.若两个多项式 与 的值 互为相反数，则 的值是 －6 2 挑战自我 1. 若关于 的方程 是 一元一次方程，求这个方程的解. 解：根据题意可知， ∴ 即 又∵ ∴ ∴ 当 m =－2 时，原方程为 解得 ， 拓展思维 独立 作业 解一元一次方程的一般步骤 变形名称 注意事项 去分母 去括号 移项 合并同类项 (ax=b) 方程两边同除以未知数的系数 a 防止漏乘（尤其整数项），注意添括号 ； 注意变号，防止漏乘； 移项要变号，防止漏项； 计算要仔细，不要出差错； 计算要仔细，不要出差错； 工程问题 一元一次方程的应用 1 、一批零件，甲每小时能加工 80 个，则 　　 ⑴ 甲 3 小时可加工　　个零件， x 小时可加工　　个零件。 ⑵ 加工 a 个零件，甲需　　　　小时完成。 2 、一项工程甲独做需 6 天完成，则 ⑴ 甲独做一天可完成这项工程的 ⑵ 若乙独做比甲快 2 天完成，则乙独做一天可完成 　这项工程的 240 80x 做一做 工程问题的基本数量关系： 工作总量 = 工作时间 × 工作效率 当不知道总工程的具体量时，一般把总工程当做“ 1” ，如果一个人 单独完成 该工程需要 a 天，那么该人的工作效率是 1/a 工程问题中的数量关系： 1 ） 工作效率 = 工作总量 完成工作总量的时间 ——————————— 2 ）工作总量 = 工作效率 × 工作时间 3 ）工作时间 = 工作总量 ————— 工作效率 4 ）各队合作工作效率 = 各队工作效率之和 5 ）全部工作量之和 = 各队工作量之和 例 1: 甲每天生产某种零件 80 个，甲生产 3 天 后，乙也加入生产同一种零件，再经过 5 天， 两人共生产这种零件 940 个，问乙每天生产 这种零件多少个？ 拿来用 分析 解题 头 3 天甲生产 零件的个数 甲乙后 5 天生产零件的总个数 甲后 5 天生 产的个数 乙后 5 天生 产的个数 940 个 图示 相等关系 头 3 天甲 生产零件 的个数 + 后 5 天甲 生产零件 的个数 后 5 天乙 生产零件 的个数 + = 940 例 2 、一件工作，甲单独做 20 个小时完成，乙单独做 12 小时完成，现在先由甲单独做 4 小时，剩下的部分由甲、乙合做。剩下的部分需要几小时完成？ 　左边 　　　　　右边 全部工作量“ 1” 甲先做 4 小时完成的工做量 合做 x 小时甲完成的工作量 合做 x 小时乙完成的工作量 相等关系：全部工作量＝甲独做工作量＋甲、乙合作工作量 全部工作量为“ 1” 设甲、乙合做部分需要 x 小时完成，甲独做部分完成的工作量为 甲、乙合做部分完成的工作量为 工程问题基本等量关系： 每个人的工作量之和 = 一共完成的工作量 解： 设剩下的部分需要 x 小时完成，根据题意，得 解这个方程，得 x=6 答：剩下的部分需要 6 小时完成。 　注意：工作量 = 工作效率 × 工作时间 例 2 、一件工作，甲单独做 20 个小时完成，乙单独做 12 小时完成，现在先由甲单独做 4 小时，剩下的部分由甲、乙合做。剩下的部分需要几小时完成 ？ 课练： 练习 1 、某工作由甲、乙两队单独做分别需要 3 小时、 5 小时，求两人合做这项工作的 80% 需要几小时？ 解：设两人合做这项工做需 x 小时，根据题意得， 　　　　　 (1/3 ＋ 1/5)x=80% 解这个方程得　 　　　　　　　 x=3/2 答：两人合做这项工做的 80% 需 3/2 小时。 例题讲解 例 3 挖一条长为 1210 米长的水渠，由甲施工队独做需要 11 天完成，乙施工队独做需要 20 天完成，现在甲、乙两 施工队从两头同时施工，挖完这条水渠估计需几天？ 等量关系： 甲施工队挖的米数 + 乙施工队挖的米数 =1210 米 答：两个施工队合作估计需要八天挖完。 解：设挖完这条水渠估计要 x 天 . 依题意得 x ≈8 分析：把这个问题看成工程问题的话， 通常把总量（即本题中的这条水渠）看成“ 1” ， 由题意得： 例题讲解 例 3 挖一条长为 1210 米长的水渠，由甲施工队独做需要 11 天完成，乙施工队独做需要 20 天完成，现在甲、乙两 施工队从两头同时施工，挖完这条水渠估计需几天？ 即本题的等量关系为 例 1 中的 1210 这个数据可以不用，解方程也简单。 甲完成工作量 + 乙完成工作量 =1 x ≈8 解：设挖完这条水渠估计要 x 天 . 例 4 修筑一条公路，甲工程队单独承包要 80 天完成，乙工程队单独 承包要 120 天完成 1 ）现在由两个工程队合作承包，几天可以完成？ 2 ）如果甲、乙两工程队合作了 30 天后，因甲工作队另有任务， 剩下工作由乙工作队完成，则修好这条公路共需要几天？ 解： 1 ）设两工程队合作需要 x 天完成。 2 ）设修好这条公路共需要 y 天完成。 等量关系： 甲 30 天工作量 + 乙队 y 天的工作量 = 1 答：两工程队合作需要 48 天完成，修好这条公路还需 75 天。 等量关系：甲工作量 + 乙工作量 =1 依题意得 依题意得 y=75 x=48 依题意得： x=10 答：两管同时注油 10 小时可注满油轮的 例 5 等量关系：甲管注油量 + 乙管注油量 = 解：设两管同时注油需 x 小时可注满油轮的 例 6 、 已知开管注水缸， 10 分钟可满，拨开底塞，满缸水 20 分钟流完，缸内的水流完后，现若管、塞同开，若干时间后，将底塞塞住，又过了 2 倍的时间才注满水缸，求管塞同开的时间是几分钟？ 分析： 注入或放出率 注入或放出时间 注入或放出量 注入 放出 解：设两管同开 x 分钟 等量关系：注入量－放出量 = 缸的容量 依题意得： x=4 答：管塞同开的时间为 4 分钟 x+2x=3x （分钟） x （分钟） 解：设再经过 x 小时水槽里的水恰好等于水槽的 等量关系：甲管流进水的水 + 乙管流出的水 = 水槽的 依题意得： ， 例 7 、 一 个 水 槽 有 甲 、 乙 两 个 水 管 。 甲 水 管 是 进 水 管， 在 5 小 时 之 内 可 以 把 空 水 槽 装 满 。 乙 水 管 是 出 水 管 ， 满 槽 的 水 在 6 小 时 内 可 以 流 完 。现水槽内没水， 如 果 先 开 甲 水 管 1 小 时 ， 再 把 乙 水 管 也 打 开 ， 再 经 过 几 小 时 5 水 槽 里 的 水 恰 好 等 于 水 槽 容 量 的 ？ 18 答：再经过 小时水槽里的水恰好是水槽容量的 3. 一收割 机队每天收割小麦 12 公顷 , 收割完一片麦地的 后 , 该收割机改进操作 , 效率提高到原来的 倍 , 因此比预定时间提早 1 天完成 . 问这片麦地 有多少公顷 ? 　　　　　　　　　　　　　　　　　 解 : 设这片麦地 有 X 公顷 , 由题意得 检验 :x=180 适合方程，且符合题意． 答：这片麦地 有１８０公顷 课后习题 某装潢公司接到一项业务，如果由甲组需 10 天完成，由乙组做需 15 天完成 . 为了早日完工，现由甲、乙两组一起做， 4 天后甲组因另有任务，余下部分由乙组单独做，问还需几天才能完成？ 动脑动笔 ？ 带着问题 (1) 可否用示意图来分析数量关系 ? (2) 总工作量怎么表示 ? 甲乙两人的工作 效率怎么表示 ? (3) 设哪个未知数 ? 相关的量怎样用它表示 ? (4) 根据怎样的数量关系列方程 ? 大亏本 大放血 5 折酬宾 清仓处理 跳楼价 销售和利率问题 知识探究 我思 , 故我进步 1 、商品原价 200 元，九折出售，卖价是 元 . 2 、商品进价是 30 元，售价是 50 元，则利润 是 元 . 2 、某商品原来每件零售价是 a 元 , 现在每件降价 10%, 降价后每件零售价是 　　　 元 . 3 、某种品牌的彩电降价 20% 以后，每台售价为 a 元，则该品牌彩电每台原价应为 　 　 元 . 4 、某商品按定价的八折出售，售价是 14.8 元，则原定售价是 　　　　 . 　　　　　　　　 0.9a 1.25a 18.5 元 180 20 思考？ 对上面商品销售中的问题里有哪些量 ? 成本价 ( 进价 ), 标价 ; 销售价 ; 利润 ; 盈利 ; 亏损 : 利润率 对上面这些量有何关系 ? 大家想一想！ = 商品售价 — 商品进价 ● 售价、进价、利润的关系式： 商品 利润 ● 进价、利润、利润率的关系 ： 利润率 = 商品进价 商品利润 ×100% ● 标价、折扣数、商品售价关系 : 商品售价＝ 标价 × 折扣数 10 ● 商品售价、进价、利润率的关系： 商品进价 商品售价 = ×(1+ 利润率 ) 销 售 中 的 等 量 关 系 驶向胜利的彼岸 ● 售价 × 件数 = 总金额 探究 1 问题 & 情境 分析：售价 = 进价 + 利润 售价 =(1+ 利润率 ) × 进价 分析 ：① 设 盈利 25% 衣服的进价是 元，则商品利润是 元；依题意列方程 由此得 x = ② 设亏损 25% 衣服的进价是 元，则商品利润是 元；依题意列方程 由此得 y = 两件衣服的进价是 x+y= （元） 两件衣服的售价是 （元） 因为 进价 售价 所以可知卖这两件衣服总的盈亏情况是 . x 0.25x x + 0.25x = 60 48 y -0.25y y + （ -0.25y ） =60 80 48+80=128 60×2=120 > 亏损 解：设盈利 25% 的那件衣服的进价是 x 元 , 另一 件的进价为 y 元，依题意，得 x+0.25x=60 解得 x=48 y － 0.25y=60 解得 y=80 60+60 － 48 － 80= － 8( 元 ) 答：卖这两件衣服总的亏损了 8 元。 课内练习 （ 1 ）广州某琴行同时卖出两台钢琴，每台售价为 960 元。其中一台盈利 20% ，另一台亏损 20% 。这次琴行是盈利还是亏损，或是不盈不亏？ 解：设盈利 20% 的那台钢琴进价为 x 元，它的 利润是 0.2x 元，则 x+0.2x=960 得 x=800 设亏损 20% 的那台钢琴进价为 y 元，它的利润是 0.2y 元，则 y-0.2y=960 得 y=1200 所以两台钢琴进价为 2000 元，而售价 1920 元，进价大于售价，因此两台钢琴总的盈利情况为亏本 80 元。 （ 2 ） 某文具店有两个进价不同的计算器都卖 64 元，其中一个盈利 60% ，另一个亏本 20%. 这次交易中的盈亏情况？ 解：设盈利 60% 的那个计算器进价为 X 元，它的利润是 0.6X 元，则 X+0.6X=64 得 X=40 设亏本 20% 的那个计算器进价为 Y 元，它的利润是 0.2Y 元，则 Y – 0.2Y=64 得 Y=80 所以两个计算器进价为 120 元，而售价 128 元，进价小于售价，因此两个计算器总的盈利情况为盈利 8 元 . 请再做一做 : 探索新知： 问题 2 某商店为了促销 G 牌空调机，承诺 2004 年元旦那天购买该机可分两期付款，即在购买时先付一笔款，余下部分及它的利息（年利率为 5.6% ）在 2005 年元旦付清，该空调机售价为每台 8224 元 . 若两次付款数相同，那么每次应付款多少元？ 你会了吗？ 解：设每次付款为 x 元 , 依题意得 (8224-x)(1+5.6%)=x 解得 x=4224 答：每次付款 4224 元 . 做一做 1 、某商场把进价为 1980 元的商品按标价的八折出售，仍获利 10%, 则该商品的标价为 元 . 解：设该商品的标价为 x 元． 　 0.8x=1980(1+0.1) 解得　　 x=2722.5 答：设该商品的标价为 2722.5 元． 解 : 设在 2005 年涨价前的价格为 x 元 . （ 1+0.3 ）（ 1 － 0.7 ） x=a 解得　　 x= 2 、我国政府为解决老百姓看病难的问题，决定下调药品的价格，某种药品在 2005 年涨价 30% 后， 2007 降价 70% 至 a 元，则这种药品在 2005 年涨价前价格为 元 . 答： 在 2005 年涨价前的价格为　　元 . 拓展提高 某商场把进价为 800 元的商品按标价的八折出售，仍获利 10%, 则该商品的标价为多少元？ 解：设该商品的标价为 x 元． 进价 + 进价 × 利润率 = 标价 × 折扣数 10 800 800 10% x 80% 800+800×10%=80%x 解得　　 x=1100 答：设该商品的标价为 1100 元． 小结 : 通过本节课的学习你有哪些收获？你还有哪些疑惑？ 熟记下列关系式 = 商品售价 — 商品进价 ● 售价、进价、利润的关系式： 商品 利润 ● 进价、利润、利润率的关系 ： 利润率 = 商品进价 商品利润 ×100% ● 标价、折扣数、商品售价关系 : 商品售价＝ 标价 × 折扣数 10 ● 商品售价、进价、利润率的关系： 商品进价 商品售价 = ×(1+ 利润率 ) 1 、某商品的进价是 1000 元，售价是 1500 元，由于销售情况不好，商店决定降价出售，但又要保证利润率不低于 5%, 那么商店最多可降多少元出售此商品？ 大展身手 2 、一年定期的存款，年利率为 1.98%, 到期取款时须扣除利息的 20%, 作为利息税上缴国库，假如某人存入一年的定期储蓄 1000 元，到期扣税后可得利息多少元？ 3 、某商场将某种 DVD 产品按进价提高 35%, 然后打出 “ 九折酬宾，外送 50 元打的费 ” 的广告，结果每台 DVD 仍获利 208 元，则每台 DVD 的进价是多少元？ 4 、国家规定个人发表文章或出书获得稿费的纳税计算方法是：（ 1 ）稿费不高于 800 元的不纳税；（ 2 ）稿费高于 800 元又不高于 4000 元的应交超过 800 元那一部分稿费 14% 的税；（ 3 ）稿费高于 4000 元的应交全部稿费的 11% 的税。王老师曾获得一笔稿费，并交纳个人所得税 280 元，那么王老师的这笔稿费共多少元？ 思考题 自主探究发现 【 情景 】 一般情况下，个体服装店只要高出进价的 20﹪ （公平买卖）便可盈利，但经销商们常常以高出进价的 80﹪ ～ 100 ﹪ 标价，然后进行打折销售，或者与顾客讨价还价 . 一天，小明的妈妈从个体服装店买回一件成衣，花去 220 元，回家后高兴的对小明说：“今天我捡了个大便宜，碰上服装八折优惠酬宾 ，平时要花 275 元的衣服我只要花了 220 元就买回来了 .” 1. 试估算一下该衣服的进价？ 3. 小明的妈妈真的捡便宜了吗？若没有，请你帮她计算一下，她比在公平买卖时多付出多少元钱？（计算过程中保留一位小数 ). 本题给了我们什么启示？ 2. 如果该件衣服是商家在进价的基础上加价 80﹪ 标价，则多少钱买这件衣服才算公平买卖（加 20﹪ ）？ 行程问题 一元一次方程的应用 相遇、追及问题 行程问题 一、本课重点 1. 基本关系式： _________________ 2. 基本类型： 相遇问题 ; 相距问题 3. 基本分析方法：画示意图分析题意，分清速度及 时间，找等量关系（路程分成几部分） . 4. 航行问题的数量关系： （ 1 ）顺流（风）航行的路程 = 逆流（风）航行的路程 （ 2 ）顺水（风）速度 =_________________ 逆水（风）速度 =_________________ 路程 = 速度 X 时间 静水（无风）速 + 水（风）速 静水（无风）速 — 水（风）速 一、相遇问题的基本题型 1 、同时出发（两段） 二、相遇问题的等量关系 2 、不同时出发 （三段 ） 二、基础题 1 、甲的速度是每小时行 4 千米，则他 x 小时行（ ）千米 . 2 、乙 3 小时走了 x 千米，则他的速度（ ） . 3 、甲每小时行 4 千米，乙每小时行 5 千米，则甲、 乙 一小时共行（ ）千米， y 小时共行（ ）千米 . 4 、某一段路程 x 千米，如果火车以 49 千米 / 时的速度行驶，那么火车行完全程需要（ ）小时 . 4X X/3 9 9y X/49 若明明以每小时 4 千米的速度行驶上学，哥哥半小时后发现明明忘了作业，，就骑车以每小时 8 千米追赶，问哥哥需要多长时间才可以送到作业？ 解：设哥哥要 X 小时才可以送到作业 8X = 4X + 4×0.5 解得 X = 0.5 答：哥哥要 0.5 小时才可以把作业送到 家 学 校 追 及 地 4×0.5 4X 8X 敌军在早晨 5 时从距离我军 7 千米的驻地开始逃跑，我军发现后立即追击，速度是敌军的 1.5 倍，结果在 7 时 30 分追上，我军追击速度是多少？ 智力冲浪 7 千米 2.5X 2.5(1.5X) 三、综合题 1. 甲、乙两地路程为 180 千米，一人骑自行车从甲地出发每时走 15 千米，另一人骑摩托车从乙地出发，已知摩托车速度是自行车速度的 3 倍，若两人同时出发，相向而行，问经过多少时间两人相遇？ 2. 甲、乙两地路程为 180 千米，一人骑自行车从甲地出发每时走 15 千米，另一人骑摩托车从乙地出发，已知摩托车速度是自行车速度的 3 倍，若两人同向而行，骑自行车在先且先出发 2 小时， 问摩托车经过多少时间追上自行车？ 3 ．一架直升机在 A ， B 两个城市之间飞行，顺风飞行需要 4 小时，逆风飞行需要 5 小时 . 如果已知风速为 30km/h ，求 A ， B 两个城市之间的距离 . 4. 甲、乙两人都以不变速度在 400 米的环形跑道上跑步，两人在同一地方同时出发同向而行，甲的速度为 100 米 / 分乙的速度是甲速度的 3/2 倍，问（ 1 ）经过多少时间后两人首次遇（ 2 ）第二次相遇呢？ 相等关系： A 车路程 ＋ B 车路程 = 相距路程 相等关系： 总量 = 各分量之和 想一想回答下面的问题： 1 、 A 、 B 两车分别从相距 S 千米的甲、乙两地同时出发， 相向 而行，两车会相遇吗？ 导入 　 甲 乙 A B 2 、如果两车相遇，则相遇时两车所走的路程与 A 、 B 两地的距离有什么关系？ 相遇问题 想一想回答下面的问题： 3 、如果两车同向而行， B 车先出发 a 小时，在什么情况下两车能相遇？为什么？ A 车速度 〉 乙车速度 4 、如果 A 车能追上 B 车，你能画出线段图吗？ 甲 乙 A （ B ） 相等关系： B 车先行路程 ＋ B 车后行路程 =A 车路程 例 1 、 A 、 B 两车分别停靠在相距 240 千米的甲、乙两地，甲车每小时行 50 千米，乙车每小时行 30 千米。 （ 1 ）若两车同时 相向 而行，请问 B 车行了多长时间后与 A 车相遇？ 精讲 例题 分 析 甲 乙 A B A 车路程＋ B 车路程 = 相距路程 线段图分析： 若设 B 车行了 x 小时后与 A 车相遇，显然 A 车相遇时也行了 x 小时。则 A 车路程为 千米； B 车路程 为 千米。根据相等关系可列出方程。 相等关系： 总量 = 各分量之和 例 1 、 A 、 B 两车分别停靠在相距 240 千米的甲、乙两地，甲车每小时行 50 千米，乙车每小时行 30 千米。 （ 1 ）若两车同时 相向 而行，请问 B 车行了多长时间后与 A 车相遇？ 精讲 例题 分 析 甲 乙 A B A 车路程＋ B 车路程 = 相距路程 解：设 B 车行了 x 小时后与 A 车相遇，根据题意列方程得 50x+30x=240 解得 x=3 答： 设 B 车行了 3 小时后与 A 车相遇。 例 1 、 A 、 B 两车分别停靠在相距 240 千米的甲、乙两地，甲车每小时行 50 千米，乙车每小时行 30 千米。 （ 2 ）若两车同时相向而行，请问 B 车行了多长时间后两车相距 80 千米？ 精讲 例题 分 析 线段图分析： 甲 乙 A B 80 千米 第一种情况： A 车路程＋ B 车路程＋相距 80 千米 = 相距路程 相等关系： 总量 = 各分量之和 例 1 、 A 、 B 两车分别停靠在相距 240 千米的甲、乙两地，甲车每小时行 50 千米，乙车每小时行 30 千米。 （ 2 ）若两车同时相向而行，请问 B 车行了多长时间后两车相距 80 千米？ 精讲 例题 分 析 线段图分析： 甲 乙 A B 80 千米 第二种情况： A 车路程＋ B 车路程 - 相距 80 千米 = 相距路程 1 、 A 、 B 两车分别停靠在相距 115 千米的甲、乙两地， A 车每小时行 50 千米， B 车每小时行 30 千米， A 车出发 1.5 小时后 B 车再出发。 （ 1 ）若两车相向而行，请问 B 车行了多长时间后与 A 车相遇？ 变式 练习 分 析 相等关系： A 车路程＋ A 车同走的路程 + B 车同走的路程 = 相距路程 线段图分析： 甲 乙 A B 1 、 A 、 B 两车分别停靠在相距 115 千米的甲、乙两地， A 车每小时行 50 千米， B 车每小时行 30 千米， A 车出发 1.5 小时后 B 车再出发。 （ 2 ）若两车相向而行，请问 B 车行了多长时间后两车相距 10 千米？ 变式 练习 分 析 线段图分析： 甲 乙 A B 甲 乙 A B 家 学 校 追 及 地 400 米 80x 米 180x 米 例 2 、小明每天早上要在 7:50 之前赶到距离家 1000 米的学校上学，一天，小明以 80 米 / 分的速度出发， 5 分后，小明的爸爸发现他忘了带语文书，于是，爸爸立即以 180 米 / 分的速度去追小明，并且在途中追上他。 （ 1 ）爸爸追上小明用了多少时间？ （ 2 ）追上小明时，距离学校还有多远？ 精讲 例题 分 析 相等关系： 小明先行路程 ＋ 小明后行路程 = 爸爸的路程 家 学 校 追 及 地 400 米 80x 米 180x 米 例 2 、小明每天早上要在 7:50 之前赶到距离家 1000 米的学校上学，一天，小明以 80 米 / 分的速度出发， 5 分后，小明的爸爸发现他忘了带语文书，于是，爸爸立即以 180 米 / 分的速度去追小明，并且在途中追上他。 （ 1 ）爸爸追上小明用了多少时间？ （ 2 ）追上小明时，距离学校还有多远？ 精讲 例题 分 析 （ 1 ）解：设爸爸要 x 分钟才追上小明，依题意得： 180x = 80x + 5×80 解得 x=4 答：爸爸追上小明用了 4 分钟。 2 、 A 、 B 两车分别停靠在相距 115 千米的甲、乙两地， A 车每小时行 50 千米， B 车每小时行 30 千米， A 车出发 1.5 小时后 B 车再出发。 若两车 同向而行 （ B 车在 A 车前面），请问 B 车行了多长时间后被 A 车追上？ 变式 练习 分 析 线段图分析： 甲 A B 50 × 1.5 50x 30x 乙 115 相等关系： A 车先行路程 + A 车后行路程 - B 车路程 = 115 3 、小王、叔叔在 400 米长的环形跑道上练习跑步，小王每秒跑 5 米，叔叔每秒跑 7.5 米。 （ 1 ）若两人同时同地 反向 出发，多长时间两人首次相遇？ （ 2 ）若两人同时同地 同向 出发，多长时间两人首次相遇？ 变式 练习 分 析 （ 1 ）反向 相等关系： 小王路程 + 叔叔路程 = 400 叔叔 小王 3 、小王、叔叔在 400 米长的环形跑道上练习跑步，小王每秒跑 4 米，叔叔每秒跑 7.5 米。 （ 1 ）若两人同时同地 反向 出发，多长时间两人首次相遇？ （ 2 ）若两人同时同地 同向 出发，多长时间两人首次相遇？ 变式 练习 分 析 （ 2 ）同向 相等关系： 小王路程 + 400 = 叔叔路程 叔叔 小王 归纳： 在列一元一次方程解行程问题时 , 我们常画出线段图来分析数量关系。用线段图来分析数量关系能够帮助我们更好的理解题意，找到适合题意的等量关系式，设出适合的未知数 , 列出方程。正确地作出线段图分析数量关系，能使我们分析问题和解问题的能力得到提高。 用一元一次方程分析和解决实际问题的基本过程如下 : 实际问题 数学问题 ( 一元一次方程 ) 实际问题的答案 数学问题的解 (x=a) 列方程 检验 解方程 小结： 这节课我们复习了 行程问题中的相遇和追及问题 ，归纳如下： 相遇 A 车路程 B 车路程 相等关系： A 车路程 +B 车路程 = 相距路程 A 车后行路程 B 车追击路程 A 车先行路程 追击 相等关系： B 车路程 =A 车先路程 +A 车后行路程 或 B 车路程 =A 车路程 + 相距路程 数字问题 一元一次方程的应用 预备知识： 1 、多位数的表示方法： ① 若一个两位数的个位上的数字为 a ，十位上的数字为 b ，则这个两位数是 _______ ； ② 若一个三位数的个位上的数字为 a ，十位上的数字为 b ，百位上的数字为 c ，则这个三位数是 ________________ ； ③ 四、五 … 位数依此类推。 10b+a 100c+10b+a 2 、连续数的表示方法： ① 三个连续整数为： n-1 ， n ， n+1 （ n 为整数） ② 三个连续偶数为： n-2 ， n ， n+2 （ n 为偶数） 或 2n-2 ， 2n ， 2n+2 （ n 为整数） ③ 三个连续奇数为： n-2 ， n ， n+2 （ n 为奇数） 或 2n-1 ， 2n+1 ， 2n+3 （ n 为整数） 3 、日历上的数字：在日历中用长方形框 9 个数字，设正中间的数为 a ，则其它数如下表： a-8 a-7 a-6 a-1 a a+1 a+6 a+7 a+8 例 1 、三个连续偶数之和比最大一个偶数的 2 倍数多 12 ，求这三个数。 解：设三个连续偶数的中间一个数是 x ， 则另两个数分别是 x-2,x+2. 依题意得 x+x-2+x+2=2(x+2)+12 解得 x=16 所以 当 x=16 时， x-2=14; x+2=18; 答：这三个连续偶数分别是 14 、 16 和 18 。 例 2 、某两位数，数字之和为 8 ，将这个两位数的数字位置对换，得到的新两位数比原两位数小 18 ，求原来的两位数。 解：设这个两位数个位上的数字是 x ，则十位上的数字是 8-x ，那么这个两位数是 10(8-x)+x ；这个两位数的数字位置对换，得到的新两位是 10x+(8-x). 依题意得 10x+(8-x)=10(8-x)+x-18 解得 x=3 答：原来的两位数是 53 。 例 3 、用正方形圈出日历中的 4 个的和是 76 ，这 4 天分别是几号？ x x+1 x+7 x+8 解：设用正方形圈出的 4 个日子如下表： 依题意得 x+x+1+x+7+x+8=76 解得 x=15 所以 当 x=15 时， x+1=16; x+7=22; x+8=23; 答：这 4 天分别是 15 、 16 、 22 、 23 号。 ② 如果设第一个数为 x ，则其它两个数可表示为 x+7 ， x+14 ； ③ 如果设第三个数为 x ，则其它两个数可表示为 x-14 ， x-7 。 如果设其中的一个数为 x ，那么其他两个数怎样表示？你是怎样设未知数的？ 答： ①如果设中间的数为 x ，则 其它两个数可表示为 x-7 ， x+7 ； ② 若设第一个数为 x ，则有 x+x+7+x+14=60 ③ 若设第三个数为 x ，则有 x-14+x-7+x=60 观察一下，哪种设法解方程时最简单？ ① 若设中间的数为 x ，则有 x-7+x+x+7=60 根据游戏中的问题，用你所设的未知数 x ，列出方程，求出这三天分别是几号。 因此，这三天分别是 13 号， 20 号， 27 号。 当 x=20 时， x-7=13 ， x+7=27 x-7+x+x+7=60 解得 x=20 解：设中间的数为 x ，则其它两个数分别为 x-7 ， x+7 ；根据题意，得 当 x=25 时， x-7=18 ， x+7=32 如果小颖说的出是 75 ，你认为可能吗？为什么？ 解：设中间的数为 x ，则其它两个数分别为 x-7 ， x+7 ；根据题意，得 x-7+x+x+7=75 解得 x=25 质疑：在一年中任何一个月中有没有 32 号这一天？ 所以小颖说的出是 75 ，是不可能的。 解：设中间的数为 x ，则其它两个数分别为 x-7 ， x+7 ；根据题意，得 x-7+x+x+7=21 3x=21 x=7 当 x=7 时， x-7=0 ， x+7=14 因为在一年中任何一个月中都没有 0 号这一天，所以这种情况不会出现。 如果小颖说的出是 21, 你认为可能吗？为什么 ? 两人一组 做下面的游戏 ： （ 1 ）每人准备一份日历，在各自的日历上任意圈出一个数列上相邻的 4 个数。两人分别把自己所圈中的 4 个数的和告诉同伴，由同伴求出这 4 个数分别是多少？ 做一做 （ 2 ）在各自的日历上，用一个正方形任意圈出 2×2 个数，把它们的和告诉同伴，由同伴求出这 4 个数分别是多少？ 小组合作探究 下面三个方框，每个方框共有九个日期，任意填出一个日期数，你能根据日历中各数的排列规律猜出另外的几个日期数吗？请说明理由。 5 9 12 观察上面的三个方框你还能得出什么规律？ 练习： 1 、三个连续奇数的和为 69 ，则这三个数是 。 2 、一个两位数，个位上的数是十位上的数的 2 倍，如果把十位与个位上的数对调，那么所得到的两位数比原两位大 36 ，则原两位数是 。 3 、你假期外出旅行一周，这一周各天的日期之和是 84 ，那么旅行社是 _____ 号送你回家的 . 4 、日历中同一竖列相邻三个数的和可以是（ ） A 、 78 B 、 26 C 、 21 D 、 45 ； 21 、 23 、 25 48 15 D 5 、 你能在日历中圈出一个竖列上相邻的 3 个数，使得它们的和是 40 吗？为什么？ 答：不能，可以从下面两个方面来分析原因： （ 1 ）如果设中间那个数为 x ，根据题意，得 (x-7)+x+(x+7)=40 解得： x= ，不符合实际； （ 2 ）通过观察与研究，可知日历中一竖列上相邻的 3 个数的和一定是三的倍数，而 40 不是，故不能。 图表问题 一元一次方程的应用 0 22 22 通过观察积分表，你能得到哪些信息? 球赛积分表问题 18 4 40 18 4 40 14 8 36 14 8 36 12 10 34 12 10 34 11 11 33 10 12 32 10 12 32 7 15 29 6 16 28 2000 赛季全国男篮甲 A 联赛常规赛最终积分榜 0 22 22 负一场积1分 2000 赛季全国男篮甲 A 联赛常规赛最终积分榜 设胜一场积ｘ分， 你能求出胜一场积几分吗？ 例如：从第一行得方程 胜一场积 2 分 试一试： ｘ＝２ １８ｘ＋１ × ４＝４０ 从表中其他任何一行可以列方程，求出ｘ的值 18 4 40 14 8 36 12 10 34 11 11 33 10 12 32 7 15 29 6 16 28 18 4 40 14 8 36 12 10 34 10 12 32 0 22 22 负场积分为 _________, 列式表示积分与胜、负场数之间的数量关系 结论： 负一场积 1 分 胜一场积 2 分 则胜场积分为 _____, 解 : 如果一个队胜 m 场，则负 __________ 场， （ 22 － m ） 2m 22 － m 2m ＋（ 22 － m ）＝ m ＋ 22 总积分为 18 4 40 14 8 36 12 10 34 11 11 33 10 12 32 7 15 29 6 16 28 18 4 40 14 8 36 12 10 34 10 12 32 0 22 22 试一试： 2000 赛季全国男篮甲 A 联赛常规赛最终积分榜 队名 比赛场次 胜场 负场 积分 八一双鹿 22 18 4 40 上海东方 22 18 4 40 北京首钢 22 14 8 36 吉林恒和 22 14 8 36 辽宁盼盼 22 12 10 34 广东宏运 22 12 10 34 前卫奥神 22 江苏南钢 22 10 12 32 山东润洁 22 10 12 32 浙江万马 22 7 15 29 双星济军 22 6 16 28 沈部雄狮 22 0 22 22 负场比胜场的2倍少11场 想一想： 2000 赛季全国男篮甲 A 联赛常规赛最终积分榜 队名 比赛场次 胜场 负场 积分 八一双鹿 22 18 4 40 上海东方 22 18 4 40 北京首钢 22 14 8 36 吉林恒和 22 14 8 36 辽宁盼盼 22 12 10 34 广东宏运 22 12 10 34 前卫奥神 22 江苏南钢 22 10 12 32 山东润洁 22 10 12 32 浙江万马 22 7 15 29 双星济军 22 6 16 28 沈部雄狮 22 0 22 22 11 11 33 X 表示所胜的场数，必须是整数，所以 不符合实际。 X= 注意： 解决实际问题时，要考虑得到的结果是不是符合实际。 由此可以判定没有哪个队的胜场总积分等于负场总积分。 有没有某队的胜场总积分能等于负场总积分吗？ 猜一猜 X 表示什么量 ? 它可以是分数吗 ? 想一想 18 4 40 14 8 36 12 10 34 11 11 33 10 12 32 7 15 29 6 16 28 18 4 40 14 8 36 12 10 34 10 12 32 0 22 22 2 、用方程解决实际问题时，不仅要注意解方程的过程是否正确，还要检验方程的解是否符合问题的 实际意义 。 1 、利用方程不仅能求未知数值，而且可以进行 推理判断 。 通过例题学习，你有什么体会？ 议一议： 暑假里,《新晚报》组织了我们的小世界杯足球邀请赛，勇士队在第一轮比赛中共 赛了9场,得分17分 。比赛规定 胜一场得3分,平一场得1分,负一场得0分 , 勇士队在这一轮比赛中只 负了2场 ,那么这个队胜了几场?又平了几场呢? 试一试 练一练 在一次有12支球队参加的足球循环赛中（每两队必须赛一场），规定胜一场3分，平一场1分，负一场0分，某队在这次循环赛中所胜场数比所负的场数多两场，结果得18分，那么该队胜了几场？ 试一试 练一练 如图是一张有 4 人参加的某项棋类循环比赛额定积分表，每场比赛胜者得 3 分，负者得－ 1 分，和局两人各得 1 分。 （ 1 ）填出表内空格的分值； （ 2 ）排除这次比赛的名次。 甲 乙 丙 丁 总分 甲 3 1 乙 －1 丙 1 3 丁 3 － 1 － 1 1 5 1 3 － 3 3 7 ∴ 第一名： － 1 丁 第二名： 甲 第三名： 丙 第四名： 乙 挑战自我 下表中记录了一次试验中时间和温度的数据 时间/分 0 5 10 15 20 25 温度/℃ 10 25 40 55 70 85 （1）如果温度的变化是均匀的，21分的温度是多少？ （2）什么时间的温度是34 ℃？ 挑战自我 一次足球赛11轮(即每队均需赛11场),胜一场记2分,平一场记1分,负一场记0分,北京国安队所负场数是所胜场数的 ,结果共得14分,求国安队共平了多少场? 拓展思维 六 .『 调配问题 』 例： 在甲处劳动的有 27 人，在乙处劳动的有 19 人，现在另调 20 人去支援，使在甲处的人数为在乙处的人数的 2 倍，应调往甲、乙两处各多少人？ 调配问题 一元一次方程的应用 为鼓励节约用水，某地按以下规定收取每月的水费：如果每月每户用水不超过 20 吨，那么每吨水按 1.2 元收费；如果每月每户用水超过 20 吨，那么超过的部分按每吨 2 元收费。若某用户五月份的水费为平均每吨 1.5 元，问，该用户五月份应交水费多少元？ 3 、 甲仓库储粮 35 吨 ，乙仓库储粮 19 吨，现调粮食 15 吨，应分配给两 仓库各多少吨，才能使得甲仓库的粮食数量是乙仓库的两倍？ 分析 ： 若设应分给甲仓库粮食 X 吨，则数量关系如下表 原有粮食 新分给粮食 现有粮食 甲仓库 35 X 35+X 乙仓库 19 (15 － X) 19+(15 － X) 故相等关系为 ： 甲仓库现有粮食的重量＝ 2× 乙仓库现有粮食的重量 解 ： 设应分给甲仓库粮食 X 吨，则应分给乙仓库粮食（ 15 － X) 吨。 依题意得 解之得 X ＝ 11 则 15 － X ＝ 4 答 ： 应分给甲仓库 11 吨粮食，分给乙仓库 4 吨粮食。 例　学校组织植树活动，已知在甲处植树的有 23 人，在乙处植树的有 17 人，现调 20 人去支援，使在甲处植树的人数是乙处植树人数的 2 倍，应调往甲、乙两处各多少人？ 分析： 23 17 x 20 － x 23+x 17+20 － x 等量关系： 甲处增加后人数 = 乙处增加后人数的 2 倍 例 2 小明想在两种灯中选购一种 , 其中一种是 11 瓦 ( 即 0.011 千瓦 ) 的节能灯 , 售价 60 元 ; 另一种是 60 瓦 ( 即 0.06 千瓦 ) 的白炽灯 , 售价 3 元 . 两种灯的照明效果一样 , 使用寿命也相同 (3000 小时以上 ). 节能灯售价较高 , 但是较省电 ; 白炽灯售价低 , 但是用电多 . 如果电费是 0.5 元 /( 千瓦时 ), 选哪种灯可以节省电费 ( 灯的售价加电费 )? 分析 : 问题中有基本等量关系 : 费用 = 灯的售价 ＋ 电费 ; 电费 =0.5 × 灯的功率 ( 千瓦 ) × 照明时间 ( 时 ). (1) 设照明时间为 t 小时 , 则 总费用 售价 电费 节能灯 60 元 白炽灯 3 元 (2) 用特殊值试探 : 节能灯的总费用为 : 60 ＋ 0.5×0.011t =60 ＋ 0.5×0.011 × 2000=71 ; 白炽灯的总费用为 : 3 ＋ 0.5×0.06t =3 ＋ 0.5×0.06 × 2000=63; 如果取 t=2000 时 , 60 ＋ 0.5×0.011t 3 ＋ 0.5×0.06t 0.5×0.011t 0.5×0.06t 由两组数值可以说明 , 照明时间不同 , 为了省钱而选择用哪种灯的答案也不同 . 如果取 t=2500 呢 ? 请你算一算节能灯与白炽灯哪个费用较低 ? 解 : 设照明时间为 t 小时 , 则节能灯的总费用为 [ 60 ＋ 0.5×0.011t ] 元 ; 白炽灯的总费用为 [ 3 ＋ 0.5×0.06t ] 元 ; 如果两个总费用相等 , 则有 60 ＋ 0.5×0.011t =3 ＋ 0.5×0.06t 解此方程得 :t≈2327( 小时 ) 因此我们可以取 t=2000 小时和 t=2500 小时 , 分别计算节能灯和白炽灯的总费用 当 t=2000 时 , 节能灯的总费用为 : 60 ＋ 0.5×0.011t =60 ＋ 0.5×0.011 × 2000=71; 白炽灯的总费用为 : 3 ＋ 0.5×0.06t =3 ＋ 0.5×0.06 × 2000=63 ; 因此由方程的解和试算判断 : 在 t<2327 小时时 , 选择白炽灯优惠一些 ; 在 t=2327 小时时 , 两种等的总费用一样 ; 在 t>2327 小时而不超过使用寿命时 , 选择节能灯优惠一些 . 当 t=2500 时 , 节能灯的总费用为 : 60 ＋ 0.5×0.011 × 2500=73.75; 白炽灯的总费用为 : 3 ＋ 0.5×0.06 × 2500=78 ; 例 2 小明想在两种灯中选购一种 , 其中一种是 11 瓦 ( 即 0.011 千瓦 ) 的节能灯 , 售价 60 元 ; 另一种是 60 瓦 ( 即 0.06 千瓦 ) 的白炽灯 , 售价 3 元 . 两种灯的照明效果一样 , 使用寿命也相同 (3000 小时以上 ). 节能灯售价较高 , 但是较省电 ; 白炽灯售价低 , 但是用电多 . 如果电费是 0.5 元 /( 千瓦时 ), 选哪种灯可以节省电费 ( 灯的售价加电费 )? 问题 : 如果灯的使用寿命都是 3000 小时 , 而计划照明 3500 小时 , 则需要购买两个灯 , 试设计你认为能省钱的选灯方案 . 参考方案 : 买白炽灯和节能灯各一只 , 用白炽灯照明 500 小时 , 节能灯照明 3000 小时 . 在这种方案中的总费用为 : 60 ＋ 0.5×0.011×3000 ＋ 3 ＋ 0.5×0.06×500 =60 ＋ 16.5 ＋ 3 ＋ 15 =94.5( 元 ) 你的方案的总费用是多少 ?