- 431.50 KB
- 2021-04-17 发布
四川省泸县五中2019-2020学年高二上学期期末模拟考试理科数学试题
第I卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每个小题所给出的四个选项中,只 有一项是符合题目要求的,把正确选项的代号填在答题卡的指定位置.)
1.某鱼贩一次贩运草鱼、青鱼、鲢鱼、鲤鱼及鲫鱼分别有80条、20条、40条、40条、20条,现从中抽取一个容量为20的样本进行质量检测,若采用分层抽样的方法抽取样本,则抽取的青鱼与鲤鱼共有
A.6条 B.8条 C.10条 D.12条
2.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员按成绩由好到差编为1﹣35号,再用系数抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是
A. 3 B. 4 C. 5 D. 6
3.若变量 , 满足约束条件 ,则 的最小值为
A.-7 B.-1 C.1 D.2
4.某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为
A. 63.6万元 B. 65.5万元 C. 67.7万元 D. 72.0万元
5.点 到直线 的距离是
A. B. C.1 D.
6.如图所示,程序的输出结果为S=132,则判断框中应填
A.i≥10? B.i≥11? C.i≤11? D.i≥12?
7.已知命题;命题若,则.则下列命题为真命题的是
A. B. C. D.
8.若直线 : 与直线 : 平行,则 的值为
A. B. C. D.
9.若,且,则
A. B. C. D.
10.若圆 与圆 相切,则 等于
A.16 B.7 C.-4或16 D.7或16
11.已知圆 ,圆 , 分别是圆 和圆 上的动点,点 是 轴上的动点,则 的最大值为
A. B. C. D.
12.已知 为坐标原点,设 , 分别是双曲线 的左、右焦点,点 为双曲线左支上任一点,过点 作 的平分线的垂线,垂足为 ,若 ,则双曲线的离心率是
A. B. C. D.
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,满分20分)
13.命题,使得,则是__________.
14.关于不等式的解集为 ,则_____________
15.《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵.斜解壍堵,其一为阳马,一为鳖臑.”这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥.已知三棱锥 是一个“鳖臑”, 平面 , ,且 , ,则三棱锥 的外接球的表面积为 .
16.为抛物线上一点,过点作垂直该抛物线的准线于点为抛物线的焦点,为坐标原点,若四边形的四个顶点在同一个圆上,则该圆的面积为_______.
三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤)
17.(10分)
已知p:,,q:,,
(Ⅰ)若q是真命题,求m的范围;
(Ⅱ)若为真,求实数m的取值范围
18.(12分)
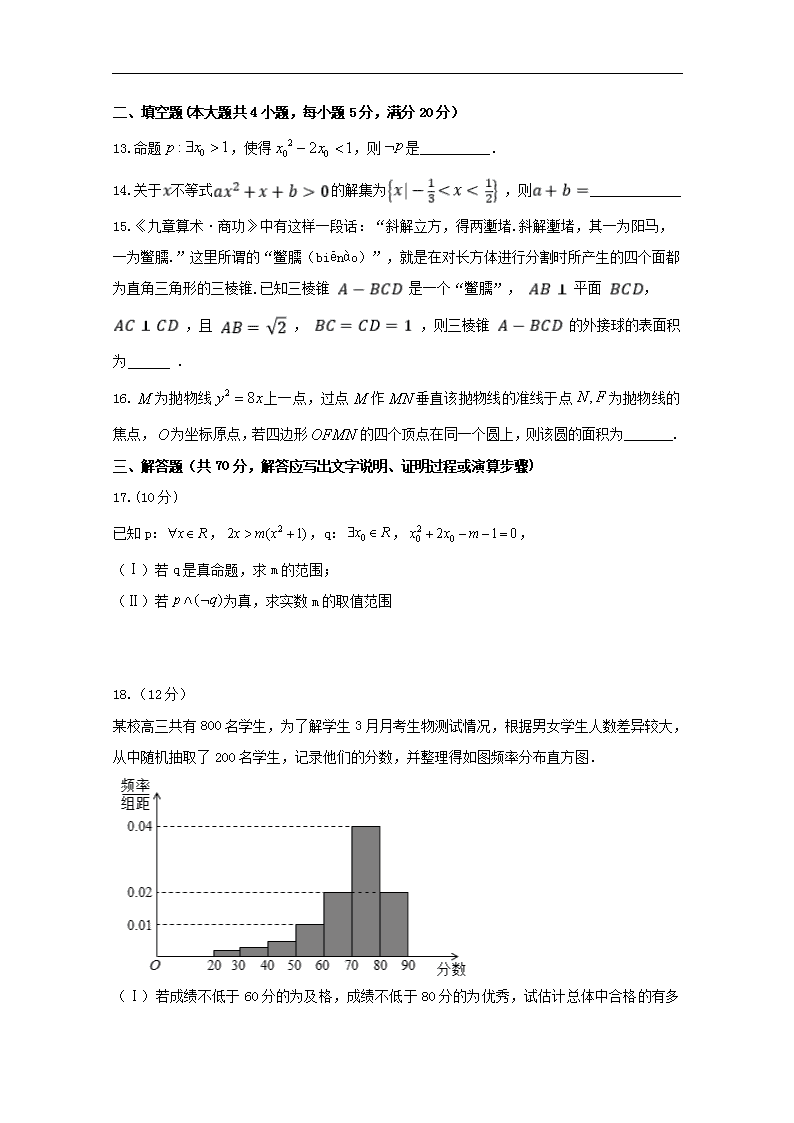
某校高三共有800名学生,为了解学生3月月考生物测试情况,根据男女学生人数差异较大,从中随机抽取了200名学生,记录他们的分数,并整理得如图频率分布直方图.
(Ⅰ)
若成绩不低于60分的为及格,成绩不低于80分的为优秀,试估计总体中合格的有多少人?优秀的有多少人?
(Ⅱ)已知样本中有一半的女生分数不小于80,且样本中不低于80分的男女生人数之比2:3,试估计总体中男生和女生人数的比例.
19.(12分)
已知圆 的圆心在直线 上,且圆 经过点 .
(Ⅰ)求圆的标准方程;
(Ⅱ)直线 过点 且与圆 相交,所得弦长为4,求直线 的方程.
20.(12分)
已知平面内一动点 到点 的距离与点 到 x 轴的距离的差等于1.
(Ⅰ)求动点 的轨迹 的方程;
(Ⅱ)过点 作两条斜率存在且互相垂直的直线 ,设 与轨迹 相交于点 , 与轨迹 相交于点 ,求 的最小值.
21.(12分)
如图,在三棱柱 中,侧棱 底面 ,且 , 是棱 的中点,点 在侧棱 上运动.
(Ⅰ)当 是棱 的中点时,求证: 平面 ;
(Ⅱ)当直线 与平面 所成的角的正切值为 时,求二面角 的余弦值.
22.设椭圆 ( )的右焦点为F,右顶点为A,已知 ,其中O 为原点, e为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点A的直线l与椭圆交于点B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H,若 ,且 ,求直线的l斜率.
2019年秋四川省泸县第五中学高二期末模拟考试
理科数学试题答案
1.A 2.B 3.A 4.B 5.A 6.B 7.B 8.D 9.A 10.C 11.A 12.D
13. 14.-5 15. 16.
17.(1) 若q:∃x0∈R,+2x0-m-1=0为真,则方程x2+2x-m-1=0有实根,
∴4+4(m+1)≥0,∴m≥-2.
(2)2x>m(x2+1)可化为mx2-2x+m<0.
若p:∀x∈R, 2x>m(x2+1)为真.
则mx2-2x+m<0对任意的x∈R恒成立.
当m=0时,不等式可化为-2x<0,显然不恒成立;
当m≠0时,有∴m<-1.
:m<-2
又为真,故p、Øq均为真命题.∴m<-2.
18.(1)根据频率分布直方图可知,
总体中及格的人数估计为,
总体中优秀的人数估计为,
所以估计总体中及格的有640人,优秀的有160人.
(2)由题意可知,样本中分数不小于80的学生人数为,
所以样本中分数不小于80的女生人数为,
所以样本中的女生人数为,男生人数为,
男生和女生人数的比例为,
所以根据分层抽样原理,总体中男生和女生人数的比例估计为.
19.(1)解:设圆心为 ,则 应在 的中垂线上,其方程为 ,
由 ,即圆心 坐标为
又半径 ,故圆的方程为
(2)解:点 在圆内,且弦长为 ,故应有两条直线.
圆心到直线距离 .
①当直线的斜率不存在时,直线的方程为 ,
此时圆心到直线距离为1,符合题意.
②当直线的斜率存在时,设为 ,直线方程为
整理为 ,则圆心到直线距离为
解得 ,直线方程为
综上①②,所求直线方程为 或
20. (1)解:设动点 的坐标为 ,由题意得
化简得 当 时 ;当 时x=0
所以动点P的轨迹 的方程为 和X=0( )
(2)解:由题意知,直线 的斜率存在且不为0,设为 ,则 的方程为 .
由
设 则
,
因为 ,所以 的斜率为 .设 ,则同理可得 ,
当且仅当 即 时, 取最小值16
21.(1)解:取线段 的中点 ,连结 .
∵ ,∴ ,且 .
又 为 的中点,∴ ,且 .
∴ ,且 .∴四边形 是平行四边形.∴ .
又 平面 平面 ,∴ 平面 .
(2)解:∵ 两两垂直,∴以 为原点, 所在直线分别为 轴, 轴, 轴,建立空间直角坐标系 ,如图,
∵三棱柱 中, 平面 ,∴ 即为直线 与平面 所成的角.
设 ,则由 ,得 .
∴ .∴
,
设平面 的一个法向量为 ,
则
令 ,得 ,即 .又平面 的一个法向量为 ,∴ ,
又二面角 的平面角为钝角,∴二面角 的余弦值为 .
22.解:(I)设 ,由 ,即 ,可得 ,又 ,所以 ,因此 ,所以椭圆的方程为 .
(Ⅱ)设直线的斜率为 ,则直线l的方程为 ,设 ,由方程组 消去y,整理得 ,
解得x=2或 ,
由题意得 ,从而 ,
由(1)知 ,设 ,有 , ,
由 ,得 ,所以 ,
解得 ,因此直线MH的方程为 ,
设 ,由方程组 消去y,得 ,
在 中, ,
即 ,化简得 ,即
,
解得 或 ,
所以直线l的斜率为 或