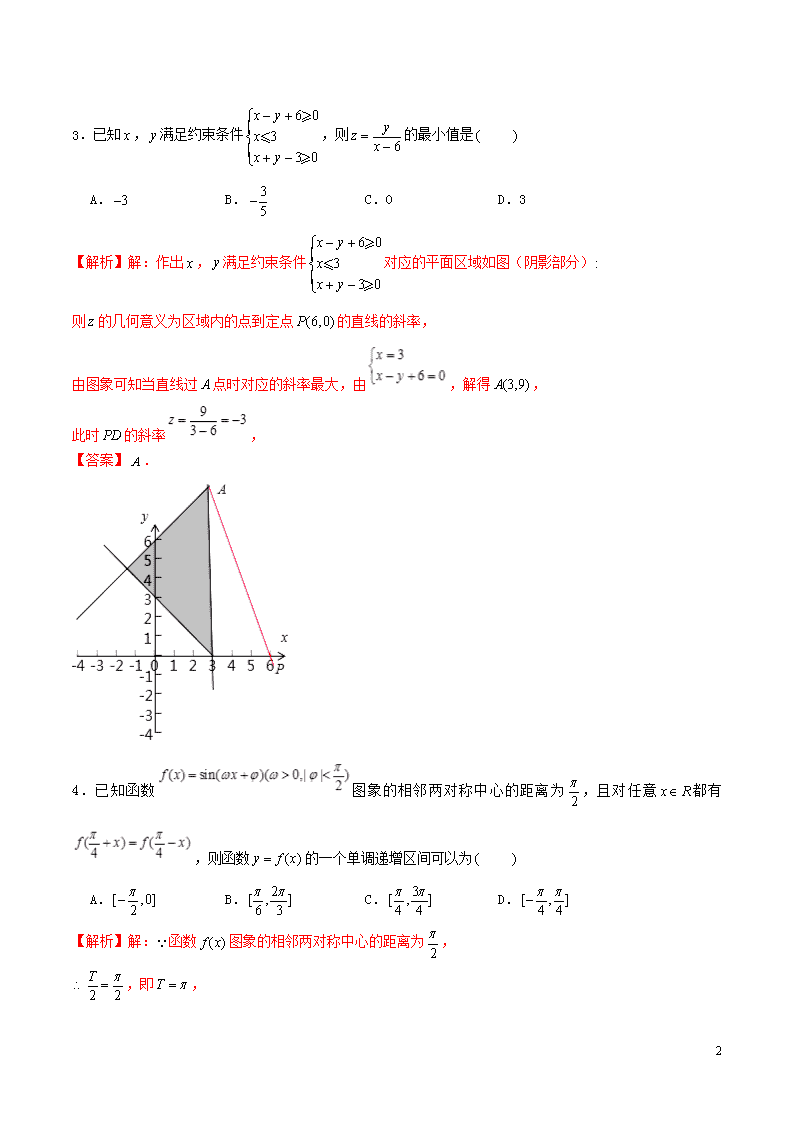2019年高考数学仿真押题试卷（十八）（含解析） 19页

专题18 高考数学仿真押题试卷（十八）‎ 注意事项：‎ ‎1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。‎ ‎2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎4．考试结束后，请将本试题卷和答题卡一并上交。‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，集合，则　　‎ A．， B． C．，， D．，，‎ ‎【解析】解：集合或，‎ 集合，‎ 或，，．‎ ‎【答案】． 2．已知为虚数单位，实数，满足，则的值为　　‎ A．6 B． C．5 D．‎ ‎【解析】解：，‎ ‎，解得．‎ 的值为6．‎ ‎【答案】． ‎ 19‎ ‎3．已知，满足约束条件，则的最小值是　　‎ A． B． C．0 D．3‎ ‎【解析】解：作出，满足约束条件对应的平面区域如图（阴影部分）‎ 则的几何意义为区域内的点到定点的直线的斜率，‎ 由图象可知当直线过点时对应的斜率最大，由，解得，‎ 此时的斜率，‎ ‎【答案】．‎ ‎ 4．已知函数图象的相邻两对称中心的距离为，且对任意都有，则函数的一个单调递增区间可以为　　‎ A． B． C． D．‎ ‎【解析】解：函数图象的相邻两对称中心的距离为，‎ ‎，即，‎ 19‎ ‎，，‎ 对任意都有，‎ 函数关于对称，‎ 即，，‎ 即，，‎ ‎，当时，，‎ 即，‎ 由，‎ 得，，‎ 即函数的单调递增区间为为，，，‎ 当时，单调递增区间为，，‎ ‎【答案】． 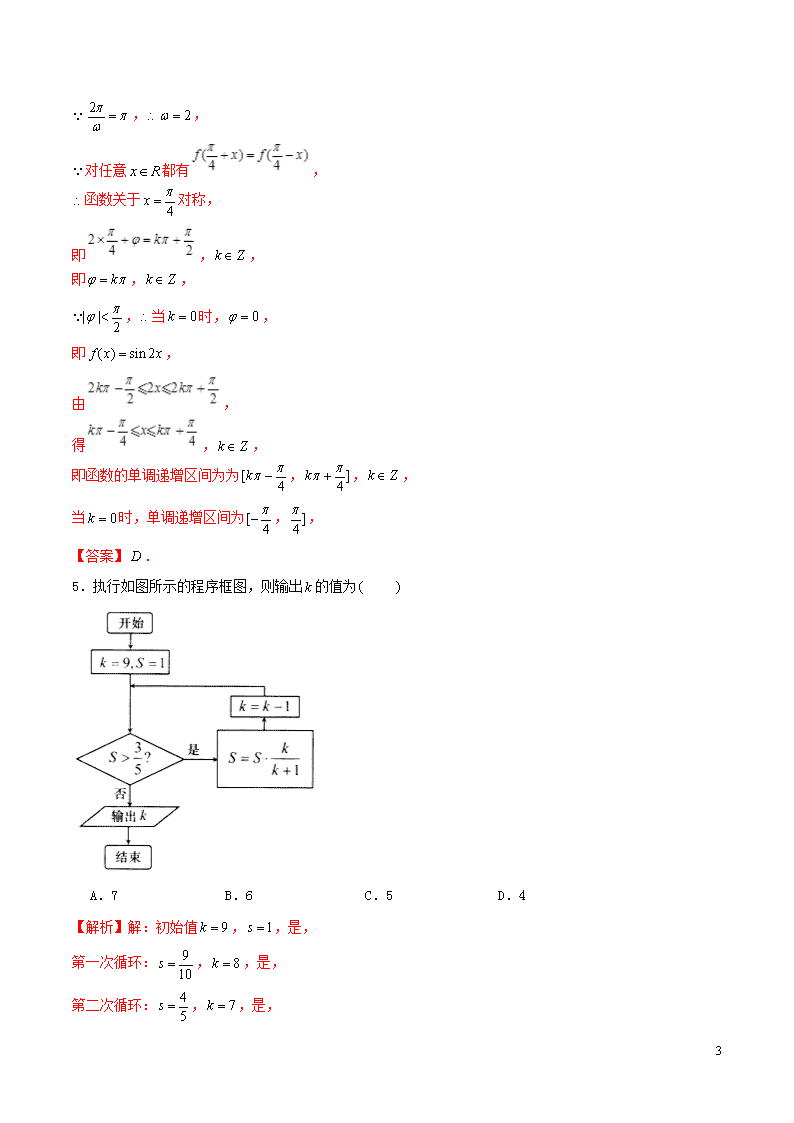5．执行如图所示的程序框图，则输出的值为　　‎ A．7 B．6 C．5 D．4‎ ‎【解析】解：初始值，，是，‎ 第一次循环：，，是，‎ 第二次循环：，，是，‎ 19‎ 第三次循环：，，是，‎ 第四次循环：，，否，输出．‎ ‎【答案】． 6．过抛物线的焦点作倾斜角为的直线，若与抛物线交于，两点，且的中点到抛物线准线的距离为4，则的值为　　‎ A． B．1 C．2 D．3‎ ‎【解析】解：设，，，，则，‎ ‎①②，得：，‎ ‎，‎ 过抛物线的焦点且斜率为1的直线与抛物线相交于，两点，‎ ‎，方程为：，‎ 为中点纵坐标，‎ ‎，‎ ‎，，‎ ‎，‎ ‎，‎ ‎，‎ 中点横坐标为，‎ 线段的中点到抛物线准线的距离为4，‎ ‎，解得．‎ ‎【答案】． 7．如图是一几何体的三视图，则该几何体的体积是　　‎ 19‎ A．9 B．10 C．12 D．18‎ ‎【解析】解：由三视图可知该几何体是底面是直角梯形，侧棱和底面垂直的四棱锥，‎ 其中高为3，底面直角梯形的上底为2，下底为4，梯形的高为3，‎ 所以四棱锥的体积为．‎ ‎【答案】． 8．已知双曲线的左，右焦点分别为，，点在双曲线上，且，，成等差数列，则该双曲线的方程为　　‎ A． B． C． D．‎ ‎【解析】解：设，，．‎ ‎．‎ ‎，，成等差数列，．‎ ‎，，‎ 联立解得，，．‎ 双曲线的标准方程为：．‎ ‎【答案】． 9．如图所示，三国时代数学家在《周脾算经》中利用弦图，给出了勾股定理的绝妙证明．图中包含四个全等的直角三角形及一个小正方形（阴影），设直角三角形有一个内角为，若向弦图内随机抛掷200颗米粒（大小忽略不计，取，则落在小正方形（阴影）内的米粒数大约为　　‎ 19‎ A．20 B．27 C．54 D．64‎ ‎【解析】解：设大正方体的边长为，则小正方体的边长为，‎ 设落在小正方形内的米粒数大约为，‎ 则，解得：‎ ‎【答案】． 10．如果点满足，点在曲线上，则的取值范围是　　‎ A．， B．， C．， D．，‎ ‎【解析】解：曲线对应的圆心，半径，‎ 作出不等式组对应的平面区域如图：‎ 直线的斜率，‎ 则当位于点时，取得最小值，‎ 此时．最大值为：．‎ 则的取值范围是：，‎ ‎【答案】．‎ 19‎ ‎ 11．在四面体中，平面，，，若四面体的外接球的表面积为，则四面体的体积为　　‎ A． B．12 C．8 D．4‎ ‎【解析】解：在四面体中，平面，，，‎ 四面体的外接球的表面积为，‎ 四面体的外接球的半径，‎ 设四面体的外接球的球心为，则，‎ 过作平面，是垂足，过，交于，‎ 是的重心，‎ ‎，‎ ‎，‎ 四面体的体积为：‎ ‎．‎ ‎【答案】．‎ 19‎ ‎ 12．已知，曲线与有公共点，且在公共点处的切线相同，则实数的最小值为　　‎ A．0 B． C． D．‎ ‎【解析】解：设与在公共点，处的切线相同，‎ ‎，，‎ 由题意，，‎ 得，，‎ 由得或（舍去），‎ 即有．‎ 令，‎ 则，‎ 当，即时，；‎ 当，即时，．‎ 故在为减函数，在，为增函数，‎ 于是在的最小值为，‎ 19‎ 故的最小值为．‎ ‎【答案】．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分．‎ ‎13．复数满足，其中是虚数单位，则复数的模是　　．‎ ‎【解析】解：由，‎ 得．‎ 则复数的模是．‎ ‎【答案】． 14．的展开式中的系数为　　．（用数字作答）‎ ‎【解析】解：的展开式的通项公式为，‎ 令，求得，故展开式中的系数为，‎ ‎【答案】15． 15．已知变量，满足约束条件，则的最大值是　6　．‎ ‎【解析】解：变量，满足约束条件 的可行域如图阴影部分，‎ 由解得 目标函数可看做斜率为的动直线，‎ 其纵截距越大，越大，‎ 由图数形结合可得当动直线过点时，．‎ ‎【答案】6．‎ 19‎ ‎ 16．已知函数有两个零点，，若其导函数为，则下列4个结论中正确的为　①②④　（请将所有正确结论的序号填入横线上）．‎ ‎①；‎ ‎②；‎ ‎③；‎ ‎④．‎ ‎【解析】解：设，，得在单调递减，在，单调递增．‎ 当时，，且，；当时，（1）；‎ 当时，，且，；函数有两个零点，‎ 得且．故①正确，③错误．‎ 由在单调递减快，在，单调递增慢，所以．‎ 而，即而．，所以，故④正确．‎ 构造函数，，则，‎ 函数在单调递增，，从而，即，‎ ‎，因为，，，，在，单调递增，所以 19‎ ‎，即，所以①②④正确，③错误．‎ 故答案为①②④．‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17．已知数列满足，．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）令，数列的前项和为，求证：．‎ ‎【解析】（本小题满分12分）‎ 解：（Ⅰ）因为①‎ 当时，，‎ 当时，②‎ 由①②得：， ‎ 因为适合上式，所以 ‎ ‎（Ⅱ）证明：由（Ⅰ）知，‎ ‎，即． 18．已知四边形满足，，是的中点，将沿翻折成△，使面面，为的中点．‎ ‎（1）求四棱锥的体积；‎ ‎（2）证明：面；‎ ‎（3）求面与面所成锐二面角的余弦值．‎ 19‎ ‎【解析】（Ⅰ）解：取的中点，连接，因为，是的中点，‎ 所以为等边三角形，所以，‎ 又因为面面，所以面，‎ 所以 ‎（Ⅱ）证明：连接交于，连接，因为为菱形，，‎ 又为的中点，所以，‎ 因为面 所以面 ‎（Ⅲ）解：连接，分别以，，为，，轴，建立空间直角坐标系．‎ 则 设面的法向量，则，‎ 令，则 设面的法向量为，则，‎ 令，则 19‎ 则，‎ 所以二面角的余弦值为 ‎ 19．某校为了解校园安全教育系列活动的成效，对全校学生进行一次安全意识测试，根据测试成绩评定“合格”、“不合格”两个等级，同时对相应等级进行量化：“合格”记5分，“不合格”记0分．现随机抽取部分学生的成绩，统计结果及对应的频率分布直方图如下所示：‎ 等级 不合格 合格 得分 ‎，‎ ‎，‎ ‎，‎ ‎，‎ 频数 ‎6‎ ‎24‎ ‎（Ⅰ）若测试的同学中，分数段，、，、，、，内女生的人数分别为2人、8人、16人、4人，完成列联表，并判断：是否有以上的把握认为性别与安全意识有关？‎ ‎（Ⅱ）用分层抽样的方法，从评定等级为“合格”和“不合格”的学生中，共选取10人进行座谈，现再从这10人中任选4人，记所选4人的量化总分为，求的分布列及数学期望；‎ ‎（Ⅲ）某评估机构以指标，其中表示的方差）来评估该校安全教育活动的成效，若，则认定教育活动是有效的；否则认定教育活动无效，应调整安全教育方案．在（Ⅱ）的条件下，判断该校是否应调整安全教育方案？‎ 附表及公式：．‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ 19‎ 是否合格 性别 不合格 合格 总计 男生 女生 总计 ‎【解析】解：（Ⅰ）由频率分布直方图可知，得分在，的频率为，故抽取的学生答卷总数为，，．‎ 性别与合格情况的列联表为：‎ 是否合格 性别 不合格 合格 小计 男生 ‎14‎ ‎16‎ ‎30‎ 女生 ‎10‎ ‎20‎ ‎30‎ 小计 ‎24‎ ‎36‎ ‎60‎ 即在犯错误概率不超过的前提下，不能认为性别与安全测试是否合格有关．‎ ‎（Ⅱ）“不合格”和“合格”的人数比例为，因此抽取的10人中“不合格”有4人，“合格”有6人，所以可能的取值为20、15、10、5、0，‎ 19‎ ‎，．的分布列为：‎ ‎20‎ ‎15‎ ‎10‎ ‎5‎ ‎0‎ 所以． ‎ ‎（Ⅲ）由（Ⅱ）知：‎ ‎．‎ 故我们认为该校的安全教育活动是有效的，不需要调整安全教育方案． 20．已知中，，且．以边的中垂线为轴，以所在的直线为轴，建立平面直角坐标系．‎ ‎（Ⅰ）求动点的轨迹的方程；‎ ‎（Ⅱ）已知定点，不垂直于的动直线与轨迹相交于、两点，若直线、关于轴对称，求面积的取值范围．‎ ‎【解析】解：（Ⅰ）由得：，‎ 由正弦定理 所以点的轨迹是：以，为焦点的椭圆（除轴上的点），其中，，则，‎ 故轨迹的轨迹方程为． ‎ ‎（Ⅱ） 由题，由题可知，直线的斜率存在，设，，，，将直线的方程代入轨迹的方程得：．‎ 由△得，，且．‎ 19‎ 直线、关于轴对称，，即．‎ 化简得：，，得． ‎ 那么直线过点，，‎ 所以面积： ‎ 设，则，，显然，在上单调递减，‎ ‎． 21．设函数．‎ ‎（Ⅰ）求函数单调递减区间；‎ ‎（Ⅱ）若函数的极小值不小于，求实数的取值范围．‎ ‎【解析】解：（Ⅰ）由题可知，所以 由，解得或．‎ 综上所述，的递减区间为和．‎ ‎（Ⅱ）由题可知，所以．‎ ‎（1）当时，，则在为增函数，在为减函数，所以在上没有极小值，故舍去；‎ 19‎ ‎（2）当时，，由得，由于，所以，‎ 因此函数在为增函数，在为减函数，在为增函数，‎ 所以 即．‎ 令，则上述不等式可化为．‎ 上述不等式①‎ 设，则，故在为增函数．‎ 又（2），所以不等式①的解为，因此，所以，解得．综上所述，．‎ 考生注意：请在第22、23两题中任选一题作答，如果多做，则按所做的第一个题目计分.作答时，请用2B铅笔在答题卡上将所选题目后的方框涂黑．[选修4-4：坐标系与参数方程 22．设极坐标系与直角坐标系有相同的长度单位，原点为极点，轴正半轴为极轴，曲线的参数方程为是参数），直线的极坐标方程为．‎ ‎（Ⅰ）求曲线的普通方程和直线的参数方程；‎ ‎（Ⅱ）设点，若直线与曲线相交于，两点，且，求的值 ‎【解析】解：（Ⅰ）由题可得，曲线的普通方程为．‎ 直线的直角坐标方程为，即 由于直线过点，倾斜角为，‎ 19‎ 故直线的参数方程是参数）‎ ‎（注意：直线的参数方程的结果不是唯一的．‎ ‎（Ⅱ）设、两点对应的参数分别为、，将直线的参数方程代入曲线的普通方程并化简得：． ‎ 所以，解得． ‎ ‎[选修4-5：不等式选讲] 23．已知．‎ ‎（Ⅰ）关于的不等式恒成立，求实数的取值范围；‎ ‎（Ⅱ）若，且，求的取值范围．‎ ‎【解析】（本小题满分10分）选修：不等式选讲 解：（Ⅰ），所以，‎ 恒成立，则，‎ 解得．‎ ‎（Ⅱ），，，‎ 则， ‎ 又，所以，于是，‎ 故． ‎ 19‎ 19‎