- 1.32 MB
- 2021-04-17 发布
“合肥市一、六、八、168中学”2015年高三
四校联考最后一卷(理科数学)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知为虚数单位,复数,则复数在复平面内的对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知实数满足且成等比数列,则有
A.最大值 B.最大值 C.最小值 D.最小值
3.下列三种说法中:①命题“”的否定是“”②“命题为真”是“命题为真”的必要而不充分条件;③“若,则的逆命题为真”其中错误的是
A.③ B. ①②
C.①③ D.②
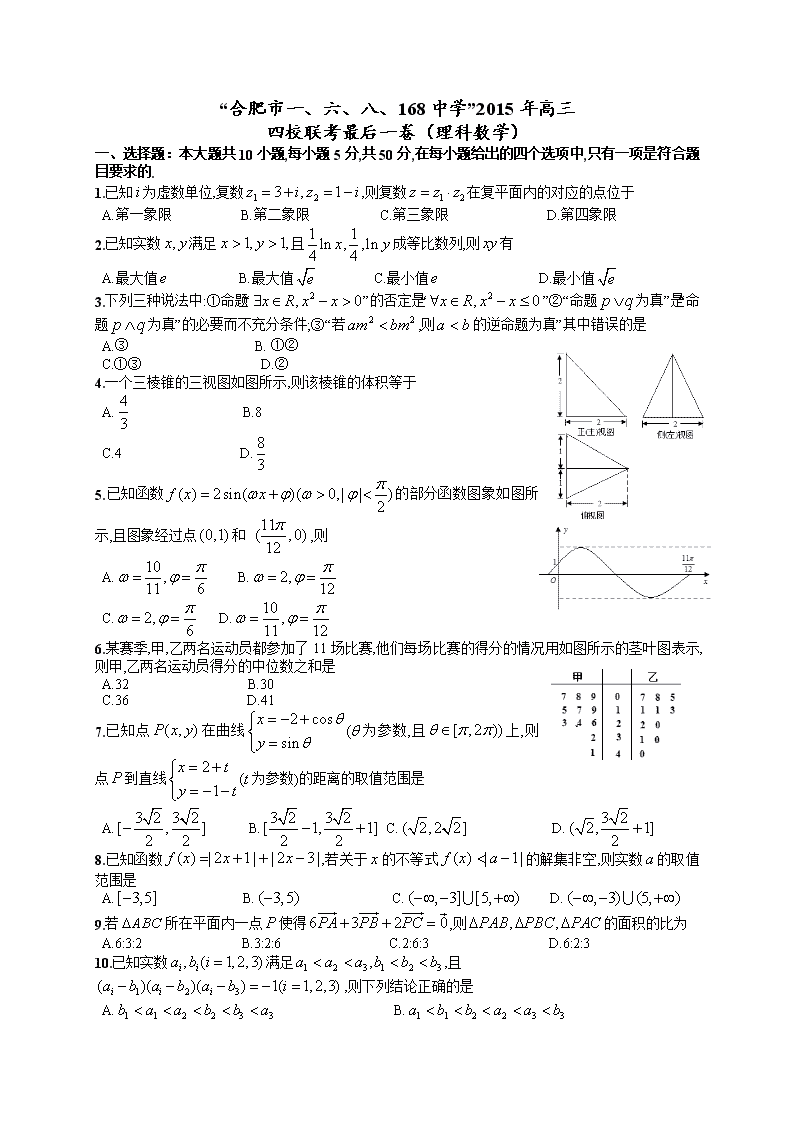
4.一个三棱锥的三视图如图所示,则该棱锥的体积等于
A. B.8
C.4 D.
5.已知函数的部分函数图象如图所示,且图象经过点和 ,则
A. B.
C. D.
6.某赛季,甲,乙两名运动员都参加了11场比赛,他们每场比赛的得分的情况用如图所示的茎叶图表示,则甲,乙两名运动员得分的中位数之和是
A.32 B.30
C.36 D.41
7.已知点在曲线为参数,且上,则点到直线为参数)的距离的取值范围是
A. B. C. D.
8.已知函数,若关于的不等式的解集非空,则实数的取值范围是
A. B. C. D.
9.若所在平面内一点使得,则的面积的比为
A.6:3:2 B.3:2:6 C.2:6:3 D.6:2:3
10.已知实数满足,且
,则下列结论正确的是
A. B.
C. D.
二、填空题:本大题共5小题,每小题5分,共25分,请将答案填在答题卡的相应位置.
11.二项式的展开式中,含项的系数为
12.由计算机产生的两个0到1上的随机数,按右侧流程图所示的规则,则能输出数对的概率是
13.已知为直角三角形,是斜边,三个顶点在平面的同侧, 在平面内的正投影为
正,且,则的面积是
14.我们把焦点相同且离心率互为倒数的椭圆和双曲线称为一对“合一曲线”,已知是一对“合一曲线”的焦点,是他们在第一象限的交点,当时,这一对“合一曲线”中椭圆的离心率为
15.已知函数,给出下列命题:
①函数为偶函数;②函数是周期函数; ③存在,使得为顶点的三角形是等边三角形;④存在,使得为顶点的三角形是等腰直角三角形.其中的真命题是 (填上你认为正确的所有命题的序号)
三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16(本小题满分12分)
在中,角所对的边分别为.且.
(Ⅰ)求;
(Ⅱ)求.
17(本小题满分12分)
合肥八中模拟联合国协会共有三个小组:中文组,英文组,辩论组,现有12名新同学(其中3名为男同学)被平均分配到三个小组.
(Ⅰ)求男同学甲被分到中文组,其他2名男同学被分到另外两个不同小组的概率;
(Ⅱ)若男同学所在的小组个数为,求的概率分布列及数学期望.
18(本小题满分12分)
如图,在三棱锥中,为等边三角形,平面为上的动点.
(Ⅰ)若当与平面所成的角最大时,求二面角的正切值;
(Ⅱ)若在平面上的射影为的重心,求三棱锥的外接球的体积.
19(本小题满分13分)
已知为一定点,是轴上的一动点,轴上的点满足,点满足
.
(Ⅰ)求点的轨迹曲线的方程;
(Ⅱ)过直线的点作曲线的切线,切点分别为,求证:当点在直线上运动时,直线恒过定点.
20(本小题满分13分)
已知,函数.
(Ⅰ)若,求函数的单调区间;
(Ⅱ)若有两个相异的零点,求证:.
21(本小题满分12分)
已知数列满足.
(Ⅰ)求证:;
(Ⅱ)在数列中任意取定一项,构造数列,满足,问:数列是有穷数列还是无穷数列?并证明你的结论;
(Ⅲ)令,求证:
相关文档
- 2020届高考化学一轮复习化学物质及2021-04-17 03:00:149页
- 高考试题——天津卷理综生物部分有2021-04-17 03:00:095页
- 高考地理选做题练习卷答案2021-04-17 02:59:526页
- 2016高考生物二轮专题集训2021-04-17 02:59:426页
- 2014高考数学题库精选核心考点大冲2021-04-17 02:59:3231页
- 安徽省安庆市桐城市某中学2019-2022021-04-17 02:59:1622页
- 2009年高考英语(江苏卷)-Word版含2021-04-17 02:58:1510页
- 2020版高考地理一轮复习 课后限时2021-04-17 02:58:055页
- 2018版高考数学(理)(人教)大一轮复习文2021-04-17 02:57:5617页
- 2020届高考地理新探究大一轮检测:第2021-04-17 02:57:496页