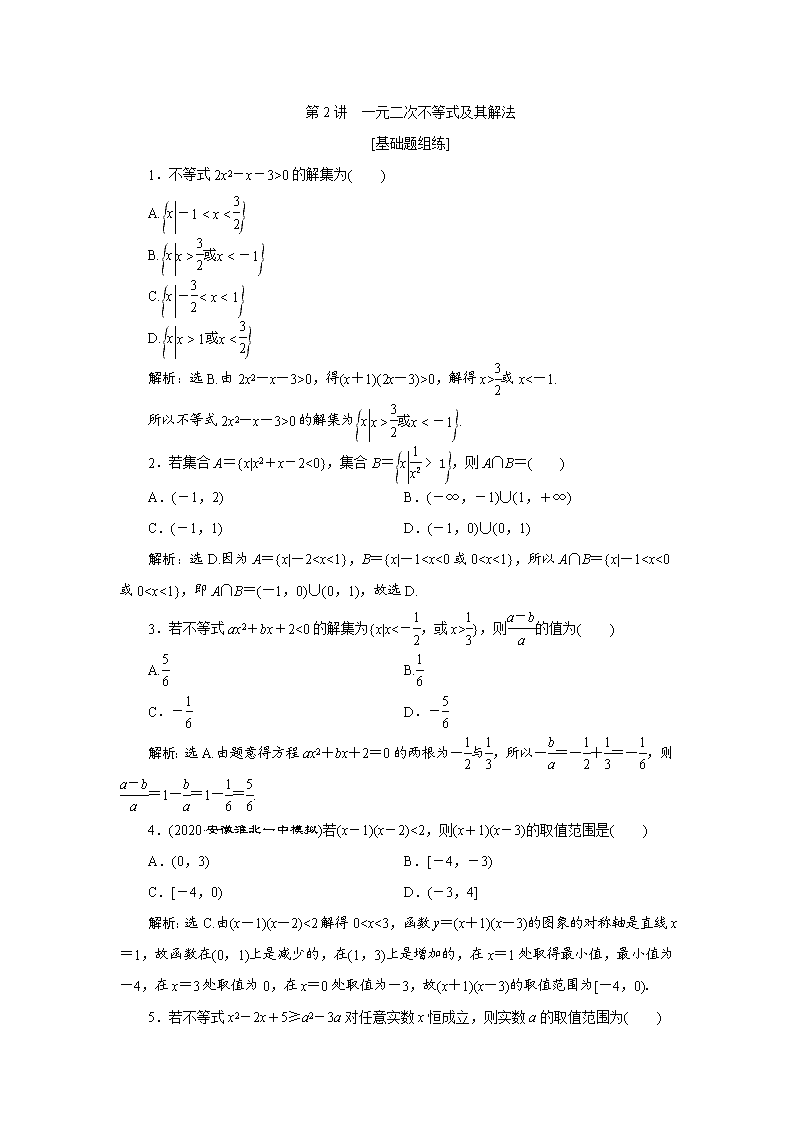【数学】2021届一轮复习北师大版（文）第七章　第2讲　一元二次不等式及其解法作业 5页

下载文档

106.00 KB
2021-04-17 发布

【数学】2021届一轮复习北师大版（文）第七章　第2讲　一元二次不等式及其解法作业

5页
当前文档由用户上传发布，收益归属用户
下载文档

第2讲　一元二次不等式及其解法 ‎[基础题组练]‎ ‎1．不等式2x2－x－3>0的解集为(　　)‎ A. B. C. D. 解析：选B.由2x2－x－3>0，得(x＋1)(2x－3)>0，解得x>或x<－1.‎ 所以不等式2x2－x－3>0的解集为.‎ ‎2．若集合A＝{x|x2＋x－2<0}，集合B＝，则A∩B＝(　　)‎ A．(－1，2)　　　　　　　 B．(－∞，－1)∪(1，＋∞)‎ C．(－1，1) D．(－1，0)∪(0，1)‎ 解析：选D.因为A＝{x|－2}，则的值为(　　)‎ A. B. C．－ D．－解析：选A.由题意得方程ax2＋bx＋2＝0的两根为－与，所以－＝－＋＝－，则＝1－＝1－＝.‎ ‎4．(2020·安徽淮北一中模拟)若(x－1)(x－2)<2，则(x＋1)(x－3)的取值范围是(　　)‎ A．(0，3) B．[－4，－3)‎ C．[－4，0) D．(－3，4]‎ 解析：选C.由(x－1)(x－2)<2解得0x(x－2)的解集是．‎ 解析：不等式|x(x－2)|>x(x－2)的解集即x(x－2)<0的解集，解得00的解集是．‎ 解析：原不等式可化为(x－a)<0，由00的解集是.‎ ‎(1)求实数a的值；‎ ‎(2)求不等式ax2－5x＋a2－1>0的解集．‎ 解：(1)由题意知a<0，且方程ax2＋5x－2＝0的两个根为，2，代入方程解得a＝－2.‎ ‎(2)由(1)知不等式ax2－5x＋a2－1>0，‎ 即为－2x2－5x＋3>0，即2x2＋5x－3<0，解得－30的解集为.‎ ‎10．函数f(x)＝x2＋ax＋3.‎ ‎(1)当x∈R时，f(x)≥a恒成立，求实数a的取值范围；‎ ‎(2)当x∈[－2，2]时，f(x)≥a恒成立，求实数a的取值范围．‎ 解：(1)因为当x∈R时，x2＋ax＋3－a≥0恒成立，‎ 需Δ＝a2－4(3－a)≤0，即a2＋4a－12≤0，‎ 所以实数a的取值范围是[－6，2]．‎ ‎(2)当x∈[－2，2]时，设g(x)＝x2＋ax＋3－a≥0恒成立，分如下三种情况讨论(如图所示)：‎ ‎①如图①，当g(x)的图象恒在x轴或x轴上方且满足条件时，有Δ＝a2－4(3－a)≤0，即－6≤a≤2.‎ ‎②如图②，g(x)的图象与x轴有交点，‎ 但当x∈[－2，＋∞)时，g(x)≥0，‎ 即即可得解得a∈∅.‎ ‎③如图③，g(x)图象与x轴有交点，但当x∈(－x，2]时，g(x)≥0.即即可得所以－7≤a≤－6.‎ 综上，实数a的取值范围是[－7，2]．‎ ‎　‎ ‎[综合题组练]‎ ‎1．若关于x的不等式x2－(a＋1)x＋a<0的解集中，恰有3个整数，则实数a的取值范围是(　　)‎ A．(4，5) B．(－3，－2)∪(4，5)‎ C．(4，5] D．[－3，－2)∪(4，5]‎ 解析：选D.将不等式x2－(a＋1)x＋a<0化为(x－1)(x－a)<0.当a>1时，得10)有两个实根x1，x2.‎ ‎(1)求(1＋x1)(1＋x2)的值；‎ ‎(2)求证：x1<－1且x2<－1；‎ ‎(3)如果∈，试求a的取值范围．‎ 解：(1)因为关于x的一元二次方程ax2＋x＋1＝0(a>0)有两个实根x1，x2.‎ 所以x1＋x2＝－，x1x2＝，‎ 则(1＋x1)(1＋x2)＝1＋x1＋x2＋x1·x2＝1－＋＝1.‎ ‎(2)证明：由Δ≥0，得00，‎ 所以f(x)的图象与x轴的交点均位于点(－1，0)的左侧，‎ 故x1<－1且x2<－1.‎ ‎(3)由⇒＝＋＋2＝.‎ 因为∈，所以＝＋＋2∈⇒a∈.‎ 又⇒0

【数学】2021届一轮复习北师大版（文）第七章　第2讲　一元二次不等式及其解法作业 5页