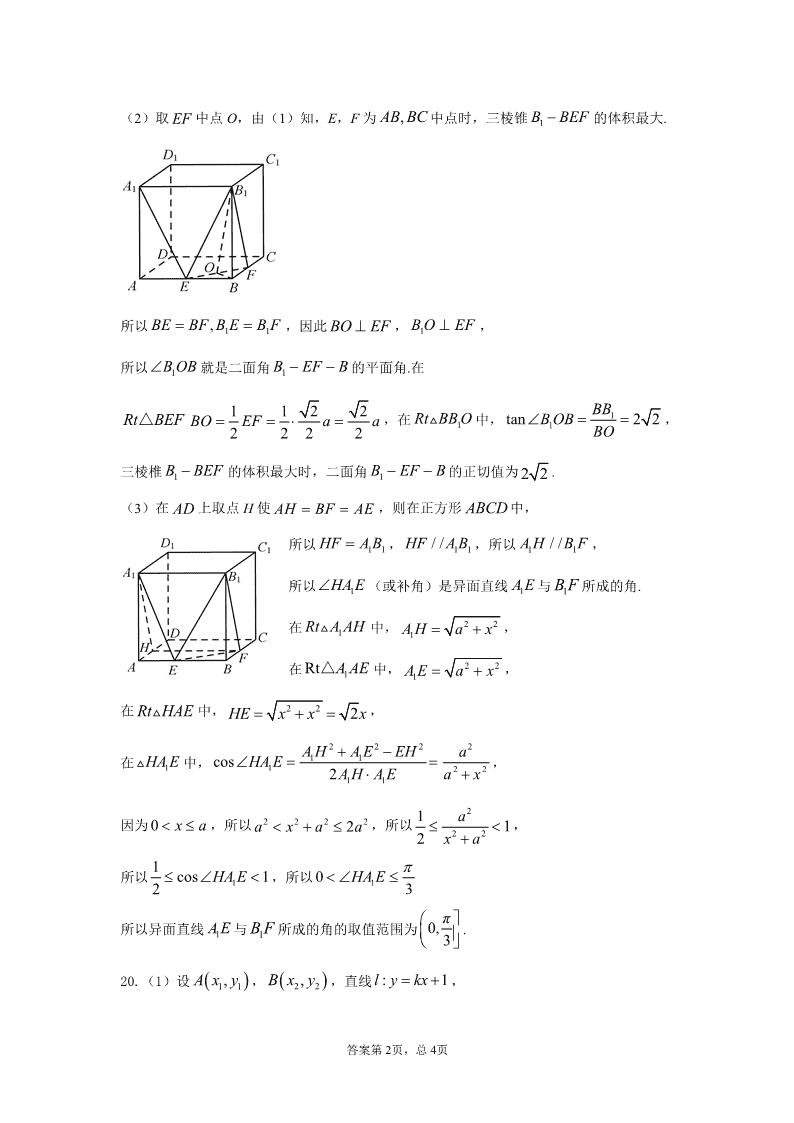2020-2021学年高三上学期月考数学（理）答案（四川省成都市新都一中） 4页

答案第 1页，总 4页 高三月考（理科）参考答案 一、选择题 1．D 2．D 3．B 4．D 5．C 6．C 7．A 8．A 9．D 10．A 11．D12．C 二、填空题 13． 2 i  14． 2 2 7 3a  15． 16． 3 3,3 3    三、解答题 17．（1）由题意可知，  1 4 4 4 242 a aS   ， 1 4 12a a   . 又 1 4 27a a  ， 0d  ， 1 3a  ， 4 9a  ， 2d  ， 2 1na n   .故数列 na 的通项公式为 2 1na n  . （2）由（1）可知，   1 1 1 2 1 2 3n n n b a a n n     1 1 1 2 2 1 2 3n n       ， 1 1 1 1 1 1 1 1 1 1 2 3 5 5 7 2 1 2 3 2 3 2 3 6 9n nT n n n n                       . 18． （Ⅰ） 0.005 0.01 0.03 0.035 10 1a      ， 0.02a  ． （Ⅱ）第 3 组人数为100 0.3 30  人，第 4 组人数为 0.2 100 20  人， 第5 组人数为 0.1 100 10  人，∴比例为3: 2:1，∴第 3 组，4 组，5 组各抽 3 ，2 ，1人． （Ⅲ）记 3 组人为 1A ， 2A ， 3A ， 4 组人为 1B ， 2B ， 5 组人为 1C ，共有 2 6 15C  种， 符合有： 1 1A B  1 2A B  2 1A B  2 2A B  3 1A B  3 2A B  1 2B B  1 1,B C  2 1,B C 9 种，∴ 9 3 15 5P   ． 19． 解：（1）因为正方体 1 1 1 1ABCD A B C D ，所以 1BB  平面 ABCD 所以  1 2 2 21 1 ( ) ( )3 2 6 6 6 2 4B BEF a a a a aV a x x a a x x x ax x                      ， 当 2 ax  时，三棱锥 1B BEF 的体积最大. 答案第 2页，总 4页 （2）取 EF 中点 O，由（1）知，E，F 为 ,AB BC 中点时，三棱锥 1B BEF 的体积最大. 所以 1 1,BE BF B E B F  ，因此 BO EF ， 1B O EF ， 所以 1B OB 就是二面角 1B EF B  的平面角.在 Rt BEF△ 1 1 2 2 2 2 2 2BO EF a a    ，在 1Rt BB O 中， 1 1tan 2 2BBB OB BO    ， 三棱椎 1B BEF 的体积最大时，二面角 1B EF B  的正切值为 2 2 . （3）在 AD 上取点 H 使 AH BF AE  ，则在正方形 ABCD 中， 所以 1 1HF A B ， 1 1/ /HF A B ，所以 1 1/ /A H B F ， 所以 1HA E （或补角）是异面直线 1A E 与 1B F 所成的角. 在 1Rt A AH 中， 2 2 1A H a x  ， 在 1Rt A AE△ 中， 2 2 1A E a x  ， 在 Rt HAE 中， 2 2 2HE x x x   ， 在 1HA E 中， 2 2 2 2 1 1 1 2 2 1 1 cos 2 A H A E EH aHA E A H A E a x      ， 因为 0 x a  ，所以 2 2 2 22a x a a   ，所以 2 2 2 1 12 a x a   ， 所以 1 1 cos 12 HA E   ，所以 10 3HA E    所以异面直线 1A E 与 1B F 所成的角的取值范围为 0, 3 π     . 20.（1）设  1 1,A x y ，  2 2,B x y ，直线 : 1l y kx  ， 答案第 3页，总 4页 所以 2 4 1 x y y kx      得 2 4 4 0x kx   ，所以 1 2 1 2 4 4 x x k x x      由 2 14 2x y y x   ，所以  1 1 1 1 1 2:l y y x x x   ， 即： 2 1 1 1 1 2 4: xl y x x  ， 同理 2 2 2 2 1: 2 4 xl y x x  ，联立得 1 2 0 1 2 0 22 14 x xx k x xy        ，即 0 1y   . （2）因为 1 2 , 22 x xQF       ，  2 1 2 1,AB x x y y   ， 所以  2 2 2 2 2 2 2 22 1 2 1 2 1 2 12 02 2 2 x x x x x xQF AB y y          ， 所以 QF AB  ，即 MN AB ，   2 1 2 1 22 4 4 4AB y y k x x k        ， 同理 2 4 4MN k   ，  2 2 2 2 1 1 18 1 1 8 2 322AMBNS AB MN k kk k                  ， 当且仅当 1k   时，四边形 AMBN 面积的最小值为 32 . 21．（I）   ln 2 4f x x ax   ． ∴  f x 在 0,  内单调递减， ∴   ln 2 4 0f x x ax    在 0,  内恒成立， 即 ln 24 xa x x   在 0,  内恒成立． 令   ln 2xg x x x   ，则   2 1 ln xg x x    ， ∴当 10 ex  时，   0g x  ，即  g x 在 10, e      内为增函数； 当 1x e  时，   0g x  ，即  g x 在 1 ,e     内为减函数． ∴  g x 的最大值为 1g ee      ， ∴ e ,4a     （Ⅱ）若函数  f x 有两个极值点分别为 1x ， 2x ， 答案第 4页，总 4页 则   ln 2 4 0f x x ax    在 0,  内有两根 1x ， 2x ， 由（I），知 e0 4a  ． 由 1 1 2 2 ln 2 4 0 ln 2 4 0 x ax x ax        ，两式相减，得  1 2 1 2ln ln 4x x a x x   ． 不妨设 1 20 x x  ， ∴要证明 1 2 1 2x x a   ，只需证明     1 2 1 2 1 2 1 4 2 ln ln x x a x x a x x    ． 即证明  1 2 1 2 1 2 2 ln lnx x x xx x    ，亦即证明 1 2 1 1 2 2 2 1 ln 1 x x x x x x        ． 令函数 10,ln1 )1(2)(   xxx xxh ∴ 2 2 ( 1)'( ) 0( 1) xh x x x    ，即函数  h x 在 0,1 内单调递减． ∴  0,1x 时，有    1 0h x h  ，∴ 2( 1) ln1 x xx   ． 即不等式 1 2 1 1 2 2 2 1 ln 1 x x x x x x        成立． 综上，得 1 2 1 2x x a   ． 22．（1） 1C 的参数方程为 cos 3 sin x y     （  为参数）； l 的直角坐标方程为 0x y  . （2）由题设 ( 2,0)P  ，由（1）可设 (cos , 3sin )Q   ，于是 1 31 cos , sin2 2M        . M 到直线l 距离 1 31 cos sin 1 cos2 2 3 2 2 d             ， 当 2 3   时， d 取最大值 2 ，此时点Q 的直角坐标为 1 3,2 2     .