- 581.50 KB
- 2021-04-17 发布
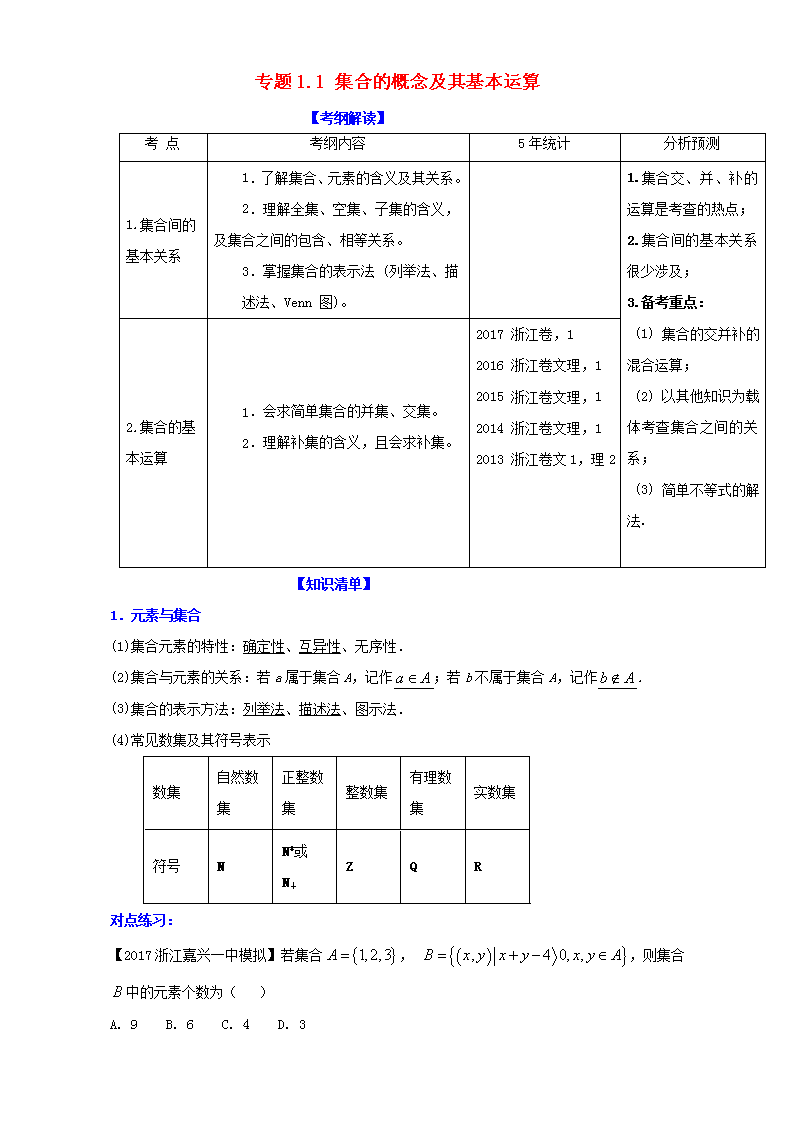
专题1.1 集合的概念及其基本运算
【考纲解读】
考 点
考纲内容
5年统计
分析预测
1.集合间的基本关系
1. 了解集合、元素的含义及其关系。
2.理解全集、空集、子集的含义,及集合之间的包含、相等关系。
3.掌握集合的表示法 (列举法、描述法、Venn 图)。
1.集合交、并、补的运算是考查的热点;
2.集合间的基本关系很少涉及;
3.备考重点:
(1) 集合的交并补的混合运算;
(2) 以其他知识为载体考查集合之间的关系;
(3) 简单不等式的解法.
2.集合的基本运算
1.会求简单集合的并集、交集。
2.理解补集的含义,且会求补集。
2017 浙江卷,1
2016 浙江卷文理,1
2015 浙江卷文理,1
2014 浙江卷文理,1
2013 浙江卷文1,理2
【知识清单】
1.元素与集合
(1)集合元素的特性:确定性、互异性、无序性.
(2)集合与元素的关系:若a属于集合A,记作;若b不属于集合A,记作.
(3)集合的表示方法:列举法、描述法、图示法.
(4)常见数集及其符号表示
数集
自然数集
正整数集
整数集
有理数集
实数集
符号
N
N*或
N+
Z
Q
R
对点练习:
【2017浙江嘉兴一中模拟】若集合, ,则集合中的元素个数为( )
A. 9 B. 6 C. 4 D. 3
【答案】D
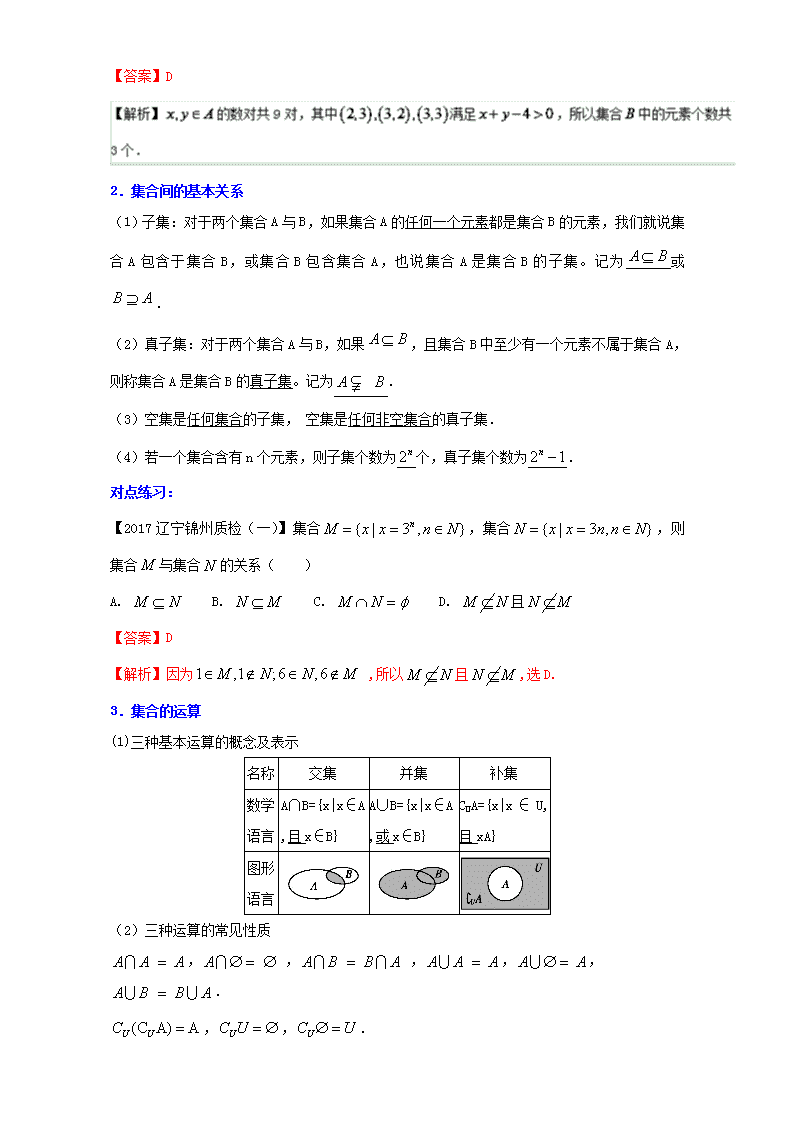
2.集合间的基本关系
(1)子集:对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,我们就说集合A包含于集合B,或集合B包含集合A,也说集合A是集合B的子集。记为或.
(2)真子集:对于两个集合A与B,如果,且集合B中至少有一个元素不属于集合A,则称集合A是集合B的真子集。记为.
(3)空集是任何集合的子集, 空集是任何非空集合的真子集.
(4)若一个集合含有n个元素,则子集个数为个,真子集个数为.
对点练习:
【2017辽宁锦州质检(一)】集合,集合,则集合与集合的关系( )
A. B. C. D. 且
【答案】D
【解析】因为 ,所以且,选D.
3.集合的运算
(1)三种基本运算的概念及表示
名称
交集
并集
补集
数学
语言
A∩B={x|x∈A,且x∈B}
A∪B={x|x∈A,或x∈B}
CUA={x|x∈U,且xA}
图形
语言
(2)三种运算的常见性质
, , ,,,.
,,.
, , , .
对点练习:
【2017浙江卷】已知,,则
A. B. C. D.
【答案】A
【考点深度剖析】
高考对集合知识的考查要求较低,均是以小题的形式进行考查,要求考生熟练掌握与集合有关的基础知识,集合的基本运算.纵观近5年的高考试题,主要考查集合的基本运算,其中集合以描述法呈现,元素的性质以不等式为主,偶有离散元素呈现.解决这类问题的关键在于正确理解集合中元素所具有属性的,明确集合中含有的元素,进一步进行交、并、补等运算.
【重点难点突破】
考点1 集合的概念
【1-1】若,集合,求的值________.
【答案】2
【解析】由可知,则只能,则有以下对应关系:
① 或 ②
由①得符合题意;②无解.
∴.
【1-2】集合,则中元素的个数为( )
A. 1个 B.2个 C.3个 D.4个
【答案】D
【解析】
试题分析:,,因为,∴集合,则中元素的个数为个.
【领悟技法】
与集合元素有关问题的思路:
(1)确定集合的元素是什么,即确定这个集合是数集还是点集.
(2)看这些元素满足什么限制条件.
(3)根据限制条件列式求参数的值或确定集合元素的个数,但要注意检验集合是否满足元素的互异性.
【触类旁通】
【变式一】【2017河北唐山期末】已知集合,则中元素的个数是( )
A. B. C. D.
【答案】B
【变式二】设P、Q为两个非空集合,定义集合.若,则中元素的个数是( )
A.9 B.8 C.7 D.6
【答案】B
【解析】=,故中元素的个数是8.
考点2 集合间的基本关系
【2-1】【2017四川适应性测试】设集合,集合,则使得的的所有取值构成的集合是( )
A. B. C. D.
【答案】D
【解析】:因为,所以,因此,选D.
【2-2】已知集合,,若,则实数的取值范围是( )
A.(0,1] B.1,+∞) C.(0,1) D.(1,+∞)
【答案】 B
【领悟技法】
1.判断两集合的关系常用两种方法:一是化简集合,从表达式中寻找两集合间的关系;二是用列举法表示各集合,从元素中寻找关系.
2.已知两集合间的关系求参数时,关键是将两集合间的关系转化为元素间的关系,进而转化为参数满足的关系,解决这类问题常常运用数轴、Venn图帮助分析.
【触类旁通】
【变式1】设集合,对任意实数x恒成立,且,则下列关系中成立的是( )
A. B. C. D.
【答案】A
【解析】,或.
∴.∴.∴.
【变式2】已知集合,集合,则( )
A. B. C. D.
【答案】B
【解析】,或,所以.
考点3 集合的基本运算
【3-1】【2017新课标1】已知集合A=,B=,则
A.AB= B.AB
C.AB D.AB=R
【答案】A
【解析】由得,所以,选A.
【3-2】【2017浙江五校联考】设全集,集合则集合= ( )
A. B.
C. D.
【答案】D
【3-3】【2017浙江台州一模】若集合,则 ( )
A. B. C. D.
【答案】C
【解析】,所以 或 ,故选C.
【领悟技法】
1. 集合的运算要注意灵活运用韦恩图和数轴,一般情况下,有限集的运算用维恩图分析,无限集的运算用数轴,这实际上是数形结合的思想的具体运用。
2. 涉及集合(交、并、补)运算,不要遗忘了空集这个特殊的集合。空集是任何集合的子集,是任何非空集合的真子集。
3. 有些集合是可以化简的,如果先化简再研究 其关系并进行运算,可使问题变得简单明了,易于解决.
【触类旁通】
【变式一】【2017浙江湖州、衢州、丽水4月联考】已知集合, 则=( )
A. -1,2) B. (-2,2) C. (-2,3] D. -1,3]
【答案】A
【解析】,所以,故选A.
【变式2】【2017浙江杭州二模】设,集合,则( )
A. B. C. D.
【答案】B
【易错试题常警惕】
易错典例1:设集合,,若,则的取值范围为________.
易错分析:忽视端点.
正确解析:由得,∴,由得,∴.
又当时,满足,时,也满足,∴.
温馨提示:利用数轴处理集合的交集、并集、补集运算时,要注意端点是实心还是空心,在含有参数时,要注意验证区间端点是否符合题意.
易错典例2:设集合,若,则实数的取值范围是_______.
易错分析:遗忘空集.
温馨提示:在中容易忽视集合这一情况,预防出现错误的方法是要注意分类讨论.
【素养提升之思想方法篇】
化抽象为具体——数形结合思想
数形结合思想,其实质是将抽象的数学语言与直观的图形结合起来,使抽象思维与形象思维相结合,使问题化难为易、化抽象为具体.数形结合思想在集合中的应用具体体现在以下三个方面:
(1)利用Venn图,直观地判断集合的包含或相等关系.
(2)利用Venn图,求解有限集合的交、并、补运算.
(3)借助数轴,分析无限集合的包含或相等关系或求解集合的交、并、补运算结果及所含参变量的取值范围问题.
【典例】已知集合,集合,且,则=________,=________.
【答案】 -1,1.
【解析】 由题意,知.因为,
,结合数轴,如图.
所以.