陕西省渭南市韩城市2020届高三（6月份）高考数学（文科）模拟试题 Word版含解析 20页

- 1 - 2020 年陕西省渭南市韩城市高考数学模拟试卷（文科）（6 月 份） 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分在每小题给出的四个选项 中，只有一项是符合题目要求的. 1.已知 是虚数单位，则 （ ） A. B. C. D. 【答案】A 【解析】 【分析】 利用复数的除法运算即可求解. 【详解】 . 故选：A 【点睛】本题考查了复数的除法运算，属于基础题. 2.已知集合 ， ，那么 ( ) A. B. C. D. 【答案】D 【解析】 【分析】 先化简集合 A，再利用交集的定义求解. 【详解】∵ ， ， ∴ . 故选：D. 【点睛】本题主要考查集合的基本运算，还考查了运算求解的能力，属于基础题. 3.已知双曲线 离心率为 则 b 的值为（ ）的 i 2 1 i i =+ 1 i+ 1 i− + 1 i− 2 2i− ( ) ( )( ) 2 2 12 2 2 11 1 1 1 i ii i ii i i i − += = = ++ + − − { }1 0A x x= − > { }1,0,1,2B = − A B = { }1,0− { }0,1 { }1,0,1,2- { }2 { }1A x x= > { }1,0,1,2B = − { }2A B∩ = 2 2 2 1( 0)yx bb − = > 5, - 2 - A. 1 B. 2 C. 3 D. 4 【答案】B 【解析】 【分析】 由题知 ， 及 联解可得. 【详解】由题知 ， ， ， . 故选：B. 【点睛】本题考查利用双曲线离心率求双曲线方程. 求双曲线方程的思路: (1)如果已知双曲线的中心在原点，且确定了焦点在 轴上或 轴上，则 设出相应形式的标准方程，然后根据条件确定关于 的方程组，解出 ，从而写 出双曲线的标准方程(求得的方程可能是一个，也有可能是两个，注意合理取舍，但不要漏 解)． (2)当焦点位置不确定时，有两种方法来解决：一种是分类讨论，注意考虑要全面；另一种是 设双曲线的一般方程为 求解． 4.若 ,则下列结论不正确的是（ ） A. B. C. D. 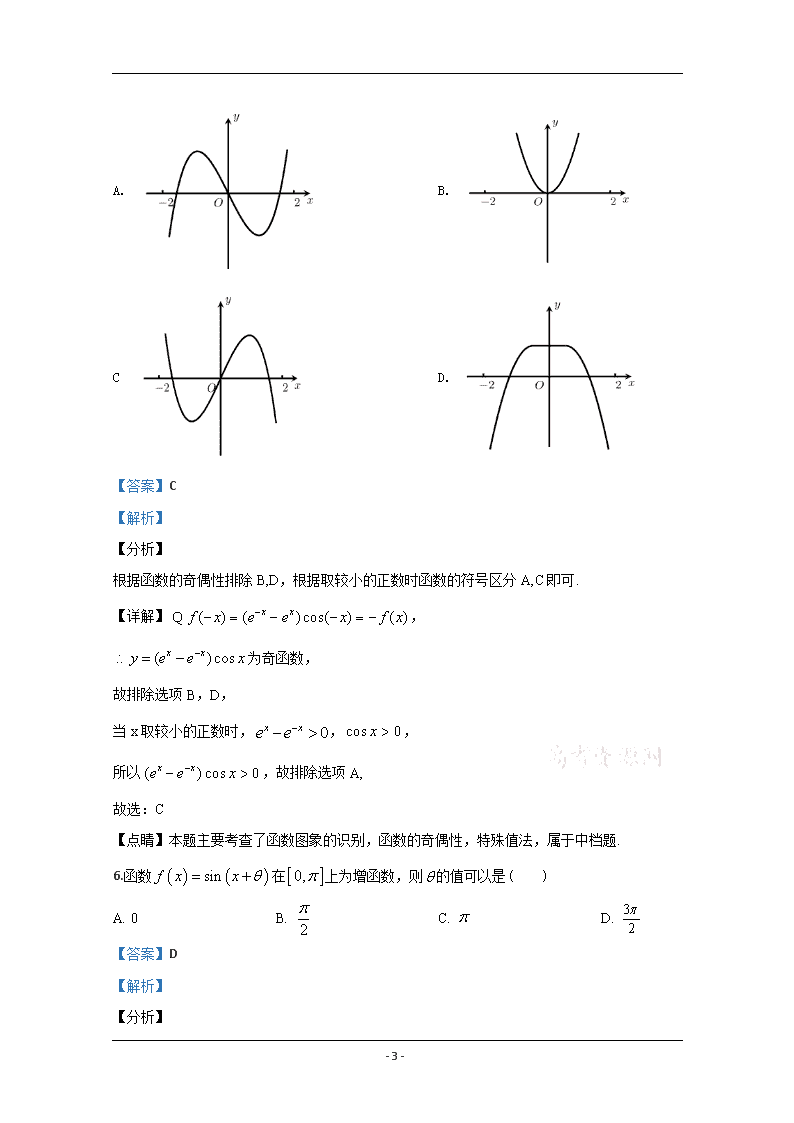【答案】C 【解析】 【分析】 利用不等式的基本性质、特殊值法即可得出． 【详解】 ， ， ，由函数 在 上单调递增，可得： ． 设 ， 时， 与 矛盾． 因此只有 错误． 故选： ． 【点睛】本题考查不等式的性质、特殊值法，属于基础题． 5.函数 y＝（ex﹣e﹣x）•cosx 的图象大致为（ ） 2 1a = 5ce a = = 2 2 2+c a b= 2 1a = 5ce a = = 2 2 2 2 2 2 + 5c a be a a= = = 2b∴ = x y a b c， ， 2 2a b， 2 2 1( 0)mx ny mn+ = < 0b a< < 1 1 a b < 2ab a> | | | | | |a b a b+ > + 3 3a b> 0b a< < ∴ 1 1 a b < 2ab a> 3y x= R 3 3a b> 1a = − 2b = − | | | | | |a b a b+ = + C C C - 3 - A. B. C D. 【答案】C 【解析】 【分析】 根据函数的奇偶性排除 B,D，根据取较小的正数时函数的符号区分 A,C 即可. 【详解】 ， 为奇函数， 故排除选项 B，D， 当 x 取较小的正数时， ， ， 所以 ，故排除选项 A, 故选：C 【点睛】本题主要考查了函数图象的识别，函数的奇偶性，特殊值法，属于中档题. 6.函数 在 上为增函数，则 的值可以是( ) A. 0 B. C. D. 【答案】D 【解析】 【分析】 ( ) ( )cos( ) ( )x xf x e e x f x−− = − − = − ( )cosx xy e e x−∴ = − 0x xe e−− > cos 0x > ( )cos 0x xe e x−− > ( ) ( )sinf x x θ= + [ ]0,π θ 2 π π 3 2 π - 4 - 依次将选项中的 代入，结合正弦、余弦函数的图象即可得到答案. 【详解】当 时， 在 上不单调，故 A 不正确； 当 时， 在 上单调递减，故 B 不正确； 当 时， 在 上不单调，故 C 不正确； 当 时， 在 上单调递增，故 D 正确. 故选：D 【点睛】本题考查正弦、余弦函数 单调性，涉及到诱导公式的应用，是一道容易题. 7.已知 是定义在 上的奇函数，当 时， ，若 ，则 （ ） A. -1 B. 0 C. -2 D. 1 【答案】C 【解析】 【分析】 根据 是定义在 上的奇函数，可得 ，由 可得 ，求出 ， 即可得出结论. 【详解】因为 是奇函数，所以 ， 可得 .所以当 时， ， 所以 ，又 ，所以 . 故选:C 【点睛】本题考查奇函数的对称性，属于基础题. 8.如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图（每 个受访者都只能在问卷的 5 个活动中选择一个），以下结论错误的是（　　） 的 θ 0θ = ( ) sinf x x= [ ]0,π 2 πθ = ( ) cosf x x= [ ]0,π θ π= ( ) sinf x x= − [ ]0,π 3 2 πθ = ( ) cosf x x= − [ ]0,π ( )f x R 0x > ( ) lnf x a x a= + ( ) 4f e− = (0) (1)f f+ = ( )f x R (0) 0f = ( ) 4f e− = ( ) 4f e = − a ( )f x ( ) ( ) 2 4f e f e a− = − = − = 2a = − 0x > ( ) 2ln 2f x x= − − (1) 2f = − (0) 0f = (0) (1) 2f f+ = − - 5 - A. 回答该问卷的总人数不可能是 100 个 B. 回答该问卷的受访者中，选择“设置分类明确的垃圾桶”的人数最多 C. 回答该问卷的受访者中，选择“学校团委会宣传”的人数最少 D. 回答该问卷的受访者中，选择“公益广告”的人数比选择“学校要求”的少 8 个 【答案】D 【解析】 【分析】 先对图表数据分析处理，再结合简单的合情推理逐一检验即可得解． 【详解】对于选项 A，若回答该问卷的总人数不可能是 100 个，则选择③④⑤的同学人数不 为整数，故 A 正确， 对于选项 B，由统计图可知，选择“设置分类明确的垃圾桶”的人数最多，故 B 正确， 对于选项 C，由统计图可知，选择“学校团委会宣传”的人数最少，故 C 正确， 对于选项 D，由统计图可知，选择“公益广告”的人数比选择“学校要求”的少8%，故 D 错 误， 故选 D． 【点睛】本题考查了对图表数据的分析处理能力及简单的合情推理，属中档题． 9.已知 m，n 表示两条不同的直线，α 表示平面．下列说法正确的是（ ） A. 若 m∥α，n∥α，则 m∥n B. 若 m⊥α，n⊥α，则 m∥n C. 若 m⊥α，m⊥n，则 n∥α D. 若 m∥α，m⊥n，则 n⊥α 【答案】B 【解析】 【分析】 对于 ，直线 与直线 平行、相交、异面都有可能；对于 ，根据直线与平面垂直的性质 定理可知正确；对于 ，可得 n∥α 或 ，对于 ，可得 n⊥α 或 或 或 与 A m n B C n ⊂ α D / /n α n ⊂ α n α - 6 - 相交但不垂直. 【详解】对于 ，若 m∥α，n∥α，则 m∥n 或 与 相交或 与 异面，故 不正确； 对于 ，根据垂直于同一个平面的两条直线平行可知， 正确； 对于 ，若 m⊥α，m⊥n，则 n∥α 或 ，故 不正确； 对于 ，若 m∥α，m⊥n，则 n⊥α 或 或 或 与 相交但不垂直，故 不正确. 故选：B. 【点睛】本题考查了直线与平面垂直的性质定理，考查了空间直线与直线，直线与平面的位 置关系，属于基础题. 10.甲乙丙丁四人中，甲说：我年纪最大，乙说：我年纪最大，丙说：乙年纪最大，丁说：我 不是年纪最大的，若这四人中只有一个人说的是真话，则年纪最大的是（ ） A. 甲 B. 乙 C. 丙 D. 丁 【答案】C 【解析】 【分析】 分别假设甲乙丙丁说的是真话，结合其他人的说法，看是否只有一个说的是真话，即可求得 年纪最大者，即可求得答案. 【详解】①假设甲说的是真话，则年纪最大的是甲，那么乙说谎，丙也说谎，而丁说的是真 话，而已知只有一个人说的是真话，故甲说的不是真话，年纪最大的不是甲； ②假设乙说的是真话，则年纪最大的是乙，那么甲说谎，丙说真话，丁也说真话，而已知只 有一个人说的是真话，故乙说谎，年纪最大的也不是乙； ③假设丙说的是真话，则年纪最大的是乙，所以乙说真话，甲说谎，丁说的是真话，而已知 只有一个人说的是真话，故丙在说谎，年纪最大的也不是乙； ④假设丁说的是真话，则年纪最大的不是丁，而已知只有一个人说的是真话，那么甲也说谎， 说明甲也不是年纪最大的，同时乙也说谎，说明乙也不是年纪最大的，年纪最大的只有一人， 所以只有丙才是年纪最大的，故假设成立，年纪最大的是丙. 综上所述，年纪最大的是丙 故选：C. 【点睛】本题考查合情推理，解题时可从一种情形出发，推理出矛盾的结论，说明这种情形 不会发生，考查了分析能力和推理能力，属于中档题. A m n m n A B B C n ⊂ α C D / /n α n ⊂ α n α D - 7 - 11.已知函数 f(x) sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数，且 y=f(x)图象的两相邻对称 轴间的距离为 ，则 f( )的值为（ ） A. ﹣1 B. 1 C. . D. 【答案】B 【解析】 【分析】 利用辅助角公式进行化简，结合 f(x)是偶函数，求出 φ 的值，利用 f(x)的对称轴之间的距离 求出函数的周期和 ω，代入进行求值即可. 【详解】f(x) sin(ωx+φ)﹣cos(ωx+φ)=2sin(ωx+φ )， ∵f(x)是偶函数，∴φ kπ ，k∈Z， 得 φ=kπ ， ∵0<φ<π，∴当 k=0 时，φ ， 即 f(x)=2sin(ωx )=2sin(ωx )=2cosωx， ∵y=f(x)图象的两相邻对称轴间的距离为 ， ∴ ，即 T=π，即 π， 得 ω=2， 则 f(x)=2cos2x， 则 f( )=2cos(2 )=2cos 1， 故选：B. 【点睛】本题主要考查三角函数值的计算，利用辅助角公式，结合三角函数的性质求出函数 的解析式是解决本题的关键.难度不大. 12.若点 为抛物线 上一点， 是抛物线的焦点， ，点 为直线 上的 动点，则 的最小值为（ ） A. B. C. D. 8 3= 2 π 6 π 3 2 3= 6 π− 6 π− = 2 π+ 2 3 π+ 2 3 π= 2 3 6 π π+ − 2 π+ 2 π 2 2 T π= 2π ω = 6 π 6 π× 123 2 π = × = A 2 4y x= F | 6|AF = P 1x = − | | | |PA PF+ 2 13 2 21 2 14+2 - 8 - 【答案】B 【解析】 【分析】 利用抛物线的定义 ，求得 的坐标，再求得焦点 关于直线 的对称点为 ，然后利用 求解. 【详解】由抛物线的定义得： ， ， 代入 得： ， 不妨设 ， 点 关于直线 的对称点为 ， 故选：B 【点睛】本题主要考查抛物线的几何性质，点关于直线的对称问题以及线段和最小问题，还 考查了运算求解的能力，属于中档题. 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分 13.已知向量 ，若 与 共线，则| |＝_____． 【答案】 【解析】 【分析】 根据题意，由向量平行的坐标表示方法可得 ，即可得 ；由向量模 的计算公式计算可得答案． 【详解】解：根据题意，向量 ， ， 若 与 共线，则有 ，则 ； 则 ； | 1 62 = + = + =A A p|AF x x A F 1x = − ( )3,0E − | | | | | | | |+ = + ≥PA PF PA PE AE | 1 62 = + = + =A A p|AF x x 5Ax = 2 4y x= 2 20=Ay ( )5,2 5A F 1x = − ( )3,0E − ( ) ( )22| | | | | | | | 5 3 2 5 2 21+ = + ≥ = + + =PA PF PA PE AE 11, , ( 2, )2  = − = −   a b m a b b 5 1( ) ( 2) 12m = − × − = ( 2,1)b = − 11, 2a  = −    ( 2, )b m= − a b 1( ) ( 2) 12m = − × − = ( 2,1)b = − | | 4 1 5b = + = - 9 - 故答案为： ． 【点睛】本题考查向量平行的坐标表示，注意向量平行的坐标计算公式即可，属于基础题． 14.甲、乙两人进行乒乓球比赛，比赛规则为“3 局 2 胜”，即先赢 2 局者为胜，根据经验，甲在 每局比赛中获胜的概率为 ，已知第一局甲胜，则本次比赛中甲获胜的概率为_____． 【答案】 【解析】 【分析】 本题利用独立事件概率乘法公式，讨论甲在第几局获胜求解． 【详解】解：依题意，已知第一局甲胜，则比赛中甲获胜有 2 种可能： ①甲在第二局胜； ②甲第二局负，第三局胜； 甲获胜的概率为 ； 故答案为： 【点睛】本题考查了独立事件概率乘法公式，需要讨论甲可能在第几局胜，乙在第几局胜， 需要学生有较强的逻辑分析能力，属于基础题． 15.在△ABC 中，a，b，c 分别是角 A，B，C 的对边，若 b＝1， ，则 S△ABC ＝_____． 【答案】 【解析】 【分析】 首先利用正弦定理可求得 ，利用大边对大角，可求得 ，利用三角形内角和求 得 ，之后利用三角形面积公式求得结果. 【详解】根据正弦定理，有 ，即 ， 5 2 3 8 9 2 2 813 3 3 9 2 + − × =   8 9 23, 3 π= ∠ =c C 3 4 1sin 2B = 6B π= 6A π= sin sin b c B C = 1 3 2sin sin 3 B π= - 10 - 所以有 ，所以 ， 因为 ，所以 ， 所以 ， 所以 S△ABC＝ ， 故答案为： . 【点睛】该题考查的是有关解三角形的问题，涉及到的知识点有正弦定理，三角形内角和求 角，三角形的面积公式，属于基础题目. 16.半正多面体（semiregularsolid）亦称“阿基米德多面体”，是由边数不全相同的正多边形为而 的多面体，体现了数学的对称美．将正方体沿交于一顶点的三条棱的中点截去一个三棱锥， 如此共可截去八个三棱锥，得到一个有十四个面的半正多面体，它们的边长都相等，其中八 个为正三角形，六个为正方形，称这样的半正多面体为二十四等边体．若二十四等边体的棱 长为 ，则该二十四等边体外接球的表面积为_____． 【答案】 【解析】 【分析】 由已知根据该几何体的对称性可知该几何体的外接球即为底面棱长为 ，侧棱长为 2 的正四 棱柱的外接球利用勾股定理得到关于 的方程，进而求解即可. 【详解】由已知根据该几何体的对称性可知该几何体的外接球即为底面棱长为 ，侧棱长为 2 的正四棱柱的外接球， ∴ 1 3 2sin 3 2 B = = 1sin 2B = 1, 3, , (0, )b c b c B π= = < ∈ 6B π= 6A B C ππ= − − = 1 1 1 3sin 1 32 2 2 4bc A = × × × = 3 4 2 8π 2 R 2 2 22 2(2 ) 2 2 2R = + + - 11 - ∴ ， ∴该二十四等边体的外接球的表面积 . 故答案为： 【点睛】本题考查多面体与球的切接问题、球的表面积的求法考查空间想象能力和运算求解 能力求解时注意根据几何体的对称性将问题进行等价转化. 三、解答题：共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17～21 题为 必考题，每个试题考生都必须作答.第 22、23 题为选考题，考生根据要求作答.（一） 必考题：共 60 分 17.已知等差数列{an}的前 n 项和为 Sn，公差 d≠0，a1＝2，且 a1，a2，a4 成等比数列． （Ⅰ）求数列{an}的通项公式及前 n 项和 Sn； （Ⅱ）记 求数列{bn}的前 n 项和 Tn． 【答案】（Ⅰ） ， ；（Ⅱ） 【解析】 【分析】 （Ⅰ）由等比数列的中项性质和等差数列的通项公式，解方程可得公差，进而得到所求通项 公式和求和公式； （Ⅱ）运用数列的分组求和以及数列的裂项相消求和，结合等比数列的求和公式，计算可得 所求和． 【详解】解：（Ⅰ） ， ， 成等比数列， ， ， ，解得 或 （舍去）， ， ． （Ⅱ）由（Ⅰ）得 ， ， 2R = 224 4 2 8S Rπ π π= = × = 8π 12 1 1 n n n b S a − = + 2na n= ( 1)nS n n= + 1 12 1 2nn − −+ 1a 2a 4a ∴ 2 2 1 4a a a=  1 2a = 2(2 ) 2(2 3 )d d∴ + = + 2d = 0d = 2 ( 1) 2 2na n n∴ = + − × = (2 2 ) ( 1)2n n nS n n += = + 1 1 1 1 ( 1) 1nS n n n n = = −+ + 1 1 2 1 1 1 2 2 2n n na − −= =  - 12 - ， ． 【点睛】本题考查等差数列的通项公式和求和公式的运用，等比数列的中项性质，以及数列 的裂项相消求和，考查方程思想和运算能力，属于中档题． 18.如图，在 Rt△AOB 中，OA＝OB＝2，△AOC 通过△AOB 以直线 OA 为轴顺时针旋转 120° 得到（即∠BOC＝120°），点 M 为线段 BC 上一点，且 MB＝ ． （Ⅰ）求证：OA⊥OM； （Ⅱ）若 D 是线段 AB 的中点，求四棱锥 O﹣ACMD 的体积． 【答案】（Ⅰ）证明见解析；（Ⅱ） 【解析】 【分析】 （Ⅰ）由余弦定理得 ，再由勾股定理求出 ，由题意得 ， ，从而 平面 ，即可得到 ． （Ⅱ）由 ， ，能求出四棱锥 的体积． 【详解】解：（Ⅰ）证明：在 中， ， ， 1 1 1 1 2n nb n n = − ++ ∴ 1 1(1 )1 1 1 1 1 2 2(1 ) ( ) ( ) 12 2 3 1 1 2 n nT n n − = − + − +…+ − ++ − 1 1 1 11 1 21 2 1 2n nn n = − + − = − −+ + 4 3 3 4 3 9 2 3 3OM = OM OB⊥ OA OB⊥ OA OC⊥ OA ⊥ COB OA OM⊥ M ODB D OMBV V− −= O ACMD A BOC M OBDV V V− − −= − O ACMD− MOB△ 2OB = 4 3 3BM = 30OBM∠ = ° - 13 - 由余弦定理可得 解得 ， ， ， 由题意得 ， ， ， 平面 ， 平面 平面 ， 平面 ， ， （Ⅱ）解： 是线段 的中点， ， ， 四棱锥 的体积为： ． 【点睛】 本题考查线面垂直的证明，考查四棱锥的体积的求法，考查空间中线线、线面、面面间的位 置关系等基础知识，考查运算能力和推理论证能力，属于中档题． 19.3 月底，我国新冠肺炎疫情得到有效防控，但海外确诊病例却持续暴增，防疫物资供不应 求，某医疗器械厂开足马力，日夜生产防疫所需物品．已知该厂有两条不同生产线 A 和 B 生 产同一种产品各 10 万件，为保证质量，现从各自生产的产品中分别随机抽取 20 件，进行品 质鉴定，鉴定成绩的茎叶图如图所示： 2 2 2 2 cosOM OB BM OB BM OBM= + − ⋅ ⋅ ∠ 2 3 3OM = 2 2 2OM OB MB∴ + = OM OB∴ ⊥ OA OB⊥ OA OC⊥ OB OC O=  OB ⊂ COB OC ⊂ COB OA∴ ⊥ COB OM ⊂ COB OA OM∴ ⊥ D AB 1 1 3 2 32 2 23 2 2 3A BOCV −∴ = × × × × × = 1 1 2 3 2 32 13 2 3 9M ODB D OMBV V− −= = × × × × = ∴ O ACMD− 4 3 9O ACMD A BOC M OBDV V V− − −= − = - 14 - 该产品的质量评价标准规定：鉴定成绩达到[90，100）的产品，质量等级为优秀；鉴定成绩达 到[80，90）的产品，质量等级为良好；鉴定成绩达到[60，80）的产品，质量等级为合格．将 这组数据的频率视为整批产品的概率． （Ⅰ）从等级为优秀的样本中随机抽取两件，求抽取的两件产品中至少有一件是 A 生产线生 产的概率； （Ⅱ）请完成下面列联表，并判断能否在误差不超过 0.05 的情况下认为产品等级是否达到良 好及以上与生产产品的生产线有关？ A 生产线生产的产品 B 生产线生产的产品 合计 良好及以上 合格 合计 附：K2＝ ，其中 n＝a+b+c+d． P（K2≥k0） 010 0.05 0.01 0.005 k0 2.706 3.841 6.635 7.879 【答案】（Ⅰ）0.7；（Ⅱ）表格见解析，误差不超过0.05 的情况下，不能认为产品等级是否 达到良好以上与生产产品的生产线有关 【解析】 【分析】 （Ⅰ）从图中可知样本中优秀的产品有 2 件来自 生产线，3 件来自 生产线，根据古典概型 2( ) ( )( )( )( ) − + + + + n ad bc a b c d a d b c A B - 15 - 概率公式计算即可得抽取的两件产品中至少有一件是 A 生产线生产的概率． （Ⅱ）完成 2×2 列联表，求出 观测值，对比临界值表，即可得出结论. 【详解】（Ⅰ）从图中可知样本中优秀的产品有 2 件来自 生产线，3 件来自 生产线， 设 为来自 机器生产的产品数量，至少有一件是 A 生产线生产的概率为 ， ， ， ∴ . (2)由已知得 2×2 列联表为： A 生产线生产的产品 B 生产线生产的产品 合计 良好及以上 6 12 18 合格 14 8 22 合计 20 20 40 ∴ ∴在误差不超过 0.05 的情况下，不能认为产品等级是否达到良好以上与生产产品的生产线有 关. 【点睛】本题考查独立性检验，考查古典概型概率的计算，考查学生分析问题的能力和计算 能力，属于基础题. 20.已知椭圆 过点 E（ ，1），其左、右顶点分别为 A、B，且 离心率 ． 求椭圆 C 的标准方程； （Ⅱ）设 M（x0，y0）为椭圆 C 上异于 A，B 两点的任意一点，直线 l：x0x+2y0y﹣4＝0．证明： 2K A B X A P 2 2 2 5 ( 2) 0.1CP X C = = = 1 1 2 3 2 5 ( 1) 0.6= = =C CP X C ( 1) ( 2) 0.1 0.6 0.7PP X P X= + = + == = 2 2 2 ( ) 40 (12 14 6 8) 40 3.636 3.841( )( )( )( ) 20 20 18 22 11 n ad bcK a b c d a c b d − × × − ×= = = ≈ <+ + + + × × × 2 2 2 2: 1 ( 0)x yC a ba b + = > > 2 2 2e = - 16 - 直线 l 与椭圆 C 有且只有一个公共点． 【答案】（Ⅰ） ;（Ⅱ）见解析. 【解析】 【分析】 （Ⅰ）根据题意，列出关于 的方程组，解出 的值，即可求出椭圆 的方程； （Ⅱ）联立直线 与椭圆方程，结合 在椭圆上， ，可求出唯一交点坐 标 ，即直线 与椭圆 有且只有一个公共点，即点 ． 【详解】（Ⅰ）由题意可知, ,解得 ， ∴椭圆 C 的方程为： ； （Ⅱ）由题意知 ， 联立方程 ,消去 得： ， ∵ 在椭圆上,∴ ， ∴ ,即 ， ∴ ， ∴直线 与椭圆 有且只有一个公共点，即点 . 【点睛】本题考查椭圆的标准方程，考查直线与椭圆的综合，考查计算能力和推理能力，属 于中档题. 21.已知函数 ． （1）讨论函数 的单调性： 2 2 14 2 x y+ = a b c， ， a b c， ， C l ( )0 0,M x y 2 2 0 02 4x y+ = ( )0 0,x y l C M 2 2 2 2 2 2 1 1 2 2 a b c a a b c  + =   =  = +  2 2 2 a b c =  =  = 2 2 14 2 x y+ = 0 0y ≠ 2 2 0 0 14 2 2 4 0 x y x x y y  + =  + − = y ( )2 2 2 2 0 0 0 02 8 16 8 0x y x x x y+ − + − = ( )0 0,M x y 2 2 0 02 4x y+ = 2 2 0 02 0x x x x− + = ( )2 0 0x x− = 0 0,x x y y= = l C M 21( ) ( 1) ( 2) ( 0)2 xf x a x x e a= − − + − > ( )f x - 17 - （2）若关于 的方程 存在 3 个不相等的实数根，求实数 的取值范围． 【答案】（1）答案见解析；（2） 或 ． 【解析】 【分析】 （1）先对函数求导，然后结合导数与单调性的关系对 进行分类讨论即可求解； （2）转化为相应的函数的交点问题，结合导数研究函数的特征，然后结合图象可求． 【详解】解：（1） ， ，由 可得 或 ， 当 时， ， 在 ， 上， ， 单调递增，在 上， ， 单调递 减； 当 时， ， 在 上恒成立，即 在 上单调递增； 当 时， ， 在 ， 上， ， 单调递增，在 上， ， 单调递 减； （2） 有 3 个实数根， 显然是方程的一个解，故 有 2 个实数根且 ， ， 即 ， 令 ，则 ， 当 ， 时， ， 单调递减，当 ， ， ， 单调递增， 当 时， ， 时， 取得极小值， ， 又 ，则 或 ． x 1( ) 02f x a+ = a 22e a e< < 2a e> a ( ) ( 1) ( 1) ( 1)( )x xf x a x x e x e a′ = − − + − = − − 0a > ( ) 0f x′ = 1x = x lna= ( )i 0 a e< < 1 lna> (1, )+∞ ( , )lna−∞ ( ) 0f x′ > ( )f x ( ,1)lna ( ) 0f x′ < ( )f x ( )ii a e= 1lne = ( ) 0f x′ > R ( )f x R ( )iii a e> 1lna > ( , )lna +∞ ( ,1)−∞ ( ) 0f x′ > ( )f x (1, )lna ( ) 0f x′ < ( )f x 21 1 1( ) ( 2) ( 2)( ) 02 2 2 x xf x a ax ax x e x e ax+ = − + + − = − − = 2x = 1 02 xe ax− = 0x ≠ 2x ≠ 2 ( 2) xea xx = ≠ 2( ) ( 2) xeg x xx = ≠ 2 2 ( 1)( ) xe xg x x −′ = ( , 0)x ∈ −∞ (0,1) ( ) 0g x′ < ( )g x (1,2)∈ (2, )+∞ ( ) 0g x′ > ( )g x 0x < ( ) 0 - 18 - 【点睛】本题主要考查利用导数求解函数的单调区间及函数零点的求解，体现了转化思想及 数形结合思想的应用，属于中档题． （二）选考题：共 10 分考生从 22、23 题中任选一题作答，如果多做，则按所做 的第一题计分. [选修 4-4：坐标系与参数方程] 22.在直角坐标系 中，直线 的参数方程为 为参数），曲线 的参数方程 为 ， ， 为参数），以坐标原点为极点， 轴的正半轴为极轴建 立极坐标系，且曲线 的极坐标方程为 ． （1）求 ， ， 的值； （2）已知点 的直角坐标为 ， 与曲线 交于 ， 两点，求 ． 【答案】（1） ；（2） 【解析】 【分析】 （1）直接利用转换关系式的应用，把参数方程极坐标方程和直角坐标方程之间转换求出结 果． xOy l 2 2 ( 21 2 x t t y t  = −  = + C cos ( 0sin x m my a n α α = > = + 0n > α x C 8sinρ θ= a m n P (0,1) l C A B | | | |PA PB+ 4a m n= = = 46 - 19 - （2）将直线 的参数方程为 为参数），代入 ，利用一元二次 方程根和系数关系式的应用求出结果． 【详解】解：（1）曲线 的极坐标方程为 ．转换为 ， 则 ， 即 ． 可得参数方程为 ， 又因为曲线 的参数方程为 ， ， 为参数） 所以 ． （2）将直线 的参数方程为 为参数）， 代入 ， 得 ． 设 ， 两点对应的参数分别为 ， ， 则 ， ． 所以 ． 【点睛】本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，一元二次 方程根和系数关系式的应用，主要考查学生的运算能力和转换能力及思维能力，属于中档 题． [选修 4-5：不等式选讲] 23.已知函数 的最小值为 2． （Ⅰ）求不等式 的解集； l 2 2 ( 21 2 x t t y t  = −  = + 2 2( 4) 16x y+ − = C 8sinρ θ= 2 8 sinρ ρ θ= 2 2 8x y y+ = 2 2( 4) 16x y+ − = 4cos 4 4sin x y α α =  = + C cos ( 0sin x m my a n α α = > = + 0n > α 4a m n= = = l 2 2 ( 21 2 x t t y t  = −  = + 2 2( 4) 16x y+ − = 2 3 2 7 0t t− − = A B 1t 2t 1 2 3 2 0t t+ = > 1 2 7 0t t = − < 1 2 1 2 1 2| | | | | | ( ) 4 46PA PB t t t t t t+ = − = + − = ( ) | 2 | | | ( 0)f x x x t t= − + − > ( ) | 4 | 8f x x+ −  - 20 - （Ⅱ）若 ，求 的最大值． 【答案】（Ⅰ） 或 ；（Ⅱ）5 【解析】 分析】 （Ⅰ）先利用绝对值三角不等式求出 的最小值，然后求出 的值，再利用零点分段法解不 等式 即可； （Ⅱ）根据（Ⅰ）可得 ，然后利用基本不等式求出 的最大 值． 【详解】解：（Ⅰ） ， 舍去）， ， 当 时，令 ，得 ， ； 当 时，令 ，得 ，无解； 当 时，令 ，得 ， ． 不等式的解集为 或 ． （Ⅱ）由（Ⅰ）知 ，所以 ， ， ，当且仅当 时等号成立， 的最大值为 5． 【点睛】本题考查了绝对值三角不等式，绝对值不等式的解法和利用基本不等式求最值，考 查了分类讨论思想和转化思想，属于中档题． 【 2 2 2 52 3 5 2a b c t+ + = 2 3ac bc+ 2{ | 3x x 6}x ( )f x t ( ) | 4 | 8f x x+ −  2 2 22 3 5 2 10a b c t+ + = = 2 3ac bc+ | 2 | | | | ( 2) ( ) | | 2 | 2x x t x x t t− + − − − − = − =  4( 0t t∴ = = 10 3 , 2 ( ) 2 2 4 6 ,2 4 3 10, 4 x x f x x t x x x x x x − < ∴ + − = − + − = −  − >   2x < 10 3 8x−  2 3x ∴ 2 3x 2 4x  6 8x−  2x − 4x > 3 10 8x −  6x 6x∴  ∴ 2{ | 3x x 6}x 4t = 2 2 22 3 5 2 10a b c t+ + = = 2 2 2 2 2 2 210 2 3 5 2( ) 3( ) 4 6a b c a c b c ac bc∴ = + + = + + + + 2 3 5ac bc∴ +  1a b c= = = ± 2 3ac bc∴ +