- 528.50 KB
- 2021-04-17 发布
鄂尔多斯市第一中学2016—2017学年度第二学期第二次月考试卷
高三数学试题(文)
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知为虚数单位,则( )
A. B. C. D.
2.已知集合,,则( )
A. B. C. D.
3.已知命题,则( )
A.命题为假命题 B.命题为真命题
C.命题为假命题 D. 命题为真命题
4.设变量,满足约束条件,则目标函数的最大值为( )
A. B. C. D.
5.执行如图所示的程序框图,输出的( )
A. B. C. D.
6.已知是等差数列,且,则( )
A. B. C. D.
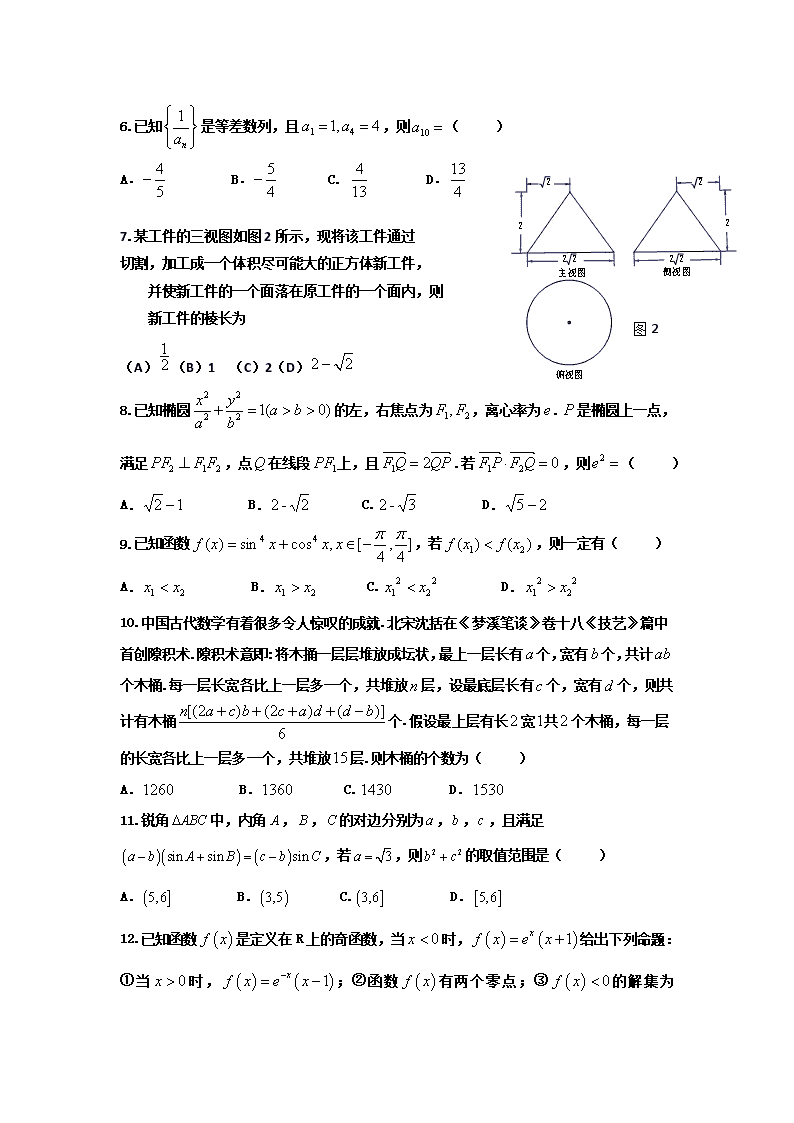
7.某工件的三视图如图2所示,现将该工件通过
切割,加工成一个体积尽可能大的正方体新工件,
并使新工件的一个面落在原工件的一个面内,则
新工件图2
的棱长为
(A)(B)1 (C)2(D)
8.已知椭圆的左,右焦点为,离心率为.是椭圆上一点,满足,点在线段上,且.若,则( )
A. B. C. D.
9.已知函数,若,则一定有( )
A. B. C. D.
10.中国古代数学有着很多令人惊叹的成就.北宋沈括在《梦溪笔谈》卷十八《技艺》篇中首创隙积术.隙积术意即:将木捅一层层堆放成坛状,最上一层长有个,宽有个,共计个木桶.每一层长宽各比上一层多一个,共堆放层,设最底层长有个,宽有个,则共计有木桶个.假设最上层有长宽共个木桶,每一层的长宽各比上一层多一个,共堆放层.则木桶的个数为( )
A. B. C. D.
11.锐角中,内角,,的对边分别为,,,且满足,若,则的取值范围是( )
A. B. C. D.
12.已知函数是定义在R上的奇函数,当时,给出下列命题:①当时,;②函数有两个零点;③的解集为
;④,都有。其中正确的命题个数为
A. 4 B. 3 C. 2 D. 1
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知双曲线的离心率为,则该双曲线的渐近线方程为
14.已知向量,,且,则的模等于.
15.四棱锥的底面是边长为6的正方形,且,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是.
16.已知数列满足,,数列为等差数列,且,,则.
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知:复数,,且,其中A、B、C为△ABC的内角,、、为角、、所对的边.
(Ⅰ)求角的大小;
(Ⅱ) 若,求△ABC的面积.
18.中央电视台为了解一档诗歌类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
其中一个数字被污损
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率;
(2)随着节目的播出,极大激发了观众对诗歌知识的学习积累热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习诗歌知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
由表中数据,试求线性回归方程,并预测年龄在60岁的观众周均学习诗歌知识的时间.
19. 如图,平面五边形中,∥,且,.将沿折起,使点到的位置,且,得到四棱锥.
(1)求证:平面;
(2)记平面与平面相交于直线,求证:∥.
21.设两点在抛物线上,是AB的垂直平分线,
(Ⅰ)当且仅当取何值时,直线经过抛物线的焦点F?证明你的结论;
(Ⅱ)若,弦AB是否过定点,若过定点,求出该定点,若不过定点,说明理由.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点为极点,轴的非负半轴为极轴建立极坐标系,圆的极坐标方程为.
(1)求出圆的直角坐标方程;
(2)已知圆与轴相交于,两点,直线:关于点对称的直线为.若直线上存在点使得,求实数的最大值.
23.选修4-5:不等式选讲
已知函数.
(1)求函数的定义域;
(2)若当时,不等式恒成立,求实数的取值范围.
数学试题(文)参考答案
一、选择题
1-5:DADCC 6-10:ABCDB 11、12:AB
二、填空题
13. 14.1 15. 16.225
三、解答题
(17)解:(Ⅰ)∵
∴----①,----② ----------------------------2分
由①得
即----------③ -------------------------------4分
∴,∵ ∴-------------------------------------------------------------6分
(Ⅱ) ∵,由余弦定理得
,--④-------------------------------------------------------------------------------8分
由②得------------⑤
由④⑤得, -------------------------------------------------------------------------------------10分
∴=.--------------------------------------------------12分
18.(1)
19.解:(1)在中,∵,,由余弦定理得.
连接,∵.
又∵,∴在中,,即.
同理,,平面,,故平面.
(2)∵∥,且平面,平面,
∴∥平面,又平面平面,∴∥.
20.
21.解:(Ⅰ)∵抛物线,即,
∴焦点为………………………………………………………1分
(1)直线的斜率不存在时,显然有………………………………3分
(2)直线的斜率存在时,设为k, 截距为b
即直线:y=kx+b 由已知得:
……………5分
……………7分
即的斜率存在时,不可能经过焦点……………………………………8分
所以当且仅当=0时,直线经过抛物线的焦点F…………………………9分
(Ⅱ)过定点(0,)
22.解:(1)由得,即,即圆的标准方程为.
(2):关于点的对称直线的方程为,而为圆的直径,故直线上存在点使得的充要条件是直线与圆有公共点,故,于是,实数的最大值为.
23.解:(1),
当时,函数的定义域为;当时,函数的定义域为.
(2),记,因为,所以需且只需,又,所以,,且.