2020届湖南省衡阳市第八中学高三上学期第六次月考数学（理）试题（解析版） 23页

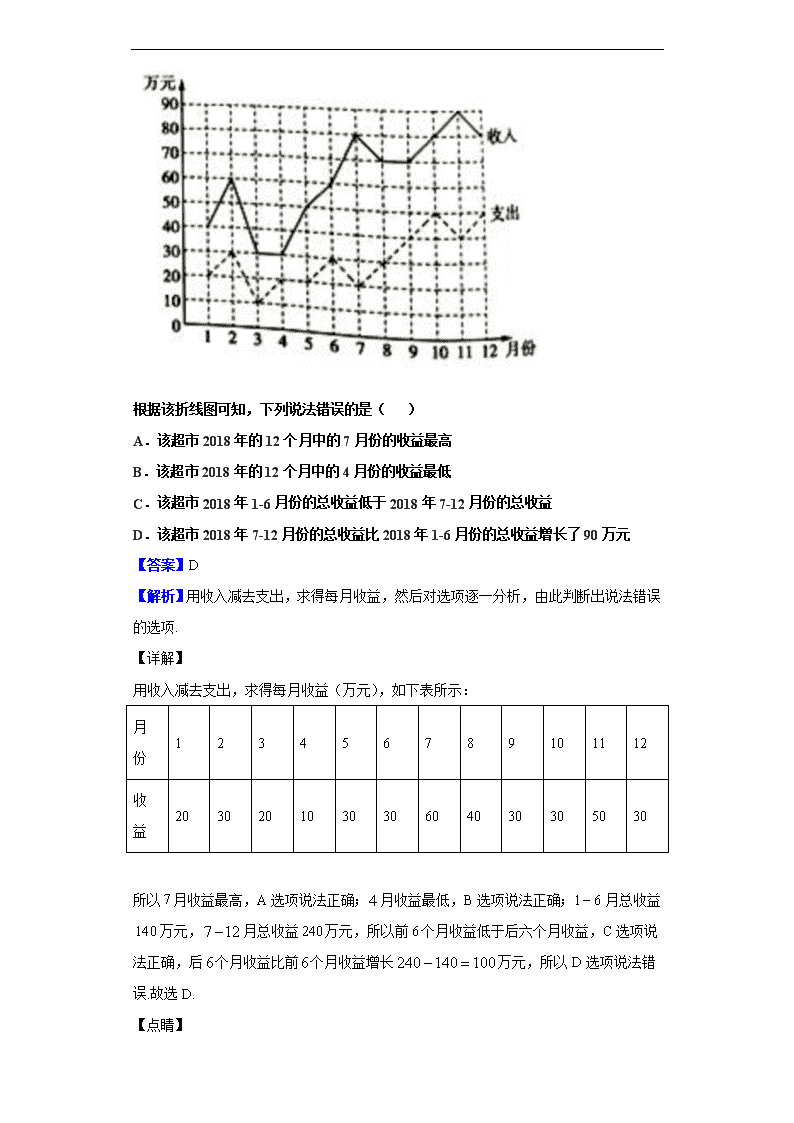
2020 届湖南省衡阳市第八中学高三上学期第六次月考数学 （理）试题 一、单选题 1．设集合 ， ，则 （ ） A． B． C． D． 【答案】B 【解析】A={x|y=log2（2﹣x）}={x|x＜2}， B={x|x2﹣3x+2＜0}={x|1＜x＜2}， 则∁AB={x|x≤1}， 故选 B． 2．设 为虚数单位，若 是纯虚数，则 （ ） A． B． C．1 D． 【答案】A 【解析】按照复数的代数形式的乘除运算，计算复数 ，再根据复数 是纯虚数即实部 为零，得到方程解得. 【详解】 解： 又因为复数 是纯虚数 解得 故选： 【点睛】 本题考查复数代数形式的乘除运算以及复数的相关概念，属于基础题. 3．已知某超市 2018 年 12 个月的收入与支出数据的折线图如图所示： ( )2{ | log 2 }A x y x= = − 2{ | 3 2 0}B x x x= − + < AC B= ( ),1−∞ ( ],1−∞ ( )2,+∞ [ )2,+∞ i ( )2 a iz a Ri −= ∈+ a = 1 2 1 2 − 1− z z ( )( ) ( )( ) ( ) ( )2 2 1 2 2 1 2 2 2 2 5 5 5 a i i a a ia i a az ii i i − − − + − −− − − −= = = = ++ + − z 2 1 05 a −∴ = 1 2a = A 根据该折线图可知，下列说法错误的是（ ） A．该超市 2018 年的 12 个月中的 7 月份的收益最高 B．该超市 2018 年的 12 个月中的 4 月份的收益最低 C．该超市 2018 年 1-6 月份的总收益低于 2018 年 7-12 月份的总收益 D．该超市 2018 年 7-12 月份的总收益比 2018 年 1-6 月份的总收益增长了 90 万元 【答案】D 【解析】用收入减去支出，求得每月收益，然后对选项逐一分析，由此判断出说法错误 的选项. 【详解】 用收入减去支出，求得每月收益（万元），如下表所示： 月 份 1 2 3 4 5 6 7 8 9 10 11 12 收 益 20 30 20 10 30 30 60 40 30 30 50 30 所以 月收益最高，A 选项说法正确； 月收益最低，B 选项说法正确； 月总收益 万元， 月总收益 万元，所以前 个月收益低于后六个月收益，C 选项说 法正确，后 个月收益比前 个月收益增长 万元，所以 D 选项说法错 误.故选 D. 【点睛】 7 4 1 6− 140 7 12− 240 6 6 6 240 140 100− = 本小题主要考查图表分析，考查收益的计算方法，属于基础题. 4．已知 ，则 （ ） A． B． C． D． 【答案】D 【解析】利用诱导公式及二倍角公式将 变形为 ， 再代入求值即可. 【详解】 解： 故选： 5．已知 ， 满足 ，则（　　） A． B． C． D． 【答案】A 【解析】根据对数的化简公式得到 ,由指数的运算公式得到 = ，由对数的性质得到 >0, ，进而得到结果. 3sin( )3 2 2 π α− = − 2020cos( )3 π α+ = 3 2 3 2 − 1 2 1 2 − 2020cos 3 π α +   21 2sin 3 2 π α − −   2020cos cos 673 cos cos 23 3 3 3 2 π π π π αα π α α π        + = + + = − + = − − −                 cos2 3 2 π α = −   21 2sin 3 2 π α = − −   3sin( )3 2 2 π α− = − 2 2 3 11 2sin 1 23 2 2 2 π α   ∴ − − = − − = −        2020 1cos 3 2 π α ∴ + = −   D 1 2 1 2 1ln ,2x x e −= = 3x 3 3lnxe x− = 1 2 3x x x< < 1 3 2x x x< < 2 1 3x x x< < 3 1 2x x x< < 1 1ln 2 02x ln= = − < 1 2 2x e −= ( )1 0,1 e ∈ 3 3lnxe x− = 3 1x∴ > 【详解】 已知 , = , >0, 进而得到 . 故答案为 A. 【点睛】 本题考查了指对函数的运算公式和对数函数的性质；比较大小常用的方法有：两式做差 和 0 比较，分式注意同分，进行因式分解为两式相乘的形式；或者利用不等式求得最值， 判断最值和 0 的关系. 6．函数 图象的大致形状是（　　） A． B． C． D． 【答案】C 【解析】化简函数，确定函数奇偶性，讨论函数在 内正负情况，即可排除所有错 误选项. 【详解】 则 ，是偶函数，排除 B、D. 当 时， 即 ，排除 A. 故选:C. 【点睛】 解复杂函数的图像问题，一般采取排除法.利用单调性，奇偶性，极值，以及函数值的 正负进行判断. 1 1ln 2 02x ln= = − < 1 2 2x e −= ( )1 0,1 e ∈ 3 3lnxe x− = 3 1x∴ > 1 2 3x x x< < 2( ) 1 sin1 xf x xe  = − +  (0, )2 π 2 1( ) ( 1)sin sin1 1 x x x ef x x xe e −= − =+ + 1 1 1( ) sin( ) ( sin ) sin ( )1 1 1 x x x x x x e e ef x x x x f xe e e − − − − −− = − = ⋅ − = =+ + + (0, )2x π∈ 1,sin 0xe x> > ( ) 0f x < 7．公元前 5 世纪，古希腊哲学家芝诺发表了著名的阿基里斯悖论：他提出让乌龟在阿 基里斯前面 1000 米处开始，和阿基里斯赛跑，并且假定阿基里斯的速度是乌龟的 10 倍. 当比赛开始后，若阿基里斯跑了 1000 米，此时乌龟便领先他 100 米；当阿基里斯跑完 下一个 100 米时，乌龟仍然前于他 10 米.当阿基里斯跑完下一个 10 米时，乌龟仍然前 于他 1 米……，所以，阿基里斯永远追不上乌龟.根据这样的规律，若阿基里斯和乌龟 的距离恰好为 米时，乌龟爬行的总距离为（ ） A． B． C． D． 【答案】B 【解析】根据条件，乌龟每次爬行的距离构成等比数列，公比为 当阿基里斯和乌龟的速度恰好为 米时，乌龟爬行的总距离为 故选 8．函数 ， ， ，且 在 上单调，则下列说法正确的是( ) A． B． C．函数 在 上单调递增 D．函数 的图象关于点 对称 【答案】C 【解析】由题意得函数 的最小正周期为 ， ∵ 在 上单调， ∴ ，解得 ． ∵ ， ， 210− 410 1 90 − 510 1 900 − 510 9 90 − 410 9 900 − 1 10 210− 55 2 1100 1 10 110100 10 ... 10 1 9001 10 −  −  − + + + = = − B ( ) ( )( )2sin 0,0f x xω ϕ ω ϕ π= + > < < 28f π  =   02f   =   π ( )f x ( )0,π 1 2 ω = 6 2 8 2f π − − =   ( )f x , 2 ππ − −   ( )y f x= 3 ,04 π     ( )f x 2T π ω= ( )f x ( )0,π 2 T π πω= ≥ 0 1ω< ≤ 28f π  =   02f π  =   ∴ ，解得 ， ∴ ． 对于选项 A，显然不正确． 对于选项 B， ，故 B 不正确． 对于选项 C，当 时， ，所以函数 单调递增，故 C 正确． 对于选项 D， ，所以点 不是函数 图象的对称中心，故 D 不正确． 综上选 C． 点睛：解决函数 综合性问题的注意点 （1）结合条件确定参数 的值，进而得到函数的解析式． （2）解题时要将 看作一个整体，利用整体代换的方法，并结合正弦函数的相关 性质求解． （3）解题时要注意函数图象的运用，使解题过程直观形象化． 9． 中， ，满足 ，则 的面积的最大值为 （ ） A． B．2 C． D． 【答案】A 【解析】利用数量积公式以及平方关系计算得到 ，利用模长公式以及基本不 等式得到 ，结合三角形面积公式化简即可求解. 【详解】 ,即 3 8 4 2 ωπ πϕ ωπ ϕ π  + =  + = 2 3 2 3 ω πϕ  =  = 2 2( ) 2sin 3 3f x x π = +   2 2 7 6 2( ) 2sin 2sin8 3 8 3 12 2f π π π π + − = − × + = =   2x ππ− ≤ ≤ − 2 20 3 3 3x π π≤ + ≤ ( )f x 3 2 3 2 7( ) 2sin 2sin 04 3 4 3 6f π π π π = × + = ≠   3 ,04 π     ( )f x ( )( ) sinf x A xω ϕ= + , ,A ω ϕ xω ϕ+ AOB OA a OB b= =   ， | | 2a b a b⋅ = − =    AOB∆ 3 2 3 2 2 sin AOB∠ | || | 4a b ≤ | || | cos 2a b a b AOB⋅ = ∠ =   2cos | || | AOB a b ∠ =  ，即 所以 所以 故选：A 【点睛】 本题主要考查了平面向量的数量积公式以及模长公式的应用，属于中档题. 10．已知双曲线 ： （ ， ）， ， 分别为其左、右焦点， 为坐标原点，若点 关于渐近线的对称点恰好落在以 为圆心， 为半径的圆上， 则双曲线 的离心率是（ ） A． B． C． D． 【答案】C 【解析】 由题意， ， ，设一条渐近线方程为 ，则 到渐近线的距离为 ，设 关于渐近线的对称点为 ， 与渐近线交于 ，则 ， ， 为 的中点，又 是 的中点， ， 为直角， 为直角三角形， 由勾股定理得 ， ， ， ，则 . 22 (| || |) 4 sin 1 | || 2 | | || | a b AOB a b a b − ∴ ∠ = − =        2 2| | | | 2 | | 2a b a a b b− = − ⋅ + =     2 28 | | | | 2 | || |a b a b= + ≥   | || | 4a b ≤ 2 2(| || |) 41 1 1 1| || | sin | || | = (| || |) 4 16 4= 32 2 2 2| || |AOB a bS a b AOB a b a b a b∆ −= ∠ = − ≤ −      C 2 2 2 2 1x y a b − = 0a > 0b > 1F 2F O 2F 1F 1OF C 2 3 2 3 1( ,0)F c− 2 ( ,0)F c by xa = 2F b 2F M 2F M A 1MF c= 2 2MF b= A 2MF O 1 2F F 1/ /OA F M 1 2F MF∴∠ 1 2MF F∴ ∴ 2 2 24 4c c b= + ( )2 2 23 4c c a∴ = − 2 24c a∴ = 2c a∴ = 2e = 故选：C 点睛：解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于 a，b，c 的方程或不等式，再根据 a，b，c 的关系消掉 b 得到 a，c 的关系式，建立关于 a，b，c 的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等. 11．在正方体 中， ， 分别为 ， 上的动点，且满足 ，则下列 4 个命题中，所有正确命题的序号是（ ）． ①存在 ， 的某一位置，使 ② 的面积为定值 ③当 时，直线 与直线 一定异面 ④无论 ， 运动到何位置，均有 A．①②④ B．①③ C．②④ D．①③④ 【答案】D 【解析】依次判断，每个选项：①当 ， 分别为棱 ， 的中点时满足，正确； 取特殊位置 的面积为变化，故错误；③假设不成立推出矛盾，正确；④ 平面 ，正确.得到答案. 【详解】 ①当 ， 分别为棱 ， 的中点时满足，正确； ②当 与 重合时： ；当 与 重合时： （ 为正方体 边长），错误； ③当 时，假设直线 与直线 是共面直线，则 与 共面，矛盾，正 确； ④如图所示： 分别为 在平面内的投影，易证 平面 ，正确. 故选： 1 1 1 1ABCD A B C D− P Q 1AD 1B C 1AP B Q= P Q AB PQ∥ BPQ 0PA > 1PB AQ P Q BC PQ⊥ P Q 1AD 1B C BPQ BC ⊥ PFGQ P Q 1AD 1B C P A 21 2BPQS a=  P 1D 22 2BPQS a=  a 0PA > 1PB AQ AP 1B Q ,F G ,P Q BC ⊥ PFGQ D 【点睛】 本题考查了空间几何中直线的平行，垂直，异面，意在考查学生的空间想象能力. 12．若函数 在区间 内有两个不同的零点，则 实数 的取值范围是（ ） A． B． C． D． 【答案】D 【解析】分离常数，构造函数，利用导数求出函数的最值，即可求出实数 的取值. 【详解】 解： 在 内有两解， 令 则 在 为减函数，在 上为增函数， 当 时，取得最小值 且当 时， ， 1 2( ) 2 log ( 0)x xf x e x a a−= + − > (0, 2) a 2( 2, 2 ) e (0, 2] 2 2( 2, 2 ) e+ 3 4 2 4(2 , 2 ) e+ a ( ) 1 22 log 0x xf x e x a−= + − = 1 2log 12 xea x − ∴ = + ( )0,2 ( ) 1 12 xef x x − = + ( ) ( )1 2 1 2 xe xf x x − −′ = ( )f x∴ ( )0,1 ( )1,2 ∴ 1x = ( ) ( ) 1 1 min 31 12 1 2 ef x f − = = + =× 0x → ( )f x → +∞ ( ) 2 1 42 12 2 4 e ef − += + =× 2 3 4log2 4 ea +∴ < < 故选： 【点睛】 本题考查函数的零点问题，参变分离是解答的关键，属于中档题. 二、填空题 13．若 ax2+ 的展开式中 x5 的系数是—80，则实数 a=_______. 【答案】-2 【解析】试题分析：因为 ，所以由 ， 因此 【考点】二项式定理 【名师点睛】本题是二项式定理问题中的常见题型，二项展开式的通项往往是考查的重 点.本题难度不大，易于得分.能较好地考查考生的基本运算能力等. 14．在菱形 中， ，将这个菱形沿对角线 折起，使得平面 平面 ，若此时三棱锥 的外接球的表面积为 ，则 的长为_________． 【答案】 . 【解析】建立空间直角坐标系，列出等式求解即可． 【详解】 解：取 中点 ，如图，以 为原点建立空间直角坐标系 ，设 ， 3 4 2 42 2 e a + ∴ < < D ABCD 060DAB∠ = BD DAB ⊥ BDC A BCD− 5π AB 3 BD O O O xyz− 2AB m= 等边三角形 中心为 ，等边三角形 中心为 ，外接球球心为 ， 则 ， ， ， ， ， ， ， 则半径为 ， 因为外接球表面积为 ， 则 ，所以 ，所以 ， 故选： ． 【点睛】 本题考查三棱锥外接球的体积计算方法，属于中档题． 15．已知数列 满足 ， ， ，则(1) ________， (2) _____________. 【答案】 . . 【解析】（1）将已知等式中的 换为 ，作差即求得； （2）将所求式子，整理后，运用等差数列的定义和求和公式，计算可得所求和． 【详解】 解：（1） ， ①， 当 时， 可得 ， ②， ① ②得 ， ； 为以 为首项， 的等差数列， （2） 由（1）得 为公差为 3 的等差数列，又由 可得 ， ABD 1I BCD 2I I (0,0, 3 )A m ( .0,0)B m ( ,0,0)D m− (0, 3 ,0)C m 1 3(0,0, )3I m 2 3(0, ,0)3I m 3 3(0, , )3 3I m m 5 3 R IA m= = 24 5S Rπ π= = 5 5 23 m = 3 2m = 2 3AB m= = B { }na 1 1a = 1 3 5n na a n++ = + *n N∈ 2 1na − = 2 1 1 1( 1) i i n i i aa+ = +− =∑ 3 2n − 29 33 2 2 n n− − n 1n − 1 1a = 1 3 5n na a n++ = + 1n = 2 7a = 1 3 2n na a n− + = + 2n − 1 1 3n na a+ −− = 2n { }2 1na −∴ 1 1a = 3d = 2 1 3 2na n− = −∴ 1 2 2 3 3 4 4 5 2 1 2 2 2 1n n n na a a a a a a a a a a a− +− + − +… − 2 1 3 4 3 5 2 2 1 2 1 2 4 2( ) ( ) ( ) ( 3)( )n n n na a a a a a a a a a a a− += − + − +…+ − = − + +…+ 2{ }na 1 2 8a a+ = 2 7a = 则 ． 故答案为： ； 【点睛】 本题考查等差数列的定义和通项公式、求和公式的运用，考查化简整理的运算能力，属 于中档题． 16．如图，哈尔滨市有相交于点 的一条东西走向的公路 与一条南北走向的公路 ， 有一商城 的部分边界是椭圆的四分之一，这两条公路为椭圆的对称轴，椭圆的长半 轴长为 2，短半轴长为 1(单位:千米). 根据市民建议，欲新建一条公路 ，点 分 别在公路 上，且要求 与椭圆形商城 相切，当公路 长最短时， 的长为 ________千米. 【答案】 【解析】设 为 ,联立 可得 , 利用 可得 ,则 ,利用均值不等式求 最值,再由取等条件求得 即可 【详解】 由题,设 为 ,由图易得 ,联立 可得 ,则 , 即 , 2 1 2 2 3 3 4 4 5 2 1 2 2 2 1 ( 1) 9 33( 3)(7 3)2 2n n n n n n n na a a a a a a a a a a a n− + − +− + − +…+ − = − + = − 3 2n − 29 33 2 n n+− O l m A PQ ,P Q ,l m PQ A PQ OQ 3 PQ y kx b= + 2 2 14 y kx b x y = + + = ( )2 2 21 2 1 04 k x kbx b + + + − =   0∆ = ( )2 21 14k b= − ( ) 2 2 2 2 2 2 21 14 b bPQ b bk b = + = + − OQ PQ y kx b= + 1, 2bb k > − > 2 2 14 y kx b x y = + + = ( )2 2 21 2 1 04 k x kbx b + + + − =   ( ) ( )2 2 212 4 1 04kb k b ∆ = − + − =   ( )2 21 14k b= − 因为 为 , 为 , 则 ,当且仅当 ,即 时取等,即 故答案为： 【点睛】 本题考查圆锥曲线的实际应用,考查利用均值不等式求最值,考查运算能力 三、解答题 17．已知△ABC 的内角 A，B，C 的对边分别为 a，b，c，且 ． （1）求角 B 的值； （2）若△ABC 的面积为 ，设 D 为边 AC 的中点，求线段 BD 长的最小值． 【答案】（1） ；（2） . 【解析】（1）根据 ，化简可得 ，进一步得到 ，然后求出 的值； （2）由（1）的角 及三角形面积公式可得 的值，因为 D 为边 AC 的中点，所以 ，利用向量的模和基本不等式可求 的取值范围，即可得到 的最小值. 【详解】 解：（1）由 ，得 ， P ,0b k  −   Q ( )0,b ( ) 2 2 2 2 2 2 2 2 2 2 2 2 4 441 1 114 b b bPQ b b b bk b bb = + = + = + = + +− −− ( ) ( )2 2 2 2 4 45 1 5 2 1 91 1b bb b = + + − ≥ + ⋅ − =− − 2 2 41 1b b − = − 3b = 3OQ = 3 tan ( sin 2 cos ) cos2 2 2 2 A C A Ca b a+ = 3 3 2 3B π= 3 tan ( sin 2 cos ) cos2 2 2 2 A C A Ca b a+ = cos sin2 A Ca b A + = 1cos 2 2 B = B B ac 1 ( )2BD BA BC= +   BD BD tan ( sin 2 cos ) cos2 2 2 2 A C A Ca b a+ = sin ( sin 2 cos ) cos cos2 2 2 2 2 A C A A Ca b a+ = 即 ，即 . 由正弦定理得 ，因 ， 所以 ，则 ， 所以 ， 所以 ，即 . （2）由△ABC 的面积为 ，即 ，得 . 因为 D 为边 AC 的中点，所以 ，所以 ， 即 ， 当且仅当 时取“=”，所以 ，即线段 BD 长的最小值为 . 【点睛】 本题考查了三角恒等变换，面积公式和基本不等式，考查了转化思想和方程思想，属于 中档题． 18．已知正方形 ABCD，E，F 分别为 AB，CD 的中点，将△ADE 沿 DE 折起，使△ACD 为等边三角形，如图所示，记二面角 A-DE-C 的大小为 . （1）证明：点 A 在平面 BCDE 内的射影 G 在直线 EF 上； （2）求角 的正弦值. 【答案】（1）见解析；（2） . 【解析】（1）过点 作 平面 ，垂足为 ，连接 ， ．证明 在 的垂直平分线上，则点 在平面 内的射影 在直线 上， （2）以 点为坐标原点，以 所在直线为 轴， 所在直线为 轴，过 点作平 (cos cos sin sin ) 2 sin cos2 2 2 2 2 2 A C A C A Aa b− = cos sin2 A Ca b A + = sin cos sin sin2 A CA B A + = 0 ,sin 0,sin 02 BA Aπ< < ≠ ≠ cos sin2 A C A + = sin sin 2sin cos2 2 2 B B BB= = 1cos (0 )2 2 2 2 B B π= < < 2 3 B π= 2 3B π= 3 3 1 sin 3 32 ac B = 12ac = 1 ( )2BD BA BC= +   2 2 21 ( 2 )4BD BA BC BA BC     = + + 2 2 21 1 1( 2 cos ) (2 ) 34 4 4BD c a ac B ac ac ac = + + ≥ − = = 2 3a c= = 3BD ≥ 3 ( )0θ θ π< < θ 15sin 4 θ = A AG ⊥ BCDE G GC GD G CD A BCDE G EF G GA z GF y G 行于 的向量为 轴建立空间直角坐标系．设正方形 的边长为 ，分别求出 平面 与平面 的一个法向量，由两法向量所成角的余弦值可得角 的正弦 值． 【详解】 （1）证明：过点 A 作 AG⊥平面 BCDE，垂足为 G，连接 GC，GD. 因为△ACD 为等边三角形，所以 AC=AD，所以点 G 在 CD 的垂直平分线上. 又因为 EF 是 CD 的垂直平线，所以点 A 在平面 BCDE 内的射影 G 在直线 EF 上. 另证：过点 A 作 AG⊥EF，再证 AG⊥CD，从而证得 AG⊥平面 BCDE， 即点 A 在平面 BCDE 内的射影 G 在直线 EF 上 （2）解：以 G 为坐标原点，GA 所在直线为 z 轴，GF 所在直线为 y 轴，过点 G 作平行 于 DC 的直线为 x 轴建立空间直角坐标系. 设正方形 ABCD 的边长为 2a，连接 AF， 则 ， ， 所以 设平面 的一个法向量为 ，则 ， 令 ，得 ，又平面 的一个法向量 所以 ， . 【点睛】 本题考查直线与平面垂直的判定，考查空间想象能力与思维能力，训练了二面角的平面 DC x ABCD 2a DEC ADE θ 3AF a= AE a= 2EF a= 3 3 3(0,0,0), (0,0, ), ( , ,0), ( , ,0), (0, ,0)2 2 2 2 aG A a C a a D a a E- - ADE ( ), ,m x y z= 3 3 02 2 · 2 0 m AD ax ay az m DE ax ay  ⋅ = + − =  = + =   1y = 32,1, 3m æ ö÷ç ÷= - -ç ÷ç ÷÷çè ø CDE ( )0,0,1n = 1cos 4 m n m n     q = = 15sin 4 θ∴ = 角的求法，属于中档题． 19．如图，已知椭圆 的长轴 ，长为 4，过椭圆的右焦点 作斜 率为 （ ）的直线交椭圆于 、 两点，直线 ， 的斜率之积为 . （1）求椭圆 的方程； （2）已知直线 ，直线 ， 分别与 相交于 、 两点，设 为线段 的中点， 求证： . 【答案】（1） ；（2）证明见解析. 【解析】（1）由长轴长为 4 可得 a，设出点 B，C 的坐标，利用斜率之积为 ，可得 ，即可得到 b2，可得椭圆方程； （2）设直线 BC 的方程为：y＝k（x﹣1）与椭圆方程联立，得到根与系数的关系，直线 的方程为：y （x+2）与 x=4 联立，可得点 M，N 的坐标，可得线段 MN 的中 点 E．利用根与系数的关系及其斜率计算公式可得 ，只要证明 1 即可． 【详解】 （1）设 ， ，因点 在椭圆上，所以 ， 故 .又 ， ， 所以 ，即 ，又 ，所以 故椭圆 的方程为 . （2）设直线 的方程为： ， ， ， 联立方程组 ，消去 并整理得， ，则 ， . 直线 的方程为 ，令 得 ， 同理， ； 所以 ， 代入化简得 ，即点 ，又 ， 所以 ，所以 . 【点睛】 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、斜率计算公式、相互垂直 的直线斜率之间的关系，考查了推理能力与计算能力，属于难题． 20．已知函数 . （1）当 时，求函数 在区间 上的值域. （2）对于任意 ，都有 ，求实数 的取值范 围. 【答案】(1) (2) 【解析】试题分析：（1）先求导数，再求 导数，得 从而确定 ，再根据 单调性得值域（2）先整理不等 式得 ，转化为函数 在区间 为增函数，再转化为对应函数导数恒非负， 分离变量得 最小值，最后利用导数求函数 单调性， 得最值，即得实数 的取值范围. 试题解析：（1）当 时， ， ， 令 ，有 ， ( ) ( )e sin 2 R2 xf x ax x a π = + − − ∈   1a = ( )f x [ ],π π− 1 20 x x π< < < ( ) ( ) 2 1 2 1 2e e 2x x f x f x a π− > − −− a ( ) ( )4 e 3 4 e,2 2 π ππ π − − +−    1a π≥ ( ) sin cos 12g x x x x π= + + − − ( ) 02g x g π ≤ =   ， ( ) 0f x′ ≤ ( )f x ( ) ( )2 1 2 12 e 2 e2 2 x xf x a f x a π π   − − − > − − −       ( ) ( ) 2 e2 xG x f x a π = − − −   ( )0,π sin cosx xa x +− ≤ ( ) sin cosx xh x x += a 1a = ( ) e sin 22 xf x x x π = + − −   ( ) e sin cos 12 xf x x x x π = + + − − ′  ( ) sin cos 12g x x x x π= + + − − ( ) 1 cos sin 1 2sin 4g x x x x π = + − = −′ −    当 时， ， 当 时 ， 得 ，解得： ， 故当 时，函数 单调递减，当 时，函数 单调递增， 所以当 时， ，可得 ， 函数 在区间 上单调递减， ， ， 故函数 在区间 上的值域为 . （2）由 ，有 ， 故 可化为 ， 整理为： ， 即函数 在区间 为增函数， ， ，故当 时， ， 即 ， ①当 时， ； ②当 时，整理为： ， 令 ，有 xπ π− ≤ ≤ 5 3 4 4 4x ππ π− ≤ − ≤ ( ) 0g x′ < 2sin 4 2x π − >   3 4 4 4x π π π≤ − ≤ 2 x π π≤ ≤ 2 x π π≤ ≤ ( )g x 2x ππ− ≤ ≤ ( )g x xπ π− ≤ ≤ ( ) 02g x g π ≤ =   ( ) 0f x′ ≤ ( )f x [ ],π π− ( ) ( ) ( ) min 4 ee 22 2f x f π π πππ − = = − =   ( ) ( ) ( ) max 3 4 e3e 22 2f x f π π πππ − − + = − = − − = −   ( )f x [ ],π π− ( ) ( )4 e 3 4 e,2 2 π ππ π − − +−    1 20 x x π< < < 2 1e e 0x x− > ( ) ( ) 2 1 2 1 2e e 2x x f x f x a π− > − −− ( ) ( ) ( )2 1 2 1 2 e e2 x xf x f x a π − > − − −   ( ) ( )2 1 2 12 e 2 e2 2 x xf x a f x a π π   − − − > − − −       ( ) ( ) 2 e2 xG x f x a π = − − −   ( )0,π ( ) e sin 22 xG x ax x π = + − − −   ( )2 e e sin2 x xa ax x a π − − = + −   ( ) ( )e sin cosxG x ax x x=′ + + [ ]0,x π∈ ( ) 0G x′ ≥ sin cos 0ax x x+ + ≥ 0x = Ra∈ 0 x π< ≤ sin cosx xa x +− ≤ ( ) sin cosx xh x x += ( ) ( ) ( ) 2 cos sin sin cosx x x x xh x x − − +=′ ， 当 ， ， ，有 ， 当 时，由 ，有 ，可得 ， 由上知 时，函数 单调递减， 故 ， 故有： ，可得 . 点睛：利用导数研究不等式恒成立或存在型问题，首先要构造函数，利用导数研究函数 的单调性，求出最值，进而得出相应的含参不等式，从而求出参数的取值范围；也可分 离变量，构造函数，直接把问题转化为函数的最值问题. 21．随着科学技术的飞速发展，网络也已经逐渐融入了人们的日常生活，网购作为一种 新的消费方式，因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可. 某网购公司统计了近五年在本公司网购的人数，得到如下的相关数据(其中“x=1”表示 2015 年，“x=2”表示 2016 年，依次类推；y 表示人数)： x 1 2 3 4 5 y(万人) 20 50 100 150 180 （1）试根据表中的数据，求出 y 关于 x 的线性回归方程，并预测到哪一年该公司的网 购人数能超过 300 万人； （2）该公司为了吸引网购者，特别推出“玩网络游戏，送免费购物券”活动，网购者可 根据抛掷骰子的结果，操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本 营”，则网购者可获得免费购物券 500 元；若遥控车最终停在“失败大本营”，则网购者 可获得免费购物券 200 元. 已知骰子出现奇数与偶数的概率都是 ，方格图上标有第 0 格、第 1 格、第 2 格、…、第 20 格。遥控车开始在第 0 格，网购者每抛掷一次骰子， 遥控车向前移动一次.若掷出奇数，遥控车向前移动一格（从 到 ）若掷出偶数遥 控车向前移动两格（从 到 ），直到遥控车移到第 19 格胜利大本营）或第 20 格 （失败大本营）时，游戏结束。设遥控车移到第 格的概率为 ，试证明 ( ) ( ) 2 1 cos 1 sinx x x x x − − += 0 1x< < ( )1 cos 0x x− < ( )1 sin 0x x+ > ( ) 0h x′ < 1 x π≤ ≤ cos sinx x≤ ( ) ( )1 cos 1 sinx x x x− − + ≤ ( ) ( )1 sin 1 sin 2sin 0x x x x x− − + = − < ( ) 0h x′ < 0 x π< ≤ ( )h x ( ) ( )min sin cos 1h x h π ππ π π += = = − 1a π− ≤ − 1a π≥ 1 2 k 1k + k 2k + (1 19)n n≤ ≤ nP 是等比数列，并求网购者参与游戏一次获得免费购物券金额的期望值. 附：在线性回归方程 中， . 【答案】（1） ，预计到 2022 年该公司的网购人数能超过 300 万人； （2）约 400 元. 【解析】（1）依题意，先求出 ，代入公式即 可得到 ， ，可得回归方程为 ，令 ， ．所 以预计到 2022 年该公司的网购人数能超过 300 万； （2）遥控车移到第 （ ）格的情况是下列两种，而且也只有两种. ①遥控车先到第 格，又掷出偶数，其概率为 ②遥控车先到第 格，又掷出奇数，其概率为 所以 ，即可证得 是等比数列， 利用累加法求出数列 的通项公式，即可求得失败和获胜的概率，从而计算出期望. 【详解】 解：（1） 故 从而 所以所求线性回归方程为 ， 令 ，解得 . 故预计到 2022 年该公司的网购人数能超过 300 万人 （2）遥控车开始在第 0 格为必然事件， ，第一次掷骰子出现奇数，遥控车移到 { }1n nP P −− ˆˆ ˆy bx a= + 1 2 2 1 ˆ ˆˆ, n i i i n i i x y nx y b a y b x x nx = = − = = − − ∑ ∑ ˆ 42 26y x= − 5 5 2 1 1 3, 100, 1920, 55,i i i i i x y x y x = = = = = =∑ ∑ b a  42 26y x= − 42 26 300x − > 8x N x+∈ ⇒  n 2 19n  2n − 2 1 2 nP − 1n − 1 1 2 nP − 2 1 1 1 2 2n nnP P P− −= + { }1n nP P −− { }nP 1 2 3 4 5 3,5x + + + += = 20 50 100 150 180 1005y + + + += = 5 1 1 20 2 50 3 100 4 150 5 180 1920i i i x y = = × + × + × + × + × =∑ 5 2 2 2 2 2 2 1 1 2 3 4 5 55,i i x = = + + + + =∑ 1920 5 3 100 42,55 5 9b − × ×= =− ×  100 42 3 26,a y bx= − = − × = −  42 26y x= − *42 26 300,x x N− > ∈ 8x ≥ 0 1P = 第一格，其概率为 ,即 .遥控车移到第 （ ）格的情况是下列两种，而 且也只有两种. ①遥控车先到第 格，又掷出奇数，其概率为 ②遥控车先到第 格，又掷出偶数，其概率为 所以 ， 当 时，数列 是公比为 的等比数列 以上各式相加，得 （ ）， 获胜的概率 失败的概率 设参与游戏一次的顾客获得优惠券金额为 元， 或 X 的期望 参与游戏一次的顾客获得优惠券金额的期望值为 ，约 400 元. 【点睛】 本题考查了线性回归方程的求法与应用问题，等比数列的证明，等比数列求和公式，累 加法求数列的通项公式以及数学期望的计算，属于难题． 22．己知直线 的参数方程为 （t 为参数），曲线 C 的极坐标方程为 ，直线 与曲线 C 交于 A、B 两点，点 ． （1）求直线 的普通方程和曲线 C 的直角坐标方程； （2）求 的值． 1 2 1 1 2P = n 2 19n  2n − 2 1 2 nP − 1n − 1 1 2 nP − 2 1 1 1 2 2n nnP P P− −= + 1 1 2 1 ( )2n n n nP P P P− − −∴ − = − − ∴ 1 19n  1{ }n nP P −− 1 2 − 2 3 1 2 1 3 2 1 1 1 1 11 , ( ) , ( ) , ( )2 2 2 2 n n nP P P P P P P −∴ − = − − = − − = − ⋅⋅⋅ − = − 2 31 1 1 11 ( ) ( ) ( ) ( )2 2 2 2 n nP − = − + − + − +⋅⋅⋅+ − = 1 1( ) 1 ( )3 2 n − − −   12 11 ( )3 2 n nP + ∴ = − −   0,1,2, ,19n = ⋅⋅⋅ ∴ 20 19 2 11 ( )3 2P  = − −   19 20 18 1 1 112 3 2P P  = = +  （ ） ∴ X 200X = 500 ∴ 20 19 192 1 1 1 1500 1 ( ) 200 1 ( ) 100 4 ( )3 2 3 2 2EX      = × − + × + = −           ∴ 191100 4 ( )2  −   l 1 3 2 x t y t = +  = + 2sin 16cos 0ρ θ θ− = l ( )13P ， l 1 1 PA PB + 【答案】（1） ， ；（2） . 【解析】（1）直线的参数方程消去 t 可求得普通方程。由直角坐标与极坐标互换公式 ，求得曲线 C 普通方程。（2）直线的参数方程改写为 （t 为参数），由 t 的几何意义求值。 【详解】 直线 l 的参数方程为 为参数 ，消去参数，可得直线 l 的普通方程 ， 曲线 C 的极坐标方程为 ，即 ，曲线 C 的直角坐 标方程为 ， 直线的参数方程改写为 （t 为参数）， 代入 ， ， ， ， ． 【点睛】 由直角坐标与极坐标互换公式 ，利用这个公式可以实现直角坐标与极坐 标的相互转化。 23．已知函数 ． （1）当 时，求不等式 的解集； （2）证明： ． 2 1y x= + 2 16y x= 8 10 35 2 2 2 cos sin x y x y ρ θ ρ θ ρ =  =  + = 51 5 2 53 5 x t y t  = +  = + ( )1 1 (t3 2 x t y t = +  = + ) y 2x 1= + 2ρsin θ 16cosθ 0− = 2 2ρ sin θ 16ρcosθ= 2y 16x= ( )2 51 5 2 53 5 x t y t  = +  = + 2y 16x= 24 4 5t t 7 05 5 − − = 1 2t t 5+ = 1 2 35t t 4 = − 1 2 1 2 t t1 1 8 10 PA PB t t 35 −+ = = 2 2 2 cos sin x y x y ρ θ ρ θ ρ =  =  + = ( ) 1 ( 1)f x x m x mm = − + + > 2m = ( ) 3f x > 1( ) 3( 1)f x m m + ≥− 【答案】（1） ；（2）见解析. 【解析】（1）分 3 段去绝对值解不等式组，再取并集； （Ⅱ）由题 ， ， ，所以 ， 当且仅当 时等号成立，再利用基本不等式可证． 【详解】 解：（1）当 时， ； ①当 时，原不等式等价于 ，解得 ； ②当 时，原不等式等价于 ，不等式无解； ③当 时，原不等式等价于 ，解得 ， 综上，不等式 的解集为 ； （2）证明：因为 ，所以 ，当且仅当 时 取“ ” 所以 当且仅当 且 时取“ ”，故得证. 【点睛】 本题考查了绝对值不等式的解法，属于中档题． 3 9( , ) ( , )4 4−∞ − +∞ 1( ) | | | |f x x m x m = − + + 1m > 1 1| |m mm m ∴ + = + 1( )f x m m + 1 ,x mm  ∈ −   2m = 1( ) | 2 | | |2f x x x= − + + 1 2x − 1(2 ) ( ) 32x x− − + > 3 4x < − 1 22 x− < < 5 32 > 2x 1( 2) ( ) 32x x− + + > 9 4x > ( ) 3f x > 3 9( , ) ( , )4 4−∞ − +∞ 1m > ( ) 1 1f x m mm m ≥ + = + 1 ,x mm  ∈ −   = ( ) 1 1 1 1 11 1 3( 1) ( 1) 1 1f x m m mm m m m m m m + ≥ + + = + = − + + ≥− − − − 2m = 1 ,22x  ∈ −   =