2014年高考真题——理科数学（广东卷）原卷版 8页

图 1 高中生 2000 名 小学生 3500 名 初中生 4500 名 图 2 近视率/ % 30 10 50 O 小学 初中 高中 年级 2014 年普通高等学校招生全国统一考试（广东卷） 数 学（理科） 一、选择题：本大题共 8 小题，每小题 5 分，满分 40 分，在每小题给出的四个选项中，只有一项是符合 题目要求的． 1．已知集合 { 1,0,1}M  ， {0,1,2}N  ，则 MN A．{0,1} B．{ 1,0,2} C．{ 1,0,1,2} D．{ 1,0,1} 2．已知复数 z 满足(3 4 ) 25iz，则 z  A． 34i B． 34i C．34i D．34i 3．若变量 ,xy满足约束条件 1 1 yx xy y      ≤ ≤ ≥ ，且 2z x y的最大值和最小值分别为 m 和 n ，则mn A．5 B．6 C．7 D．8 4．若实数 k 满足09k，则曲线 22 125 9 xy k 与曲线 22 125 9 xy k  的 A．焦距相等 B．实半轴长相等 C．虚半轴长相等 D．离心率相等 5．已知向量 (1,0, 1)a= ，则下列向量中与a 成60 夹角的是 A．( 1,1,0) B．(1, 1,0) C．(0, 1,1) D．( 1,0,1) 6．已知某地区中小学生人数和近视情况分别如图 1 和图 2 所示. 为了解该地区中小学生的近视形成原因， 用分层抽样的方法抽取 2 %的学生进行调查，则样本容量和抽取的高中生近视人数分别为 A．200，20 B．100，20 C．200，10 D．100，10 7．若空间中四条两两不同的直线 1 2 3 4, , ,l l l l ，满足 12ll ， 23ll ， 34ll ，则下列结论一定正确的是 A． 14ll B． 14//ll C． 1l 与 4l 既不垂直也不平行 D． 与 的位置关系不确定 8．设集合     1 2 3 4 5, , , , | 1,0,1 , 1,2,3,4,5iA x x x x x x i   　 ，那么集合 A 中满足条件 “ 1 2 3 4 513x x x x x   ≤ ≤ ”的元素个数为 A．60 B．90 C．120 D．130 A F E D C B 图 3 二、填空题：本大题共 7 小题，考生作答 6 小题，每小题 5 分，满分 30 分． （一）必做题（9 ~ 13 题） 9．不等式 1 2 5xx   ≥ 的解集为 ． 10．曲线 25   xey 在点 )3,0( 处的切线方程为 ． 11．从 0,1,2,3,4,5,6,7,8,9 中任取七个不同的数，则这七个数的中位数是 6 的概率为 ． 12．在 ABC 中，角 CBA ,, 所对应的边分别为 cba ,, . 已知 bBcCb 2coscos  ，则 b a ． 13．若等比数列 na 的各项均为正数，且 5 1291110 2eaaaa  ，则 1 2 20ln ln lna a a    ． （二）选做题（14 ~ 15 题，考生只能从中选做一题） 14．（坐标系与参数方程选做题）在极坐标系中，曲线 1C 和 2C 的方程分别为 2sin cos   和 sin 1 . 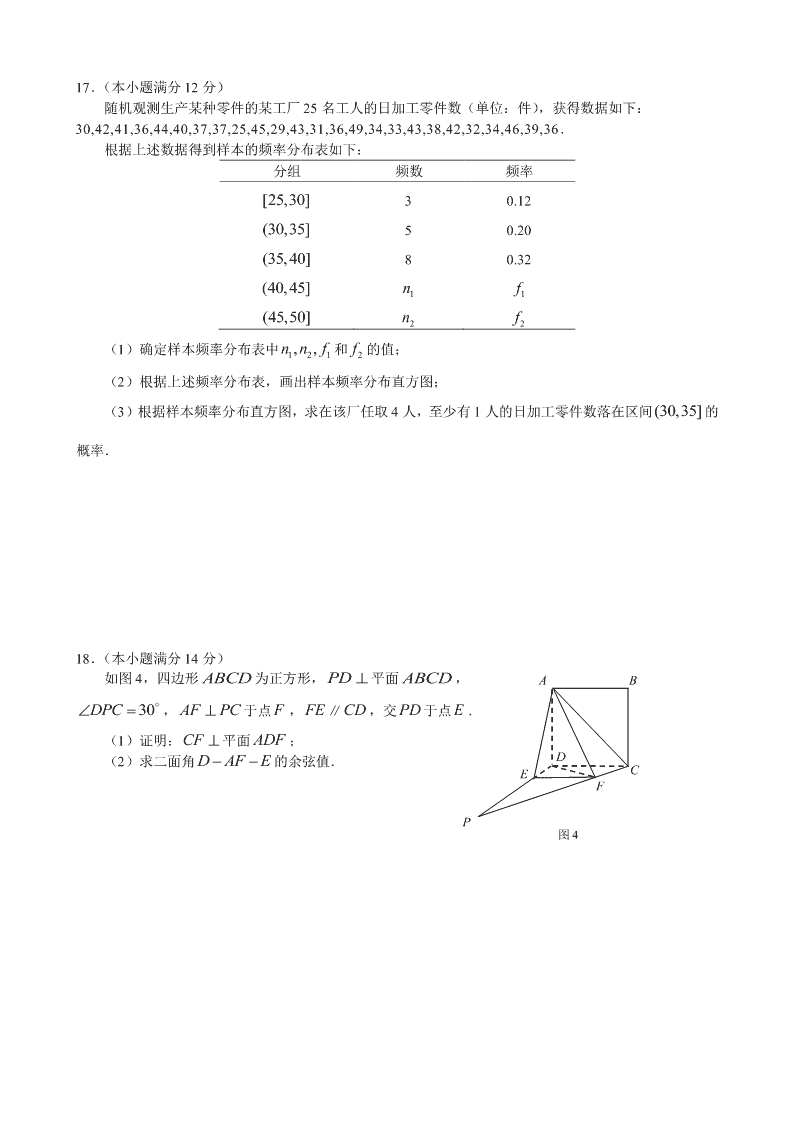以极点为平面直角坐标系的原点，极轴为 x 轴的正半轴，建立平面直角坐标系，则曲线 和 交点的直 角坐标为 ． 15．（几何证明选讲选做题）如图 3，在平行四边形 ABCD中，点 E 在 AB 上且 2EB AE ， AC 与 DE 交于点 F ，则 CDF AEF   的面积 的面积 ＝ ． 三、解答题：本大题共 6 小题，满分 80 分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分 12 分） 已知函数 ( ) sin( )4f x A x ， xR ，且 2 3)12 5( f ． （1）求 A 的值； （2）若 2 3)()(   ff ， )2,0(   ，求 )4 3(  f ． 图 4 P A B C E D F 17．（本小题满分 12 分） 随机观测生产某种零件的某工厂 25 名工人的日加工零件数（单位：件），获得数据如下： 30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36． 根据上述数据得到样本的频率分布表如下： 分组 频数 频率 [25,30] 3 0.12 (30,35] 5 0.20 (35,40] 8 0.32 (40,45] 1n 1f (45,50] 2n 2f （1）确定样本频率分布表中 1 2 1,,n n f 和 2f 的值； （2）根据上述频率分布表，画出样本频率分布直方图； （3）根据样本频率分布直方图，求在该厂任取 4 人，至少有 1 人的日加工零件数落在区间 的 概率． 18．（本小题满分 14 分） 如图 4，四边形 ABCD 为正方形， PD  平面 ， 30DPC， AF PC 于点 F ， FE ∥CD ，交 PD 于点 E ． （1）证明：CF  平面 ADF ； （2）求二面角 D AF E的余弦值． 19．（本小题满分 14 分） 设数列 na 的前 n 项和为 nS ， 满足 2 12 3 4nnS na n n   ， *nN ，且 3 15S  ． （1）求 1 2 3,,a a a 的值； （2）求数列 的通项公式． 20．（本小题满分 14 分） 已知椭圆 22 22:1xyC ab( 0)ab 的一个焦点为( 5,0) ，离心率为 5 3 ． （1）求椭圆C 的标准方程； （2）若动点 00( , )P x y 为椭圆 外一点，且点 P 到椭圆 的两条切线相互垂直，求点 的轨迹方程． 21.（本小题满分 14 分） 设函数 2 2 2 1() ( 2 ) 2( 2 ) 3 fx x x k x x k        ，其中 2k  ． （1）求函数 ()fx的定义域 D （用区间表示）； （2）讨论 ()fx在区间 上的单调性； （3）若 6k  ，求 上满足条件 ( ) (1)f x f 的 x 的集合（用区间表示）． x 2014 年普通高等学校招生全国统一考试（广东卷） 数 学（理科）参考答案 一、选择题：本大题共 8 小题，每小题 5 分，满分 40 分，在每小题给出的四个选项中，只有一项是符合 题目要求的． 题号 1 2 3 4 5 6 7 8 答案 C D B A B A D D 二、填空题：本大题共 7 小题，考生作答 6 小题，每小题 5 分，满分 30 分． （一）必做题（9 ~ 13 题） 9. ( , 3] [2, )   10. 5 3 0xy   11. 1 6 12. 2 13.50 （二）选做题（14 ~ 15 题，考生只能从中选做一题） 14.(1,1) 15.9 三、解答题：本大题共 6 小题，满分 80 分．解答须写出文字说明、证明过程和演算步骤． 16.（本小题满分 12 分） 16. 解：（1） 5 5 2 3 3( ) sin( ) sin12 12 4 3 2 2f A A A        ，解得 3A  . （2）由（1）得 ( ) 3sin( )4f x x ， 所以 ( ) ( ) 3sin( ) 3sin( )44ff          2 2 2 2 33( cos sin ) 3( cos sin ) 6 cos2 2 2 2 2          所以 6cos 4  ，又因为 )2,0(   ，所以 2 10sin 1 cos 4   ， 所以 3 3 10 30( ) 3sin( ) 3sin( ) 3sin 34 4 4 4 4f                 . 17.（本小题满分 12 分） 17. 解：（1） 1 7n  ， 2 2n  ， 1 7 0.2825f  ， 2 2 0.0825f  . （2）所求的样本频率分布直方图如图所示： （3）设“该厂任取 4 人，至少有 1 人的日加工零件数落在区间(30,35]”为事件 A ， 4( ) 1 (1 0.2) 0.5904PA    ，即至少有 1 人的日加工零件数落在区间 概率为0.5904 . 0 25 30 35 40 45 50 日加工零件数 频率 组距 0.040 0.024 0.016 0.056 0.064 P A B C E D F G H x y z 18．（本小题满分 14 分） 18.（1）证明：因为 PD 平面 ABCD， AD 平面 ，所以 PD AD . 因为在正方形 中CD AD ，又CD PD D ，所以 AD  平面 PCD. 因为CF 平面 PCD，所以 AD CF . 因为 AF CF ， AF AD A ，所以CF  平面 ADF . （2）方法一：以 D 为坐标原点， DP 、 DC 、 DA 分别为 x 、 y 、 z 轴建立空间直角坐标系 设正方形 的边长为 1， 则 3 3 3(0,0,0), (0,0,1), (0,1,0), ( 3,0,0), ( ,0,0), ( , ,0)4 4 4D A C P E F . 由（1）得 ( 3, 1,0)CP 是平面 BCDE 的一个法向量. 设平面 AEF 的法向量为 ( , , )x y zn ， 3(0, ,0)4EF  ， 3( ,0,1)4EA  ， 所以 3 04 3 04 EF y EA x z           n n . 令 4x  ，则 0y  ， 3z  ，所以 (4,0, 3)n 是平面 的一个法向量. 设二面角 D AF E的平面角为 ，且 (0, )2   所以 4 3 2 57cos 192 19 CP CP      n n ， 所以二面角 的平面角的余弦值为 2 57 19 . 方法二：过点 D 作 DG AE 于G ，过点 作 DH AF 于 H ，连接GH . 因为CD PD ，CD ED ， ED AD D ，所以CD  平面 ADE . 因为 FE ∥CD ，所以 FE 平面 . 因为 DG  平面 ，所以 FE DG . 因为 AE FE E ，所以 DG  平面 AEF . 根据三垂线定理，有GH AF ， 所以 DHG 为二面角 的平面角. 设正方形 的边长为 1， 在 Rt △ ADF 中， 1AD  ， 3 2DF  ，所以 21 7DH  . 在 △ ADE 中，因为 11 24FC CD PC，所以 13 44DE PD，所以 57 19DG  . 所以 226 133 133GH DH DG   ， 所以 2 57cos 19 GHDHG DH   ， 所以二面角 的平面角的余弦值为 . 19.（本小题满分 14 分） 19. 解：（1）当 2n  时， 2 1 2 34 20S a a a    ， 又 3 1 2 3 15S a a a    ，所以 334 20 15aa   ，解得 3 7a  . 当 1n  时， 1 1 227S a a   ，又 128aa，解得 123, 5aa. 所以 1 2 33, 5, 7a a a   . （2） 2 12 3 4nnS na n n   ① 当 2n≥ 时， 2 1 2( 1) 3( 1) 4( 1)nnS n a n n       ② ① ②得 12 (2 2) 6 1n n na na n a n     . 整理得 12 (2 1) 6 1nnna n a n     ，即 1 2 1 6 1 22nn nnaann . 猜想 21nan， *nN . 以下用数学归纳法证明： 当 时， 1 3a  ，猜想成立； 假设当 nk 时， 21kak， 当 1nk时， 2 1 2 1 6 1 2 1 6 1 4 1 6 1(2 1) 2 3 2( 1) 12 2 2 2 2kk k k k k k ka a k k kk k k k k                  ， 猜想也成立， 所以数列 na 的通项公式为 21nan， . 20.（本小题满分 14 分） 20. 解：（1）依题意得 5c  ， 5 3 ce a ， 所以 3a  ， 2 2 2 4b a c   ， 所以椭圆C 的标准方程为 22 194 xy （2）当过点 P 的两条切线 12,ll的斜率均存在时， 设 1 0 0: ( )l y y k x x   ，则 2 0 0 1: ( )l y y x xk    联立 22 00 194 () xy y y k x x       ， 得 2 2 2 0 0 0 0(4 9 ) 18 ( ) 9( ) 36 0k x k y kx x y kx       ， 所以 2 2 2 2 0 0 0 0(18 ) ( ) 4(4 9 )[9( ) 36] 0k y kx k y kx        ， 整理得 22 00( ) 4 9y kx k   ， 即 2 2 2 0 0 0 0( 9) 2 4 0x k x y k y     ， 因为 12ll ，所以 2 0 12 2 0 4 19 ykk x    ， 整理得 22 0013xy； 当过点 的两条切线 一条斜率不存在，一条斜率为 0 时， 为 (3, 2) 或( 3, 2) ，均满足 . 综上所述，点 的轨迹方程为 2213xy. 21.（本小题满分 14 分） 21. 解：（1） 22 1() ( 2 3)( 2 1) fx x x k x x k        ， 由 22( 2 3)( 2 1) 0x x k x x k       ，得 2 23x x k    或 2 21x x k   ， 即 2( 1) 2xk    或 2( 1) 2xk    ， 所以 1 2 1 2k x k          或 12xk     或 12xk     ，其中 2k  . 所以函数 ()fx的定义域 ( , 1 2) ( 1 2, 1 2) ( 1 2, )D k k k k                     . （2）令 2 2 2( ) ( 2 ) 2( 2 ) 3g x x x k x x k       ，则 1() () fx gx  ， xD 22( ) 2( 2 )(2 2) 2(2 2) 4( 1)( 2 1)g x x x k x x x x x k            ， 令 ( ) 0gx  ，解得 1 1xk    ， 2 1x  ， 3 1xk    ，其中 . 因为 131 2 1 2 1 1 2 1 2k x k k x k                       ， 所以 ( ), ( )g x g x 随 x 的变化情况如下表： x ( , 1 2)k     ( 1 2, 1)k     1 ( 1, 1 2)k     ( 1 2, )k     ()gx   0 ()gx ↘ ↗ 极大值 ↘ ↗ 因为函数 ()y f x 与 ()y g x 在区间 D 上的单调性相反， 所以 ()fx在 和 上是增函数， 在 和 上是减函数. （3）因为 ( 1 ) ( 1 )g x g x     ，所以 ( 1 ) ( 1 )f x f x     ， 所以函数 与 的图象关于直线 1x  对称， 所以 (1) ( 3)ff. 因为 6k  ，所以 1 2 3 1 1 2kk            . ①当 ( 1 2, 1 2)x k k         时， 要使 ( ) (1)f x f ，则 ( 1 2, 3) (1, 1 2)x k k           ； ②当 ( , 1 2) ( 1 2, )x k k            时， 令 ( ) (1)f x f ，即 ( ) (1)g x g ， 22( 2 3)( 2 1) ( 6)( 2)x x k x x k k k         ， 令 2 2t x x k   ( 1)t  ，则( 3)( 1) ( 6)( 2)t t k k     ， 整理得 222 ( 8 15) 0t t k k     ，即[ ( 3)][ ( 5)] 0t k t k     ， 因为 1t  且 ，所以 ( 5)tk   ，即 2 25x x k k     ， 所以 2 2 2 5 0x x k    ，解得 1 2 4xk     ( , 1 2) ( 1 2, )kk            ， 所以 ( ) (1) ( 1 2 4)f x f f k      . 要使 ，则 ( 1 2 4, 1 2) ( 1 2, 1 2 4)x k k k k                  . 综上所述，当 时，在 D 上满足条件 的 x 的集合为 ( 1 2 4, 1 2) ( 1 2, 3) (1, 1 2) ( 1 2, 1 2 4)k k k k k k                            .