2018-2019学年黑龙江省大庆十中高二上学期第一次月考数学试题（Word版） 8页

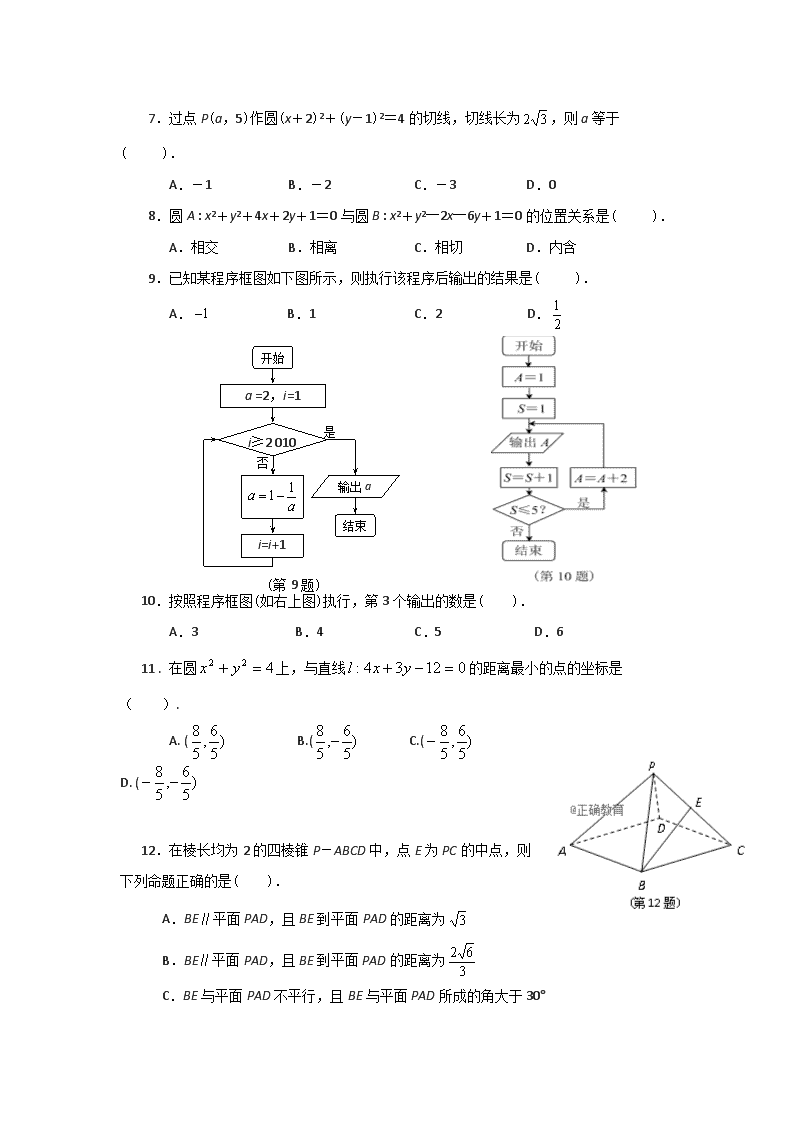
‎2018-2019学年黑龙江省大庆十中高二上学期第一次月考数学试题 ‎ (时间：120分钟　满分：150分)‎ 注意事项：‎ ‎1．答题前填写好自己的姓名、班级、考号等信息 ‎2．请将答案正确填写在答题卡上 第I卷（选择题）‎ 一、选择题(本大题共12小题，每小题5分，共60分)‎ ‎1．点(1，－1)到直线x－y＋1＝0的距离是( )．‎ A． B． C． D．‎ ‎2．下列直线中与直线2x＋y＋1＝0垂直的一条是( ).‎ A．2x―y―1＝0 B．x－2y＋1＝0 C．x＋2y＋1＝0 D．x＋y－1＝0‎ ‎3．已知圆的方程为x2＋y2－2x＋6y＋8＝0，那么通过圆心的一条直线方程是( )．‎ A．2x－y－1＝0 B．2x＋y＋1＝0 C．2x－y＋1＝0 D．2x＋y－1＝0‎ ‎4．下面程序输出结果是( )．‎ A．1，1 B．2，1 C．1，2 D．2，2‎ ‎5．把88化为五进制数是( )．‎ A．324(5) B．323(5) C．233(5) D．332(5)‎ ‎6．直线3x＋4y－5＝0与圆2x2＋2y2―4x―2y＋1＝0的位置关系是( )．‎ A．相离 B．相切 ‎ C．相交但直线不过圆心 D．相交且直线过圆心 ‎7．过点P(a，5)作圆(x＋2)2＋(y－1)2＝4的切线，切线长为，则a等于( )．‎ A．－1 B．－2 C．－3 D．0‎ ‎8．圆A : x2＋y2＋4x＋2y＋1＝0与圆B : x2＋y2―2x―6y＋1＝0的位置关系是( )．‎ A．相交 B．相离 C．相切 D．内含 ‎9．已知某程序框图如下图所示，则执行该程序后输出的结果是( )．‎ A． B．1 C．2 D．‎ 开始 a =2，i=1‎ i≥2 010‎ i=i+1‎ 结束 输出a 是 否 ‎(第9题)‎ ‎10．按照程序框图(如右上图)执行，第3个输出的数是( )．‎ A．3 B．4 C．5 D．6‎ ‎11 . 在圆上，与直线的距离最小的点的坐标是（ ）.‎ ‎ A. ( B.( C.( D. (‎ ‎12．在棱长均为2的四棱锥P－ABCD中，点E为PC的中点，则下列命题正确的是( )．‎ A．BE∥平面PAD，且BE到平面PAD的距离为 B．BE∥平面PAD，且BE到平面PAD的距离为 C．BE与平面PAD不平行，且BE与平面PAD所成的角大于30°‎ D．BE与平面PAD不平行，且BE与平面PAD所成的角小于30°‎ 第II卷（非选择题）‎ 二、填空题(本大题共4小题，每小题5分，共20分)‎ ‎13．960与1 632的最大公约数为 ．‎ ‎14．用秦九韶算法计算多项式f(x)＝12＋35x－8x2＋79x3＋6x4＋5x5＋3x6当x＝－4时，乘法运算的次数为 . ‎ ‎15．已知实数满足，则的最小值等于____________． ‎ ‎16．若圆C : x2＋y2－4x＋2y＋m＝0与y轴交于A，B两点，且∠ACB＝90，则实数m的值为__________．‎ 三、解答题(本大题共6小题，共70分)‎ ‎17．(本小题10分) 直线l经过直线x＋y－2＝0和直线x－y＋4＝0的交点，且与直线3x－2y＋4＝0平行，求直线l的方程.‎ ‎18．(本小题12分) 如图，ABCD是正方形，O是该正方形的中心，P是平面ABCD外一点，PO底面ABCD，E是PC的中点． ‎ 求证：(1)PA∥平面BDE ；‎ ‎(2)BD⊥平面PAC．‎ ‎19．(本小题12分) 求圆心在直线2x＋y＝0上，且圆与直线x＋y－1＝0切于点 M(2，－1)的圆的方程．‎ ‎ 20．(本小题12分) 在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD是菱形，∠BAD=60 °， AB =2，PD=，O为AC与BD的交点，E为棱PB上一点．‎ ‎（Ⅰ）证明：平面EAC⊥平面PBD；‎ ‎（Ⅱ）若PD∥平面EAC，求三棱锥P﹣EAD的体积．‎ ‎(第20题)‎ ‎21．(本小题12分) 在四面体ABCD中，△ABC与△DBC都是边长为4的正三角形．‎ ‎(1)求证：BC⊥AD；‎ ‎(2)若点D到平面ABC的距离等于3，求二面角A－BC－D的正弦值．‎ ‎22．(本小题12分) 已知圆C：x2+y2+4x﹣6y﹣3=0．‎ ‎（1）求过点M（﹣6，﹣5）的圆C的切线方程；‎ ‎（2）过点N（1，3）作直线与圆C交于A、B两点，求△ABC的最大面积及此时直线AB的 斜率．‎ ‎2018-2019学年度第一学期第一次检测 高二数学试卷 参考答案 一、选择题：‎ ‎1-6 DBBBBD 7-12 BCACAD 二、填空题：‎ ‎13．96 14. 6 15. 16. -3‎ 三、解答题：‎ ‎17．3x－2y＋9＝0‎ 试题解析：由，得. ‎ 即直线l过点(－1,3). ‎ ‎∵直线l的斜率为，∴直线l的方程为y－3＝ (x＋1)，即3x－2y＋9＝0. ‎ 解法二：由题意可设直线l的方程为x－y＋4＋λ(x＋y－2)＝0，‎ 整理得(1＋λ)x＋(λ－1)y＋4－2λ＝0，‎ ‎∵直线l与直线3x－2y＋4＝0平行，‎ ‎∴－2(1＋λ)＝3(λ－1)，∴λ＝. ‎ ‎∴直线l的方程为x－y＋＝0，即3x－2y＋9＝0. ‎ ‎18．证明：(1)连接EO，∵ 四边形ABCD为正方形，‎ ‎∴ O为AC的中点．‎ ‎∵ E是PC的中点，∴ OE是△APC的中位线．‎ ‎∴ EO∥PA．∵ EO平面BDE，PA平面BDE，‎ ‎∴ PA∥平面BDE． ‎ ‎(2)∵ PO⊥平面ABCD，BD平面ABCD， ‎ ‎∴ PO⊥BD．‎ ‎∵ 四边形ABCD是正方形， ‎ ‎∴ AC⊥BD．‎ ‎∵ PO∩AC＝O，AC 平面PAC，PO 平面PAC，‎ ‎∴ BD⊥平面PAC．‎ ‎19．解：因为圆与直线x＋y－1＝0切于点M(2，－1)，‎ 所以圆心必在过点M(2，－1)且垂直于x＋y－1＝0的直线l上．‎ 则l的方程为y＋1＝x－2，即y＝x－3．‎ 由 解得 即圆心为O1(1，－2)，半径r＝＝．‎ 故所求圆的方程为(x－1)2＋(y＋2)2＝2．‎ ‎20．（Ⅰ）证明：∵平面，平面，‎ ‎∴．∵四边形是菱形，∴，‎ 又∵，平面．‎ 而平面，∴平面平面．‎ ‎（Ⅱ）解：∵平面，平面平面，‎ ‎∴，‎ ‎∵是中点，∴是中点．‎ 取中点，连结，∵四边形是菱形，，‎ ‎∴，又，，∴平面，．‎ ‎∴．‎ 考点：（1）面面垂直的判定；（2）几何体的体积.‎ ‎21．证明：(1)取BC中点O，连结AO，DO．‎ ‎∵△ABC，△BCD都是边长为4的正三角形，‎ ‎∴AO⊥BC，DO⊥BC，且AO∩DO＝O，‎ ‎∴BC⊥平面AOD．又AD平面AOD，‎ ‎∴BC⊥AD． ‎ 解：(2)由(1)知∠AOD为二面角A－BC－D的平面角，设∠AOD＝q，则过点D作DE⊥AD，垂足为E．‎ ‎∵BC⊥平面ADO，且BC平面ABC，‎ ‎∴平面ADO⊥平面ABC．又平面ADO∩平面ABC＝AO，‎ ‎∴DE⊥平面ABC．‎ ‎∴线段DE的长为点D到平面ABC的距离，即DE＝3．‎ 又DO＝BD＝2，‎ 在Rt△DEO中，sinq＝＝，‎ 故二面角A－BC－D的正弦值为． ‎ ‎22．（1）或；（2）.‎ ‎【解析】圆：，即，表示以为圆心，半径等于的圆．由于点到圆心的距离等于，大于半径，故点在圆的外部．‎ 当切线的斜率不存在时，切线方程为符合题意．‎ 当切线的斜率存在时，设切线斜率为，则切线方程为，即，所以，圆心到切线的距离等于半径，即，解得，此时，切线为．‎ 综上可得，圆的切线方程为，或．‎ ‎（2）当直线的斜率不存在时，，，的面积 当直线的斜率存在时，设直线的方程为，即，‎ 圆心到直线AB的距离，‎ 线段的长度，‎ ‎∴的面积 当且仅当时取等号，此时，解得．‎ 所以，的最大面积为，此时直线的斜率为．‎ 考点：（1）圆的切线方程；（2）直线与圆的位置关系.‎