- 1.74 MB
- 2021-04-16 发布
2017-2018 学年甘肃省高台县第一中学下学期期中考试
高二文科数学
(考试时间:120 分钟 试卷满分:150 分)
测试范围:人教选修 1-1、1-2、4-4、4-5
第Ⅰ卷
一、选择题(本题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.已知点 A 的极坐标为 5π(2, )6
,则点 A 的直角坐标为
A. (1, 3) B. ( 1, 3) C. ( 3, 1)
D. ( 3,1)
2.已知i 为复数单位,则在复平面内复数 2
1 i
对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四
象限
3.用反证法证明命题“三角形的内角中至多有一个是钝角”时,要做的假设是
A.假设三角形的内角中至少有一个钝角 B.假设三角形的内角中至少有两个
钝角
C.假设三角形的三个内角中没有一个钝角 D.假设没有一个钝角或至少有两个
钝角
4.设 m , n均为非零的平面向量,则“存在负数 ,使得 m n ”是“ 0 m n ”的
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
5.已知曲线 3 2( ) 2f x x ax 在点 (1, (1))f 处的切线的倾斜角为 3
4
,则实数 a
A. 2 B. 1 C. 2 D.3
6.已知命题 0:p x R , 0
5sin 2x ;命题 :q x R , 2 1 0x x .则下列结论正
确的是
A. p 是真命题 B. p q 是假命题 C. p q 是真命题
D. p q 是真命题
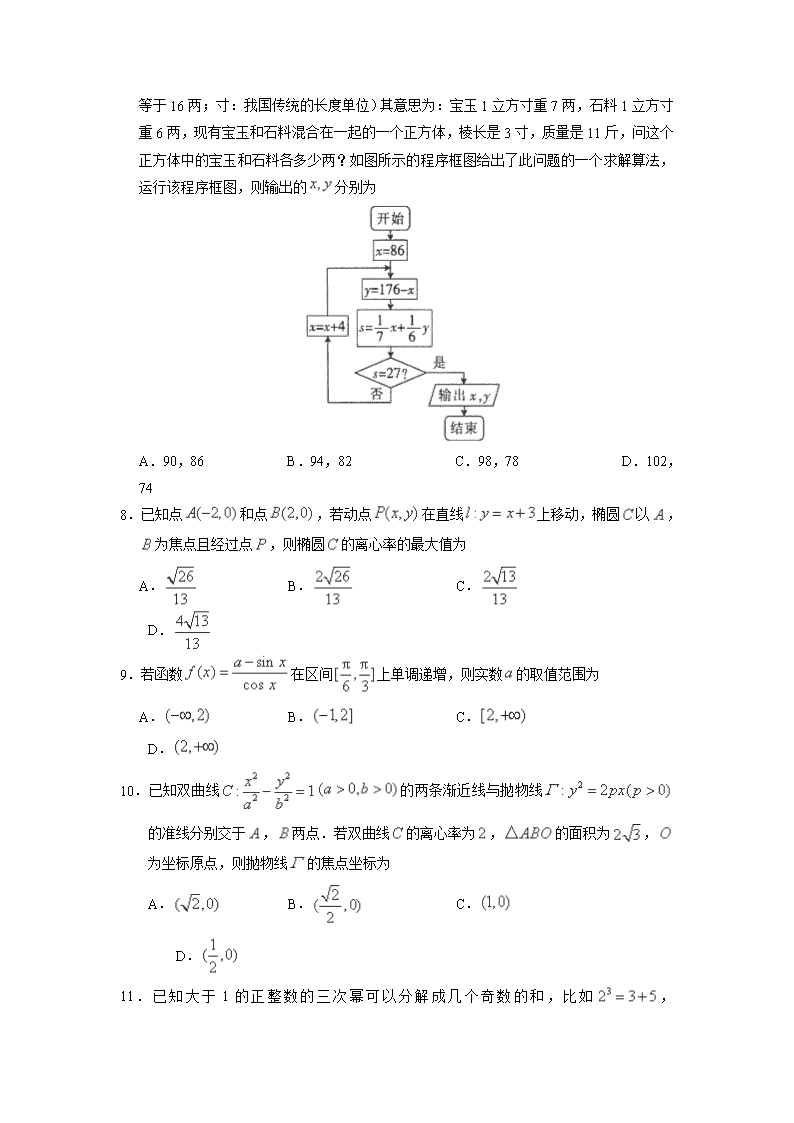
7.《九章算术》中的玉石问题:今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,
中有玉,并一十一斤,问玉、石各重几何?(斤、两:我国传统的质量单位,古代一斤
等于 16 两;寸:我国传统的长度单位)其意思为:宝玉 1 立方寸重 7 两,石料 1 立方寸
重 6 两,现有宝玉和石料混合在一起的一个正方体,棱长是 3 寸,质量是 11 斤,问这个
正方体中的宝玉和石料各多少两?如图所示的程序框图给出了此问题的一个求解算法,
运行该程序框图,则输出的 ,x y 分别为
A.90,86 B.94,82 C.98,78 D.102,
74
8.已知点 ( 2,0)A 和点 (2,0)B ,若动点 ( , )P x y 在直线 : 3l y x 上移动,椭圆C 以 A ,
B 为焦点且经过点 P ,则椭圆 C 的离心率的最大值为
A. 26
13
B. 2 26
13
C. 2 13
13
D. 4 13
13
9.若函数 sin( ) cos
a xf x x
在区间 π π[ , ]6 3
上单调递增,则实数 a 的取值范围为
A. ( ,2) B. ( 1,2] C.[2, )
D. (2, )
10.已知双曲线
2 2
2 2: 1x yC a b
( 0, 0)a b 的两条渐近线与抛物线 2: 2 ( 0)y px p
的准线分别交于 A , B 两点.若双曲线C 的离心率为 2 , ABO△ 的面积为 2 3 ,O
为坐标原点,则抛物线 的焦点坐标为
A. ( 2,0) B. ( 2 ,02 ) C. (1,0)
D. (1 ,02 )
11 . 已 知 大 于 1 的 正 整 数 的 三 次 幂 可 以 分 解 成 几 个 奇 数 的 和 , 比 如 32 3 5 ,
33 7 9 11 , 34 13 15 17 19 ,…,以此规律可知 345 分解后,和式中一定不
含有
A. 2069 B. 2039 C. 2009
D.1979
12.若存在正实数 , ,x y z ,使得 e
2
z xy
z
,且 2e
x z x ,则 ln y
x
的取值范围是
A. 1[1 ln2, ]2
B.[1 ln2,e 1 ln2] C.[ ln2,e 1 ln2]
D. 1[ ,1]2
第Ⅱ卷
二、填空题(本题共 4 小题,每小题 5 分,共 20 分)
13.已知i 为复数单位,若复数 z 的共轭复数 z 满足 (1 i) 3 iz ,则| |z ______________.
14.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了 5次试验,收
集到的数据如下表,由最小二乘法求得线性回归方程为 0 67 54 9ˆy x . .,则下表中污
损的数据为______________.
零件数 x (个) 10 20 30 40 50
加工时间 y (分
钟)
62 75 81 89
15.已知曲线 2 cos: sin
xC y
( 为参数),直线 1 3: 2 4
x tl y t
(t 为参数),若直线l 与曲
线C 交于 A , B 两点,则| |AB ______________.
16.某学校建议同学们周末去幸福广场看银杏叶,舒缓学习压力,返校后甲、乙、丙、丁四
位同学被问及情况.甲说:我没去;乙说:丁去了;丙说:乙去了;丁说:我没去.若
这四位同学中只有一位同学去了幸福广场,且只有一位同学说了假话,则去幸福广场的
这位同学是______________.
三、解答题(本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分 10 分)
已知函数 ( ) | 2 | | |,f x x a x a R .
(1)当 3a 时,求不等式 ( ) 3 0f x 的解集;
(2)若不等式 ( ) 1f x 恒成立,求实数 a 的取值范围.
18.(本小题满分 12 分)
现有一边长为 a 的正方形铁片,铁片的四角截去四个边长都为 x 的小正方形,然后做成
一个无盖方盒.
(1)试把方盒的容积V 表示为 x 的函数;
(2)当 x 为何值时,方盒的容积V 最大?并求出方盒的容积的最大值.
19.(本小题满分 12 分)
已知曲线 1C 的参数方程为
2
2
x t
y t
( t 为参数),以坐标原点为极点, x 轴的正半轴为
极轴建立极坐标系,曲线 2C 的极坐标方程为 cos sin 1 .
(1)求曲线 1C 的普通方程和曲线 2C 的直角坐标方程;
(2)设 (1,0)F ,曲线 2C 与曲线 1C 交于不同的两点 A , B ,求| | | |AF BF 的值.
20.(本小题满分 12 分)
已知函数 2( ) (2 )( 2)f x x x .
(1)求函数 ( )f x 的单调区间(用开区间表示);
(2)求函数 ( )f x 在区间 3[ 5, ]2
上的最大值与最小值.
21.(本小题满分 12 分)
2018 年为我国改革开放 40 周年,某事业单位共有职工 600 人,其年龄与人数分布表
如下:
年龄段 [22,35) [35,45) [45,55) [55,59]
人数(单位:
人) 180 180 160 80
若定义 45 岁至 59岁的为中年人,其余的为青年人,现按分层抽样抽取30人作为某庆
祝晚会的观众.
(1)若抽出的青年观众与中年观众中分别有12 人和5人不热衷关心民生大事,其余人
热衷关心民生大事.请将下面的 2 2 列联表补充完整,并判断是否有90%的把握认为
年龄层与是否热衷关心民生大事有关?
热衷关心民生大事
不热衷关心民生大
事
总计
青年观众 12
中年观众 5
总计 30
(2)在(1)的条件下,热衷关心民生大事的青年观众中有 1 人擅长歌舞,有 3 人擅长
乐器,现从热衷关心民生大事的青年观众中随机抽取 2 人上台进行才艺表演,求抽出的
2 人能胜任才艺表演的概率.
参考公式及数据:
2
2 ( )
( )( )( )( )
n ad bcK a b c d a c b d
,其中 n a b c d .
2
0( )P K k 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
22.(本小题满分 12 分)
已知椭圆
2 2
2 2: 1( 0)x y a ba b
的离心率为 2
2
, 1 2,F F 是椭圆 的两个焦点,A
为椭圆 上一点,且 1 2 3F AF , 1 2F AF△ 的面积为 3
3
.
(1)求椭圆 的标准方程;
(2)已知点 (0,1)P ,直线l 不经过点 P 且与椭圆交于 ,B C 两点,若直线 PB 与直线 PC 的
斜率之和为1,证明:直线l 过定点,并求出该定点的坐标.
高二文科数学·参考答案
13. 14. 68 15. 16.乙
21.(本小题满分 12 分)
【答案】(1)列联表见解析,没有 90% 的把握认为年龄层与是否热衷关心民生大事有关;
(2)
【解析】(1)由题可得抽出的青年观众有 18 人,中年观众有 12 人,
所以没有 90% 的把握认为年龄层与是否热衷关心民生大事有关.(6
分)
(2)热衷关心民生大事的青年观众有 6 人,记这 6 人分别为 A,
B,C,D,a,b,其中 A 表示擅长歌舞的青年观众,B,C,D 表
示擅长乐器的青年观众,
从这 6 人中随机抽取 2 人,有 AB,AC,AD,Aa,Ab,BC,BD,
Ba,Bb,CD,Ca,Cb,Da,Db,ab,共 15 种情况,(9 分)
其中能胜任才艺表演的有 AB,AC,AD,BC,BD,CD,共 6 种
情况,(10 分)
故所求概率 P= = = (12 分)