- 435.50 KB
- 2021-04-16 发布
2017-2018学年四川省眉山一中高二下学期期中考试
数学试卷(文)
命题人: 审题人:
一、选择题.(每小题5分,共60分)
1.东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,用分层抽样抽取一个容量为20的样本,则应抽取的后勤人员人数是( ).
A. 3 B. 2 C. 15 D. 4
2.复数=
A. B. C. D.
3.关于右侧茎叶图的说法,结论错误的一个是( )
A.甲的极差是29 B.甲的中位数是25
C.乙的众数是21 D.甲的平均数比乙的大
4.进入互联网时代,经常发送电子邮件,一般而言,发送电子邮件要分成以下几个步骤:(a).打开电子邮件;(b)输入发送地址;(c)输入主题;(d)输入信件内容;(e)点击“写邮件”;(f)点击“发送邮件”;正确的步骤是
A. B.
C. D.
5. 下列说法正确的是 ( )
A.某事件发生的概率为1.1 B.对立事件也是互斥事件
C.不能同时发生的的两个事件是两个对立事件
D.某事件发生的概率是随着实验次数的变化而变化的
6. 用反证法证明命题:“若,则函数至少有一
个零点”时,假设应为( )
A.函数没有零点 B.函数有一个零点
C.函数有两个零点 D.函数至多有一个零点
7. 下列说法中正确的是( )
A. 先把高三年级的2000名学生编号:1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为,然后抽取编号为的学生,这样的抽样方法是分层抽样法
B. 线性回归直线不一定过样本中心点
C. 若两个随机变量的线性相关性越强,则相关系数的值越接近于1
D. 若一组数据1、、3的平均数是2,则该组数据的方差是
8.为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算K2=8.01,附表如下:
P(K2≥k0)
0.100
0.050
0.025
0.010
0.001
k0
2.706
3.841
5.024
6.635
10.828
参照附表,得到的正确的结论是( )
A.有99%以上的把握认为“喜欢乡村音乐与性别有关”
B.有99%以上的把握认为“喜欢乡村音乐与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别无关”
9. 某广播电台只在每小时的整点和半点开始播送新闻,时长均为5分钟,则一个人在不知道时间的情况下打开收音机收听该电台,能听到新闻的概率是( )
A. B. C. D.
10. 已知 ,是虚数单位,则“”是“复数为纯虚数”的( )
A. 充分必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
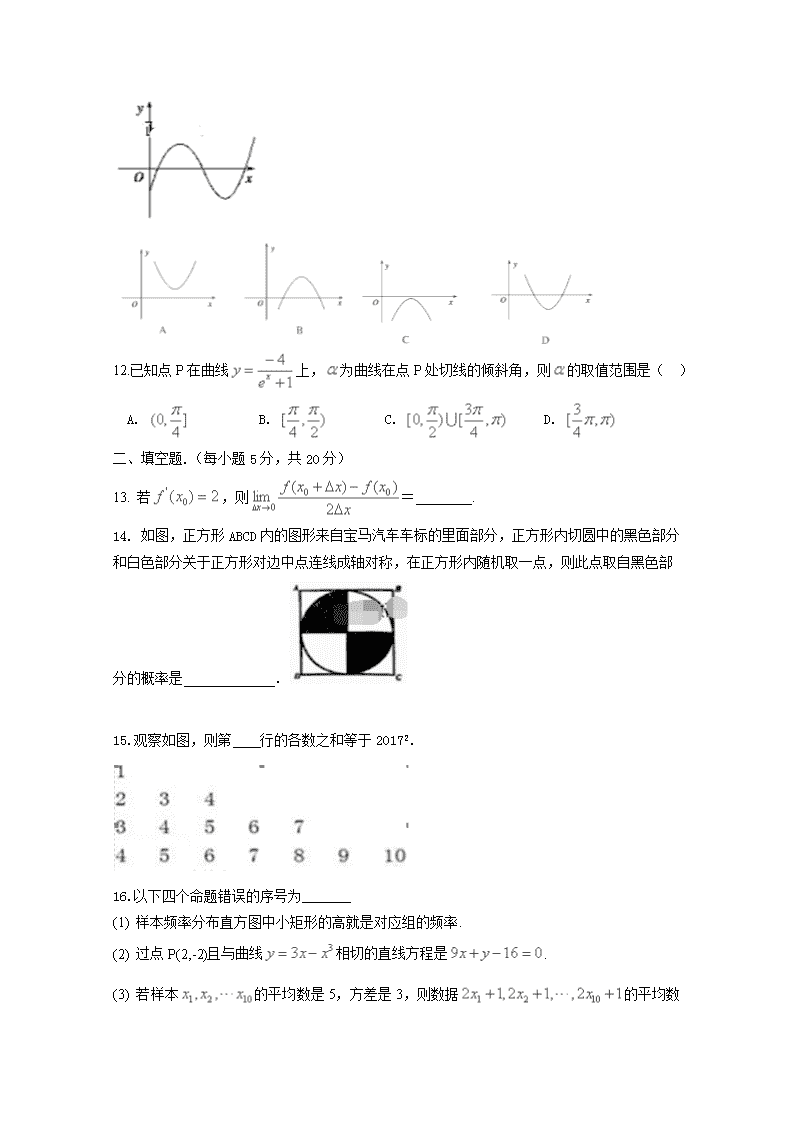
11. 函数f(x)在其定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象为( )
12.已知点P在曲线上,为曲线在点P处切线的倾斜角,则的取值范围是( )
A. B. C. D.
二、填空题.(每小题5分,共20分)
13. 若,则=________.
14. 如图,正方形ABCD内的图形来自宝马汽车车标的里面部分,正方形内切圆中的黑色部分和白色部分关于正方形对边中点连线成轴对称,在正方形内随机取一点,则此点取自黑色部分的概率是 .
15.观察如图,则第 行的各数之和等于20172.
16.以下四个命题错误的序号为_______
(1) 样本频率分布直方图中小矩形的高就是对应组的频率.
(2) 过点P(2,-2)且与曲线相切的直线方程是.
(3) 若样本的平均数是5,方差是3,则数据
的平均数是11,方差是12.
(4) 抛掷一颗质地均匀的骰子,事件“向上点数不大于4”和事件“向上点数不小于3”是对立事件.
三、解答题.(第17小题满分10分,其余各小题满分12分,共70分)
17.(本小题满分10分)已知复数z=(m﹣1)+(2m+1)i(m∈R)
(1)若复数z为纯虚数,求实数m的值;
(2)若复数z在复平面内的对应点位于第二象限,求 |z| 的最小值.
18.(本小题满分12分)已知函数
(1)分别求 的值;
(2)归纳猜想一般性结论,并给出证明.
19.(本小题满分12分)已知函数的图象过点,且在点处的切线方程为.
(1)求和的值; (2)求函数的解析式.
20.(本小题满分12分)某厂家为了了解某新产品使用者的年龄情况,现随机调査100 位使用者的年龄,整理后画出的频率分布直方图如图所示.
(1)求100名使用者中各年龄组的人数,
并利用所给的频率分布直方图估计所有使用者的平均年龄;
(2) 若已从年龄在的使用者中利用
分层抽样选取了6人,再从这6人中选出2人,
求这2人在不同的年龄组的概率.
21.(本小题满分12分)随着经济的发展,我市居民收入逐年增长,下表是我市一建设银行连续五年的储蓄存款(年底余额):
年份
2011
2012
2013
2014
2015
储蓄存款(千亿元)
5
6
7
8
10
为了研究计算的方便,工作人员将上表的数据进行了处理,,:
(1)填写下列表格并根据表格求关于的线性回归方程;
时间代号
(2)通过(Ⅰ)中的方程,求出关于的回归方程,并用所求回归方程预测到2020年年底,该银行储蓄存款额可达多少?
(附:对于线性回归方程,其中)
22. (本小题满分12分)已知函数
(1) 当时,求的单调区间;
(2)若存在单调递减区间,求的取值范围.
文科数学答案
一、选择题
1-6 A C B C B A 7-12 D A C B D A
二、填空题
13. 1 14. 15. 1009 16. (1)(2)(4)
三、解答题
17.解:(1)∵z=(m﹣1)+(2m+1)i(m∈R)为纯虚数,
∴m﹣1=0且2m+1≠0∴m=1
(2)z在复平面内的对应点为(m﹣1,2m+1))
由题意:,∴.
即实数m的取值范围是.
而|z|===,
当时, =.
18.解:(Ⅰ)
(Ⅱ)猜想:
证明:∵, ∴
∴ ∴
19.解:(1)∵f(x)在点M(﹣1,f(﹣1))处的切线方程为6x﹣y+7=0.
故点(﹣1,f(﹣1))在切线6x﹣y+7=0上,且切线斜率为6.
得f(﹣1)=1且f′(﹣1)=6.
(2)∵f(x)过点P(0,2)
∴d=2
∵f(x)=x3+bx2+cx+d
∴f′(x)=3x2+2bx+c
由f′(﹣1)=6得3﹣2b+c=6
又由f(﹣1)=1,得﹣1+b﹣c+d=1
联立方程得
故f(x)=x3﹣3x2﹣3x+2
20.解:(1)由图可得,各组年龄的人数分別为:10,30,40,20.
估计所有使用者的平均年龄为: (岁)
(2)由题意可知抽取的6人中,年龄在范围内的人数为4,记为;年龄在范围内的人数为2,记为.从这6人中选取2人,结果共有15种:
.
设“这2人在不同年龄组“为事件.
则事件所包含的基本事件有8种,故,所以这2人在不同年龄组的概率为.
21.解:
时间代号t
1
2
3
4
5
z
0
1
2
3
5
(1)
,
(2),代入得到:
,即
,
预测到2020年年底,该地储蓄存款额可达15.6千亿元
22.解:(1)当,
其定义域为(0,+∞),
∴f′(x)===
∵令,则;令,则,
∴是的单调递增区间, 是的单调递减区间,
(2)∵,
∴f′()== (>0).
∵存在单调递减区间,
∴在(0,+∞)上有解,
又∵>0,则在(0,+∞)上有解,
①当=0时,>1在(0,+∞)上有解;
②当>0时,在(0,+∞)上总有解;
③当<0时,要使在(0,+∞)上有解,
只需有两个不相等正实数根,
∴,解得
综上,的取值范围是.
注:此题还可用分离参数法转化为求最值