2020高中数学 每日一题之快乐暑假 第05天 初高中衔接：高次不等式（含解析）新人教A版 4页

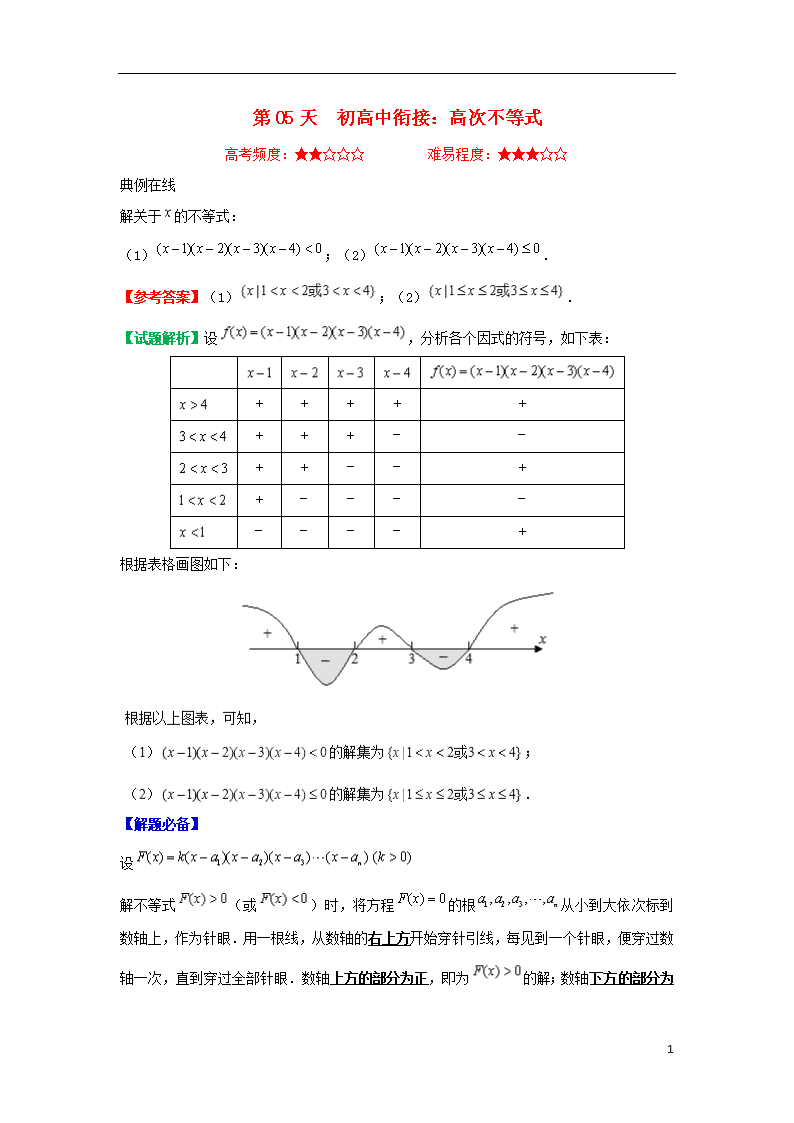
第05天 初高中衔接：高次不等式 高考频度：★★☆☆☆ 难易程度：★★★☆☆‎ 典例在线 解关于的不等式：‎ ‎（1）；（2）．‎ ‎【参考答案】（1）；（2）．‎ ‎【试题解析】设，分析各个因式的符号，如下表：‎ ‎+‎ ‎+‎ ‎+‎ ‎+‎ ‎+‎ ‎+‎ ‎+‎ ‎+‎ ‎–‎ ‎–‎ ‎+‎ ‎+‎ ‎–‎ ‎–‎ ‎+‎ ‎+‎ ‎–‎ ‎–‎ ‎–‎ ‎–‎ ‎–‎ ‎–‎ ‎–‎ ‎–‎ ‎+‎ 根据表格画图如下：‎ ‎ ‎ ‎ ‎ ‎【解题必备】‎ 设 解不等式（或）时，将方程的根从小到大依次标到数轴上，作为针眼．用一根线，从数轴的右上方开始穿针引线，每见到一个针眼，便穿过数轴一次，直到穿过全部针眼．数轴上方的部分为正，即为的解；数轴 4‎ 下方的部分为负，即为不等式的解．‎ 注意：‎ ‎（1）要求的最高次项系数为正；（即每一个的系数为正且，若，则不等式两边同时乘以，并改变不等号的方向）‎ ‎（2）当根为二重根（即两个相等的实数根）时，按两个针眼对待，即穿过数轴两次（简记为“奇过偶不过”）；‎ ‎（3），；‎ ‎，（或）；‎ ‎（4），当时，的符号是确定的；‎ ‎（5）永远从数轴右上方开始；‎ ‎（6）最后结果数轴上方的部分为不等式的解，数轴下方的部分为不等式的解；‎ ‎（7）不等式右边须为0，否则先移项，使右边为0；‎ ‎（8）穿针引线法可以用于解高次不等式，也可以用于解一次、二次不等式，或可以转化为高次不等式的分式不等式等． ‎ 学霸推荐 ‎1．解关于的不等式：‎ ‎（1）； （2）； （3）；‎ ‎（4）； （5）．‎ ‎2．解关于的不等式：‎ ‎（1）； （2）．‎ 4‎ ‎ ‎ ‎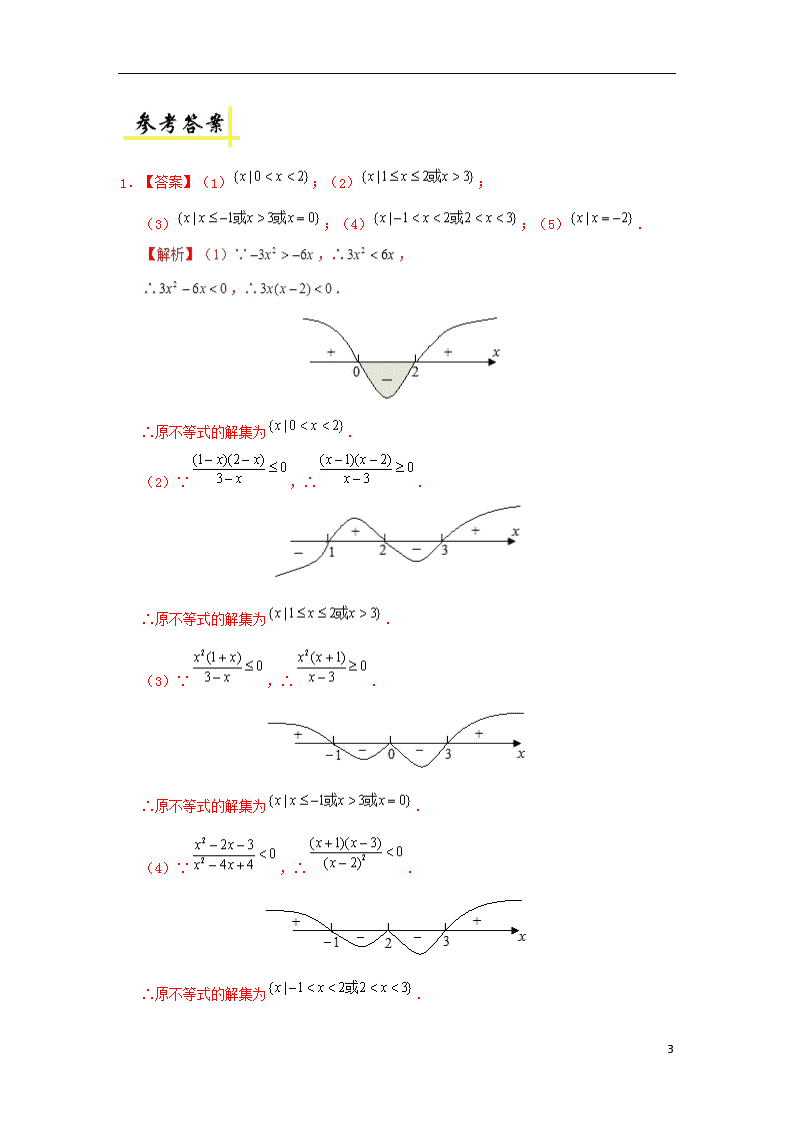1．【答案】（1）；（2）；‎ ‎（3）；（4）；（5）．‎ ‎ ‎ ‎ ‎ ‎∴原不等式的解集为．‎ ‎（2）∵，∴．‎ ‎ ‎ ‎∴原不等式的解集为．‎ ‎（3）∵，∴．‎ ‎ ‎ ‎∴原不等式的解集为．‎ ‎（4）∵，∴．‎ ‎ ‎ ‎∴原不等式的解集为．‎ 4‎ ‎（5）∵，∴．‎ ‎ ‎ ‎∴原不等式的解集为．‎ ‎2．【答案】（1）；（2）．‎ ‎ ‎ ‎ ‎ ‎∴原不等式的解集为．‎ ‎（2）∵，∴，∴，∴．‎ ‎ ‎ ‎∴原不等式的解集为．‎ 4‎