2018-2019学年浙江省慈溪市六校高二上学期期中考试数学试题 Word版 10页

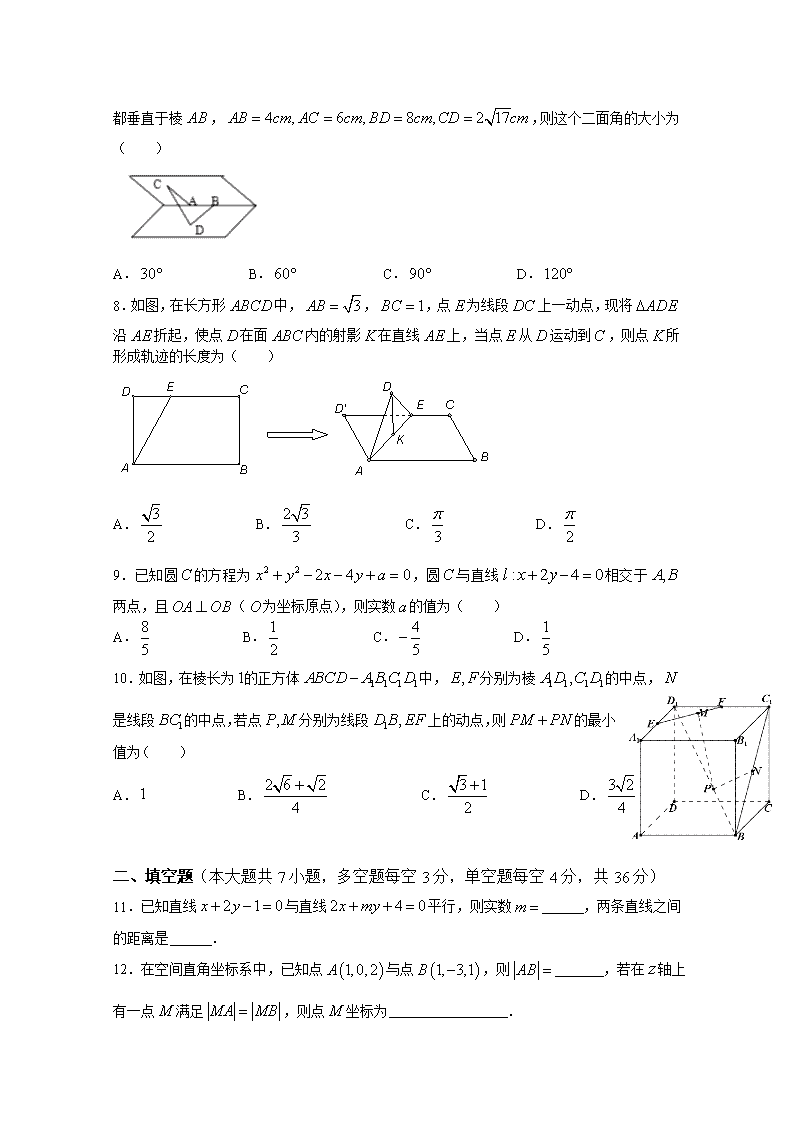
‎2018-2019学年浙江省慈溪市六校高二上学期期中考试数学试卷 一、选择题（本大题共10小题，每小题4分，共40分）‎ ‎1．直线的倾斜角为（ ）‎ A． B． C． D．‎ ‎2．若直线过第一、三、四象限，则实数满足（ ）‎ A． B． C． D．‎ ‎3．点在圆的内部，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎4．设是两条不同的直线，是两个不同的平面，则下列说法正确的是（ ）‎ A．若，则 B．若，则 C．若，则 D．若，则 ‎5．已知直线过点，且在轴和轴上的截距相等，则直线的方程为（ ）‎ A．‎ B．或 C．或 D．或或 ‎6．已知不等式组表示的平面区域为，若函数的图象上存在区域内的点，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎7．如图，在二面角的棱上有两个点，线段 分别在二面角的两个半平面内，并且都垂直于棱，，则这个二面角的大小为（ ）‎ A． B． C． D．‎ ‎8．如图，在长方形中，，，点为线段上一动点，现将沿折起，使点在面内的射影在直线上，当点从运动到，则点所形成轨迹的长度为（ ）‎ ‎ ‎ A． B． C． D．‎ ‎9．已知圆的方程为，圆与直线相交于两点，且（为坐标原点），则实数的值为（ ）‎ A． B． C． D．‎ ‎10．如图，在棱长为的正方体中，分别为棱的中点，是线段的中点，若点分别为线段上的动点，则的最小值为（ ）‎ A． B． C． D．‎ 二、填空题（本大题共7小题，多空题每空3分，单空题每空4分，共36分）‎ ‎11．已知直线与直线平行，则实数 ，两条直线之间的距离是 ．‎ ‎12．在空间直角坐标系中，已知点与点，则 ，若在轴上有一点满足，则点坐标为 ．‎ ‎13．过点的直线与圆交于,两点，当最小时，直线的方程为 ，此时 ．‎ ‎14．已知实数满足，目标函数的最大值是，则实数________，的最小值是________．‎ ‎15．已知实数满足，则的最小值为 ．‎ ‎16．已知点为圆外一点，若圆上存在一点，使得，则正数的取值范围是 ．‎ ‎17．在平面直角坐标系中，设为不同的两点，直线的方程为，设，其中均为实数．下列四个说法中：‎ ‎①存在实数，使点在直线上；‎ ‎②若，则过两点的直线与直线重合；‎ ‎③若，则直线经过线段的中点；‎ ‎④若，则点在直线的同侧，且直线与线段的延长线相交．‎ 所有结论正确的说法的序号是 ．‎ 三、解答题（本大题共5小题，第18题14分，第19至22题每题15分，共74分）‎ ‎18．已知的顶点，边上的中线所在直线为．‎ ‎（1）求直线的方程；‎ ‎（2）求点关于直线的对称点的坐标．‎ ‎19．如图，在四棱锥中，，，，，分别为线段的中点，平面．‎ ‎（1）求证：平面平面；‎ ‎（2）是否存在线段上一点，使得平面，若存在，求 的值；若不存在，请说明理由．‎ ‎20．如图，平面分别平行于，点分别在上，且，与所成的角的大小为．‎ ‎（1）求证：四边形是平行四边形；‎ ‎（2）点在的什么位置时，四边形的面积最大，最大值是多少？‎ ‎21．已知的三个顶点，其外接圆为圆．‎ ‎（1）若直线过点，且被圆截得的弦长为，求直线的方程；‎ ‎（2）对于线段（包括端点）上的任意一点，若在以为圆心的圆上都存在不同的两点，使得点是线段的中点，求圆的半径的取值范围．‎ ‎22．已知圆，点是直线上的一动点，过点作圆的切线，切点为．‎ ‎（1）当切线的长度为时，求点的坐标；‎ ‎（2）若的外接圆为圆，试问：当点在直线上运动时，圆是否过定点？若存在，求出所有的定点的坐标；若不存在，请说明理由；‎ ‎（3）求线段长度的最小值．‎ ‎2018学年第一学期高二期中六校联考数学参考答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 D C D D B A B C A D 二、填空题 ‎11． 12． 13． 14． 15． 16． 17．③④‎ 三、解答题 ‎18．解：（1）设边的中点为，则，边上的中线所在直线为，即为，故直线的方程为． …………7分 ‎（2）设点关于直线的对称点，则有 ‎，解得，即，所以点关于直线的对称点的坐标为．……14分 ‎19．解：（1）连结MO并延长交AB于E，设AC，BM的交点为F．‎ ‎，O是CD，AC的中点，，，‎ 是AB的中点，．‎ ‎．‎ ‎．‎ ‎，，‎ ‎≌，‎ ‎，．‎ ‎，．‎ ‎，，即．‎ 平面ABCD，平面ABCD，‎ ‎，又平面PAC，平面PAC，，‎ 平面PAC，又平面PBM，‎ 平面． …………8分 ‎（2）当N为线段PM上靠近点P的三等分点，即时，平面PAB．‎ 证明：连结PE，由（1）可知，，‎ ‎，‎ ‎，又平面PAB，平面PAB，‎ 平面PAB． …………15分 ‎20．解：（1）∵ 平面，平面，平面平面 ‎∴，同理 ‎∴，同理 ‎∴四边形为平行四边形． …………6分 ‎（2）由（1）可知在中，.‎ 记，则.‎ 在中，，则.∴‎ ‎∵，‎ ‎∴（或其补角）为与所成的角，故或 ‎∴，当且仅当，即时等号成立，故当为线段的中点时，四边形的面积最大，最大值为． …………15分 ‎21．解：（1）线段的垂直平分线方程为，线段的垂直平分线方程为，‎ 所以外接圆圆心，半径，‎ 圆的方程为．‎ 设圆心到直线的距离为，因为直线被圆截得的弦长为2，所以．‎ 当直线垂直于轴时，显然符合题意，即为所求；‎ 当直线不垂直于轴时，设直线方程为，则 ‎，解得，‎ 综上，直线的方程为或． …………6分 ‎（2）解法一：直线的方程为，设，‎ 因为点是线段的中点，所以，又都在半径为的圆上，‎ 所以即 因为该关于的方程组有解，即以为圆心，为半径的圆与以为圆心，为半径的圆有公共点，所以,‎ 又，所以对成立．‎ 而在[0,1]上的值域为[,10]，所以且．‎ 又点在圆外，所以对成立，即．故圆 的半径的取值范围为． …………15分 解法二：过点作交弦于点，则点为弦的中点．设，则有，．‎ 由勾股定理知，整理可得，所以对恒成立．‎ 令，由，可得，所以且，又，所以圆的半径的取值范围是． …………15分 ‎22．解：（1）由题意知，圆M的半径，设，‎ ‎∵PA是圆M的一条切线，∴，‎ ‎∴，解得，‎ ‎∴或． …………4分 ‎（2）设，∵，∴经过A，P，M三点的圆N以MP为直径，‎ 其方程为，‎ ‎（也可由圆的直径式方程，得圆的方程为）‎ 即，‎ 由，解得或，∴圆过定点，． …………9分 ‎（3）因为圆N方程为，‎ 即，圆M：，即，‎ ‎②-①得：圆M方程与圆N公共弦AB所在的直线方程为：，‎ 点M到直线AB的距离，‎ 相交弦长，‎ 当时，有最小值． …………15分