- 464.00 KB
- 2021-04-16 发布
2011中考数学压轴题思路训练(2011、5、9 )
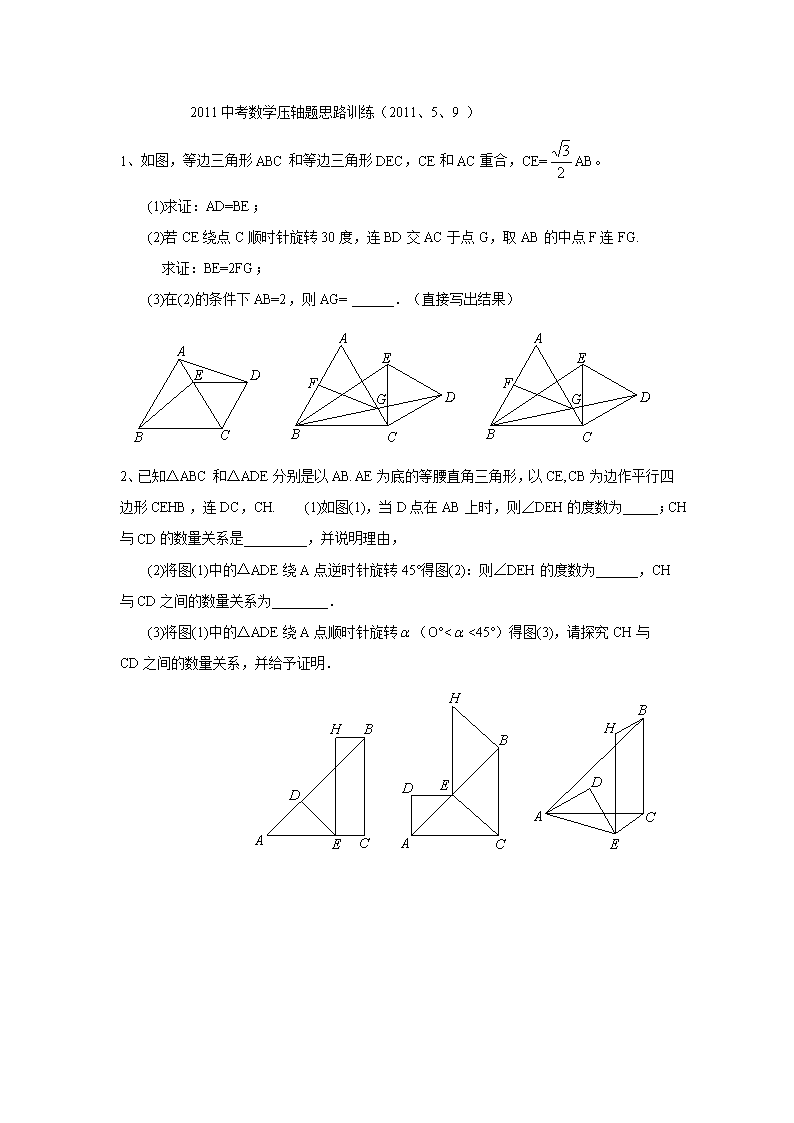
1、如图,等边三角形ABC和等边三角形DEC,CE和AC重合,CE=AB。
(1)求证:AD=BE;
(2)若CE绕点C顺时针旋转30度,连BD交AC于点G,取AB的中点F连FG.
求证:BE=2FG;
(3)在(2)的条件下AB=2,则AG= ______.(直接写出结果)
2、已知△ABC和△ADE分别是以AB.AE为底的等腰直角三角形,以CE,CB为边作平行四边形CEHB,连DC,CH. (1)如图(1),当D点在AB上时,则∠DEH的度数为_____;CH与CD的数量关系是_________,并说明理由,
(2)将图(1)中的△ADE绕A点逆时针旋转45°得图(2):则∠DEH的度数为______,CH
与CD之间的数量关系为________.
(3)将图(1)中的△ADE绕A点顺时针旋转(O°<<45°)得图(3),请探究CH与
CD之间的数量关系,并给予证明.
3、
4、
5、
6、C
B
A
O
y
x
(图10)
如图10,已知抛物线与轴负半轴交于点,与轴正半轴交于点,且.
(1) 求的值;
(2) 若点在抛物线上,且四边形是
平行四边形,试求抛物线的解析式;
(3) 在(2)的条件下,作∠OBC的角平分线,
与抛物线交于点P,求点P的坐标.
7、如图,二次函数与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
1、 求直线AC的解析式;
2、 设△PQC的面积为S,求S关于t的函数解析式;
3、 在y轴上找一点M,使△MAC和△MBC都是等腰三角形。直接写出所有满足条件的M点的坐标;
E
G
Q
P
O
y
x
C
B
A
4、 过点P作PE⊥AC,垂足为E,当P点运动时,线段EG的长度是否发生改变,请说明理由。
24.解:(1)由题意得:点B的坐标为,其中, (1分)
∵,点在轴的负半轴上,∴点的坐标为 (1分)
∵点在抛物线上,∴ (1分)
∴ (因为) (1分)
(2)∵四边形是平行四边形
∴,又∥轴,点B的坐标为
∴点的坐标为 (1分)
又点在抛物线上,
∴ ∴或(舍去) (1分)
又 由(1)知:
∴,. 抛物线的解析式为. (2分)
(3)过点作轴,,垂足分别为、
∵ 平分 ∴ (1分)
设点的坐标为
∴ (1分)
解得:或(舍去) (1分)
所以,点的坐标为 (1分)
相关文档
- 2020年区“十三五”服务业工作总结2021-04-16 21:39:339页
- 2017届高考数学(文)(新课标)二轮专题复2021-04-16 21:39:188页
- 北师大版数学六年级下册32021-04-16 21:39:1415页
- 山东高考数学理科真题word修改版2021-04-16 21:39:134页
- 六年级数学下册课件-3 圆柱的表面2021-04-16 21:39:0840页
- 【数学】2019届文科一轮复习人教A2021-04-16 21:38:5410页
- 数学(文)卷·2017届江苏省淮安市淮海2021-04-16 21:38:508页
- 中考英语形容词和副词考点归纳与例2021-04-16 21:38:447页
- 中考生物一轮复习生物的生殖和发育2021-04-16 21:38:445页
- 庙头中学中考物理训练题NO2021-04-16 21:38:443页