2018-2019学年湖北省武汉市华中师范大学第一附属中学高二下学期期中考试数学（理）试题 Word版 11页

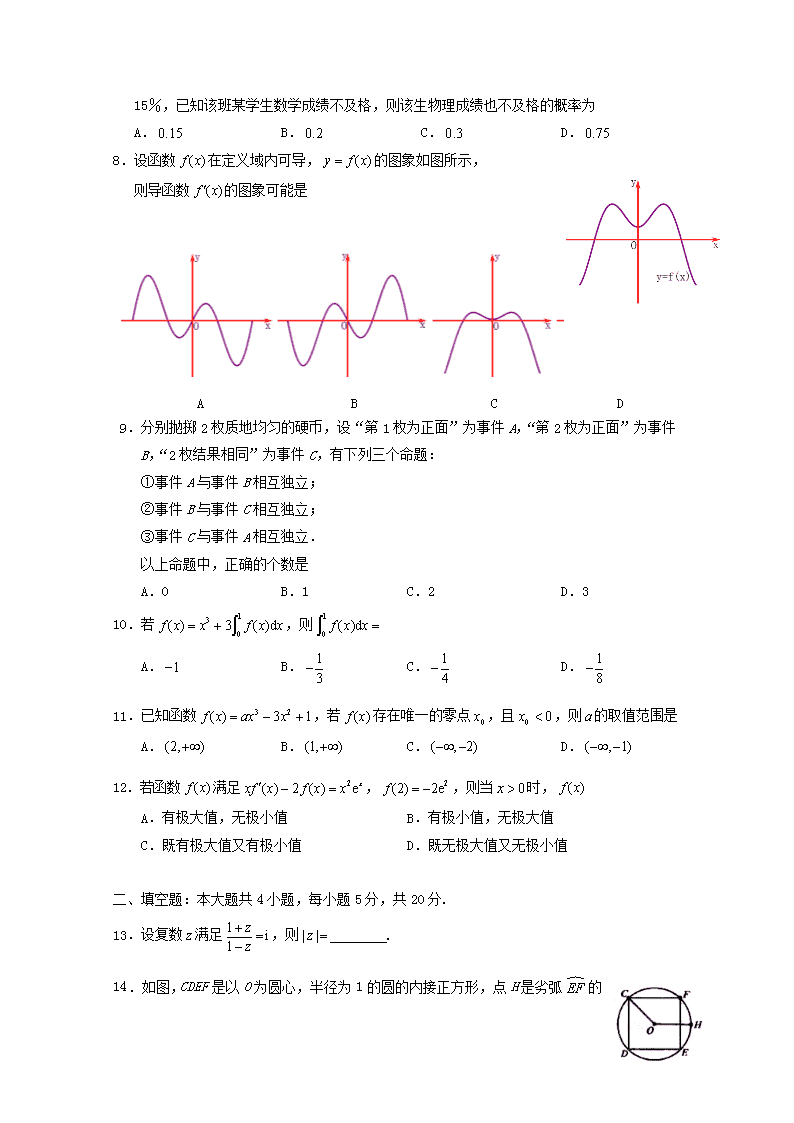
华中师大一附中2018—2019学年度下学期期中检测 高二年级理科数学试题 时限：120分钟 满分：150分 一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．若为虚数单位，复数，则表示复数的点在 ‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2．一物体的运动方程是为常数)，则该物体在时的瞬时速度是 A． B． C． D．‎ ‎3．曲线在点（0,1）处的切线斜率是 A． B．1 C．2 D．‎ ‎4．已知三个正态分布密度函数（，）的图象如图所示，则 A．，‎ B．，‎ C．，‎ D．，‎ ‎5．设，随机变量的分布列是 ‎0‎ ‎1‎ ‎2‎ ‎ 则当在内增大时， ‎ A．增大 B．减小 C．先增大，后减小 D．先减小，后增大 ‎6．设，，，…，，，则 ‎ A． B． C． D．‎ ‎7．一次考试中，某班级数学成绩不及格的学生占20％，数学成绩和物理成绩都不及格的学生占 ‎15％，已知该班某学生数学成绩不及格，则该生物理成绩也不及格的概率为 A． B． C． D．‎ ‎8．设函数在定义域内可导，的图象如图所示，‎ 则导函数的图象可能是 A B C D ‎9．分别抛掷2枚质地均匀的硬币，设“第1枚为正面”为事件A，“第2枚为正面”为事件B，“2枚结果相同”为事件C，有下列三个命题：‎ ‎ ①事件A与事件B相互独立；‎ ‎②事件B与事件C相互独立；‎ ‎③事件C与事件A相互独立．‎ 以上命题中，正确的个数是 A．0 B．1 C．2 D．3‎ ‎10．若，则 A． B． C． D．‎ ‎11．已知函数，若存在唯一的零点，且，则的取值范围是 A． B． C． D．‎ ‎12．若函数满足，，则当时，‎ A．有极大值，无极小值 B．有极小值，无极大值 ‎ C．既有极大值又有极小值 D．既无极大值又无极小值 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13．设复数满足，则 .‎ ‎14．如图，CDEF是以O为圆心，半径为1的圆的内接正方形，点H是劣弧 的中点，将一颗豆子随机地扔到圆O内，用A表示事件“豆子落在扇形OCFH内”，B表示事件“豆子落在正方形CDEF内”，则 .‎ ‎15．某一部件由四个电子元件按如图方式连接而成，元件1或元件2正常工作，且元件3或元件4正常工作，则部件正常工作.设四个电子元件的使用寿命（单位：小时）均服从正态分布，且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为 .‎ ‎16．传说中孙悟空的“如意金箍棒”是由“定海神针”变形得来的.定海神针在变形时永远保持为圆柱体，其底面半径原为12且以每秒1的等速率缩短，而长度以每秒20的等速率增长.已知神针之底面半径只能从12缩到4为止，且知在这段变形过程中，当底面半径为10时其体积最大.假设孙悟空将神针体积最小时定形成金箍棒，则此时金箍棒的底面半径为 .‎ 三、解答题：本大题共6小题，共70分. 解答应写出文字说明、证明过程或演算步骤.‎ ‎17．（10分）已知，a，b为实数．‎ ‎ （1）若，求；‎ ‎ （2）若，求a，b的值．‎ ‎18．（12分）袋中有20个大小相同的球，其中标号为0的有10个，标号为n的有n个（n =1,2,3,4）.现从袋中任取一球，X表示所取球的标号.求X的分布列、数学期望和方差.‎ ‎19．（12分）已知，R．求的单调增区间.‎ ‎20．（12分）Monte-Carlo方法在解决数学问题中有广泛的应用．下面利用Monte-Carlo 方法来估算定积分．考虑到等于由曲线，轴，直线所围成的区域的面积，如图，在外作一个边长为1正方形OABC．在正方形OABC内随机投掷n个点，若n个点中有m个点落入M中，则M的面积的估计值为，此即为定积分的估计值．现向正方形OABC中随机投掷10000个点，以X表示落入M中的点的数目．‎ ‎（1）求X的期望和方差；‎ ‎（2）求用以上方法估算定积分时，的估计值与 实际值之差在区间（-0.01，0.01）的概率．‎ ‎ ‎ ‎1899‎ ‎1900‎ ‎1901‎ ‎2099‎ ‎2100‎ ‎2101‎ ‎0.0058‎ ‎0.0062‎ ‎0.0067‎ ‎0.9933‎ ‎0.9938‎ ‎0.9942‎ ‎21．（12分）已知函数.‎ ‎（1）求的解析式；‎ ‎（2）若，求的最小值．‎ ‎22．（12分）‎ 已知函数，曲线在处的切线方程为.（为自然对数的底数，，e0.495≈1.640，e-0.703≈0.495）‎ ‎（1）求，的值；‎ ‎（2）证明：.‎ 华中师大一附中2018—2019学年度下学期期中检测 高二理科数学参考答案 一、选择题：本大题共12小题，每小题5分，共60分.‎ ‎1－5.DCCBB 6－10.CDADD 11－12.AB 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13．1 14． 15. 16.4‎ 三、解答题：本大题共6小题，共70分.‎ ‎17．(1)，所以………………………………………………………5分 ‎(2)由条件，得，所以 所以，解得……………………………………………………………………………5分 ‎18．X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎……………………………………………………………………………………………………………………4分 ‎∴……………………………………………………4分 ‎∴‎ ‎……………………………………………………………………………………………………………………4分 ‎19．的定义域为，…………………………………2分 当时，若，则，单调递增…………………………………………………2分 当时，‎ ‎(i)当时，‎ 当或时，，单调递增………………………………………2分 ‎(ii)当时，，在上，，单调递增……………………………………2分 ‎(iii)当时，‎ 当或时，，单调递增………………………………………2分 综上所述，当时，在上单调递增 当时，在，上单调递增 当时，在上单调递增 当时，在，上单调递增……………………………………………………2分 ‎20．(1)依题意，每个点落入中的概率为，‎ 所以，‎ ‎……………………………6分 ‎(2)依题意，所求概率为 ‎………………………………………………………………………………………………………………………12分 ‎21．(1)由已知得，‎ 从而，‎ 于是 由于，故当时，；当时，；当时，‎ 从而的单调增区间为和 单调减区间为……………………………………………………………………………………6分 ‎(2)由已知条件得 设，则 ‎①若，则，无最大值 ‎②若，则当时，；当时，‎ 从而在上单调递增，在上单调递减 故有最大值 所以等价于 因此 设，则 当时，；当时，‎ 所以在上单调递减，在上单调递增 故有最小值 从而 当且仅当即时，的最小值为……………………………………………………………………………………………………12分 ‎22.(1)函数的定义域为，‎ 由题意可得,‎ 故，………………………………………………………………………………………………4分 ‎(2)解法一：由(1)知，，从而等价于 设函数，则 所以当时，；当时，‎ 故在单调递减，在单调递增，从而在的最小值为 设函数，则 所以当时，；当时，‎ 故在单调递增，在单调递减，从而在的最大值为 因为，所以，从而 综上，当时，，即…………………………………………………………12分 ‎………………………………………………………………………………………………………………………１２分