2018届二轮复习圆周运动课件（58张）全国通用 58页

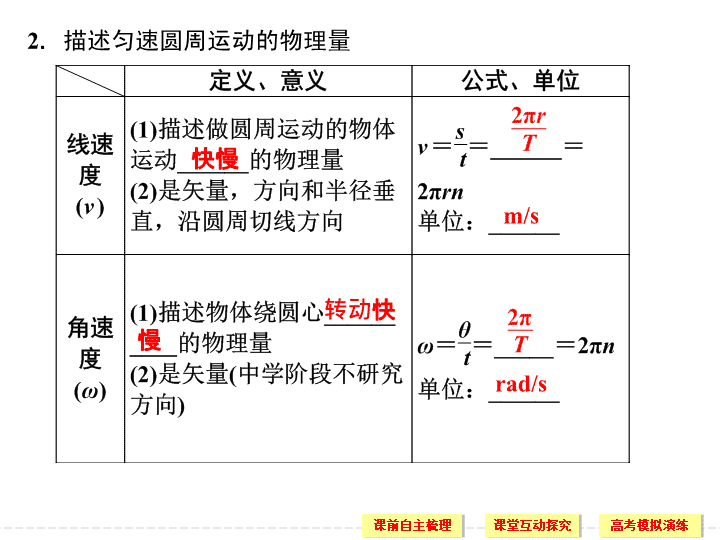
基础课 3 　圆周运动 知识点一、匀速圆周运动、角速度、线速度、向心加速度 1 ． 匀速圆周运动 (1) 定义：在任意相等时间内通过的弧长都 _______ 的圆周运动叫做匀速圆周运动。 (2) 特点：加速度大小 ______ ，方向始终指向 ______ ，是变加速运动。 (3) 条件：合外力大小 ______ 、方向始终与 ______ 方向垂直且指向圆心。 不变 圆心 不变 速度 相等 2 ． 描述匀速圆周运动的物理量 m/s rad/s 快慢 转动快 慢 一圈 方向 圆心 s ω 2 r m/s 2 方向 大小 圆心 合力 分力 mω 2 r 知识点三、离心 运动 1 ． 定义： 做 __________ 的物体，在 受到的 合外力突然消失或不足以提供圆周运动所需 要的 ________ 的情况下， 将 远离圆心运动 ，我们把这种运动称为离心运动 。 2 ． 本质： 做圆周运动的物体，由于本身的惯性，总有沿着圆周 ___________ 飞出去的趋势。 圆周运动 向心力 切线方向 3 ． 受力特点 (1) 当 F ＝ ______ 时，物体做匀速圆周运动； (2) 当 F ＝ 0 时，物体沿 _____ 方向飞出； (3) 当 F ＜ ______ 时，物体逐渐远离圆心， F 为实际提供的向心力，如图 1 所示。 图 1 mω 2 r 切线 mω 2 r [ 思考判断 ] (1) 匀速圆周运动是匀变速曲线运动。 ( 　　 ) (2) 匀速圆周运动加速度恒定不变。 ( 　　 ) (3) 做匀速圆周运动的物体所受合外力大小保持不变。 ( 　　 ) (4) 比较物体沿圆周运动的快慢看线速度，比较物体绕圆心转动的快慢看周期或角速度 ( 　　 ) (5) 随水平圆盘一起匀速转动的物体 A 受重力、支持力和向心力作用。 ( 　　 ) (6) 做圆周运动的物体所受合外力突然消失，物体将沿圆周的半径方向飞出。 ( 　　 ) (7) 汽车转弯时速度过大就会向外发生侧滑，这是汽车轮胎受沿转弯半径向内的静摩擦力不足以提供汽车转弯所需向心力的缘故。 ( 　　 ) 答案　 (1) × 　 (2) × 　 (3) √ 　 (4) √ 　 (5) × 　 (6) × 　 (7) √ 圆周运动的运动学问题 1 ． 对公式 v ＝ ωr 的进一步理解 (1) 当 r 一定时， v 与 ω 成正比。如齿轮边缘处的质点随着齿轮转速的增大，角速度和线速度都增大。 (2) 当 ω 一定时， v 与 r 成正比。如地球上各点都绕地轴做圆周运动，角速度相同，地球表面纬度越低的地方，到地轴的距离越大，线速度越大。 (3) 当 v 一定时， ω 与 r 成反比。如皮带传运动装置中，两轮边缘上各点的线速度大小相等，大轮的半径 r 大，角速度 ω 较小。 图 2 A ． A 点与 C 点的角速度大小相等 B ． A 点与 C 点的线速度大小相等 C ． B 点与 C 点的角速度大小之比为 2 ∶ 1 D ． B 点与 C 点的向心加速度大小之比为 1 ∶ 4 答案　 BD 2 ． [ 摩擦传动 ] 如图 3 所示， B 和 C 是一组塔轮，即 B 和 C 半径不同，但固定在同一转动轴上，其半径之比为 R B ∶ R C ＝ 3 ∶ 2 ， A 轮的半径大小与 C 轮相同，它与 B 轮紧靠在一起，当 A 轮绕过其中心的竖直轴转动时，由于摩擦作用， B 轮也随之无滑动地转动起来。 a 、 b 、 c 分别为三轮边缘的三个点，则 a 、 b 、 c 三点在转动过程中的 ( 　　 ) 图 3 A ．线速度大小之比为 3 ∶ 2 ∶ 2 B ．角速度之比为 3 ∶ 3 ∶ 2 C ．转速之比为 2 ∶ 3 ∶ 2 D ．向心加速度大小之比为 9 ∶ 6 ∶ 4 答案　 D 3 ． [ 与生产相结合 ] 某机器内有两个围绕各自的固定轴匀速转动的铝盘 A 、 B 。 A 盘固定一个信号发射装置 P ，能持续沿半径向外发射红外线， P 到圆心的距离为 28 cm 。 B 盘上固定一个带窗口的红外线信号接收装置 Q ， Q 到圆心的距离为 16 cm 。 P 、 Q 转动的线速度相同，都是 4π m/s 。当 P 、 Q 正对时， P 发出的红外线恰好进入 Q 的接收窗口，如图 4 所示，则 Q 每隔一定时间就能接收到红外线信号，这个时间的最小值应为 ( 　　 ) 图 4 A ． 0.56 s B ． 0.28 s C ． 0.16 s D ． 0.07 s 解析　 根据公式 T ＝ 可求出 P 、 Q 转动的周期分别为 T 1 ＝ 0.14 s 和 T 2 ＝ 0.08 s 。根据题意，只有当 P 、 Q 同时转到题图所示位置时， Q 才能接收到红外线信号，所以所求的最小时间应该是它们转动周期的最小公倍数，即 0.56 s ，所以 A 正确。 答案　 A 常见的三种传动方式及特点 (1) 同轴传动： 如图甲、乙所示，绕同一转轴转动的物体，角速度相同， ω A ＝ ω B ，由 v ＝ ωr 知 v 与 r 成正比。 反思总结 (2) 皮带传动： 如图甲、乙所示，皮带与两轮之间无相对滑动时，两轮边缘线速度大小相等，即 v A ＝ v B 。 (3) 摩擦传动： 如图所示，两轮边缘接触，接触点无打滑现象时，两轮边缘线速度大小相等，即 v A ＝ v B 。 圆周运动中的动力学问题 1 ． 向心力的来源 (1) 向心力的方向沿半径指向圆心； (2) 向心力来源：一个力或几个力的合力或某个力的分力。 2 ． 向心力的确定 (1) 确定圆周运动的轨道所在的平面，确定圆心的位置。 (2) 分析物体的受力情况，找出所有的力沿半径方向指向圆心的合力就是向心力。 1 ． [ 对向心力表达式的理解 ] 某同学为感受向心力的大小与哪些因素有关，做了一个小实验：绳的一端拴一小球，手牵着在空中甩动，使小球在水平面内做圆周运动 ( 如图 5 所示 ) ，则下列说法中正确的是 ( 　　 ) 图 5 A ．保持绳长不变，增大角速度，绳对手的拉力将不变 B ．保持绳长不变，增大角速度，绳对手的拉力将增大 C ．保持角速度不变，增大绳长，绳对手的拉力将不变 D ．保持角速度不变，增大绳长，绳对手的拉力将减小 答案　 B A ． 15 m/s B ． 20 m/s C ． 25 m/s D ． 30 m/s 答案　 B 图 6 答案　 C “ 一、二、三、四 ” 求解圆周运动问题 方法技巧 圆周运动中的临界问题 1 ． 水平面内圆周运动的临界问题 关于水平面内的匀速圆周运动的临界问题，主要是临界速度和临界力的问题。常见的是与绳的拉力、弹簧的拉力、接触面的弹力和摩擦力等相关的问题。通过受力分析来确定临界状态和临界条件，是较常用的解题方法。 2 ． 竖直平面内圆周运动的临界问题 (1) “ 轻绳 ” 模型和 “ 轻杆 ” 模型不同的原因在于 “ 轻绳 ” 只能对小球产生拉力，而 “ 轻杆 ” 既可对小球产生拉力也可对小球产生支持力。 (2) 有关临界问题出现在变速圆周运动中，竖直平面内的圆周运动是典型的变速圆周运动，一般情况下，只讨论最高点和最低点的情况。 物理情景 最高点无支撑 最高点有支撑 实例 球与绳连接、水流星、沿内轨道的 “ 过山车 ” 等 球与杆连接、球在光滑管道中运动等 图示 受力 特征 除重力外，物体受到的弹力方向：向下或等于零 除重力外，物体受到的弹力方向：向下、等于零或向上 【 典例 】 长 L ＝ 0.5 m 质量可忽略的细杆，其一端可绕 O 点在竖直平面内转动，另一端固定着一个小球 A 。 A 的质量为 m ＝ 2 kg ，当 A 通过最高点时，如图 7 所示，求在下列两种情况下杆对小球的作用力： 图 7 答案　 (1)16 N 　方向向上　 (2)44 N 　方向向下 【拓展延伸】 在 【典例】 中若把细杆换成细绳，则在 (1)(2) 两种情况下小球能否过最高点？若能，此时细绳对小球的拉力为多大？ 分析竖直平面内圆周运动临界问题的思路 建模指导 1 ． [ “ 轻绳 ” 模型 ] ( 多选 ) 如图 8 所示，竖直环 A 半径为 r ，固定在木板 B 上，木板 B 放在水平地面上， B 的左右两侧各有一挡板固定在地上， B 不能左右运动，在环的最低点静放有一小球 C ， A 、 B 、 C 的质量均为 m 。现给小球一水平向右的瞬时速度 v ，小球会在环内侧做圆周运动，为保证小球能通过环的最高点，且不会使环在竖直方向上跳起 ( 不计小球与环的摩擦阻力 ) ，瞬时速度必须满足 ( 　　 ) 图 8 答案　 CD 2 ． [ 水平面内与摩擦力有关的临界问题 ] ( 多选 ) 如图 9 所示， A 、 B 、 C 三个物体放在旋转圆台上，动摩擦因数均为 μ ， A 的质量为 2 m ， B 、 C 的质量均为 m ， A 、 B 离轴的距离为 R ， C 离轴的距离为 2 R ，则当圆台旋转时 ( 设 A 、 B 、 C 都没有滑动 )( 　　 ) 图 9 A ． C 的向心加速度最大 B ． B 的静摩擦力最小 C ．当圆台转速增大时， A 比 B 先滑动 D ．当圆台转速增大时， C 将最先滑动 答案　 ABD 3 ． [ 水平面内与弹力有关的临界问题 ] 如图 10 所示， AB 为竖直转轴，细绳 AC 和 BC 的结点 C 系一质量为 m 的小球，两绳能承受的最大拉力均为 2 mg 。当 AC 和 BC 均拉直时 ∠ ABC ＝ 90° ， ∠ ACB ＝ 53° ， BC ＝ 1 m 。 ABC 能绕竖直轴 AB 匀速转动，因而 C 球在水平面内做匀速圆周运动。当小球的线速度增大时，两绳均会被拉断，则最先被拉断的那根绳及另一根绳被拉断时的速度分别为 ( g 取 10 m/s 2 )( 　　 ) A ． AC 　 5 m/s B ． BC 　 5 m/s C ． AC 　 5.24 m/s D ． BC 　 5.24 m/s 图 10 答案 　 B 解决临界问题的一般思路 首先要考虑达到临界条件时物体所处的状态，其次分析该状态下物体的受力特点，最后结合圆周运动知识，列出相应的动力学方程综合分析。 反思总结 1 ． (2016· 全国卷 Ⅱ ， 16) 小球 P 和 Q 用不可伸长的轻绳悬挂在天花板上， P 球的质量大于 Q 球的质量，悬挂 P 球的绳比悬挂 Q 球的绳短。将两球拉起，使两绳均被水平拉直，如图 11 所示。将两球由静止释放。在各自轨迹的最低点 ( 　　 ) 图 11 A ． P 球的速度一定大于 Q 球的速度 B ． P 球的动能一定小于 Q 球的动能 C ． P 球所受绳的拉力一定大于 Q 球所受绳的拉力 D ． P 球的向心加速度一定小于 Q 球的向心加速度 答案　 C 2. (2014· 全国卷 Ⅱ ， 17) 如图 12 ，一质量为 M 的光滑大圆环，用一细轻杆固定在竖直平面内；套在大环上质量为 m 的小环 ( 可视为质点 ) ，从大环的最高处由静止滑下。重力加速度大小为 g 。当小环滑到大环的最低点时，大环对轻杆拉力的大小为 ( 　　 ) 图 12 A ． Mg － 5 mg B ． Mg ＋ mg C ． Mg ＋ 5 mg D ． Mg ＋ 10 mg 答案　 C 3 ． (2014· 全国卷 Ⅰ ， 20) ( 多选 ) 如图 13 ，两个质量均为 m 的小木块 a 和 b ( 可视为质点 ) 放在水平圆盘上， a 与转轴 OO ′ 的距离为 l ， b 与转轴的距离为 2 l ，木块与圆盘的最大静摩擦力为木块所受重力的 k 倍，重力加速度大小为 g 。若圆盘从静止开始绕转轴缓慢地加速转动，用 ω 表示圆盘转动的角速度，下列说法正确的是 ( 　　 ) 图 13 答案　 AC 4 ． (2016· 福建漳州三联 ) 两根长度不同的细线下面分别悬挂两个小球，细线上端固定在同一点，若两个小球以相同的角速度，绕共同的竖直轴在水平面内做匀速圆周运动，则两个摆球在运动过程中，相对位置关系示意图正确的是 ( 　　 ) 答案　 B