- 261.50 KB
- 2021-04-16 发布
2018年四川省达州市高考数学一诊试卷(文科)
一、选择题(每小题5分,共60分,每小题四个选项中只有一个是符合题意的,请将正确答案番号按要求涂在答题卡上相应位置)
1.(5分)复数1+2i在复平面内所对应的点在( )
A.第一象限 B.第二象限{ C.第三象限 D.第四象限
2.(5分)已知集合A={x|1≤x≤3},B={x|﹣5<x≤3},则A∩B=( )
A.{x|﹣3<x≤1} B.{x|﹣1<x≤3}}{} C.{x|﹣1≤x≤3} D.{x|1≤x≤3}
3.(5分)某8人一次比赛得分茎叶图如图所示,这组数据的中位数和众数分别是( )
A.85 和 92 B.87 和 92 C.84 和 92 D.85 和 90
4.(5分)在等比数列{an}中,a3=2,a6=16,则数列{an}的公比是( )
A.﹣2 B. C.2 D.4
5.(5分)已知sinα=,则cos(π+2α)=( )
A.﹣- B.- C.﹣ D.
6.(5分)函数f(x)=sin(x﹣),则f(x)的图象的对称轴方程为( )
A.x=+kπ,k∈Z B.x=+2kπ,k∈Z
C.x=﹣+2kπ,k∈Z D.x=+kπ,k∈Z
7.(5分)以圆x2+y2=4与x轴的交点为焦点,以抛物线y2=10x的焦点为一个顶点且中心在原点的椭圆的离心率是( )
A. B. C. D.
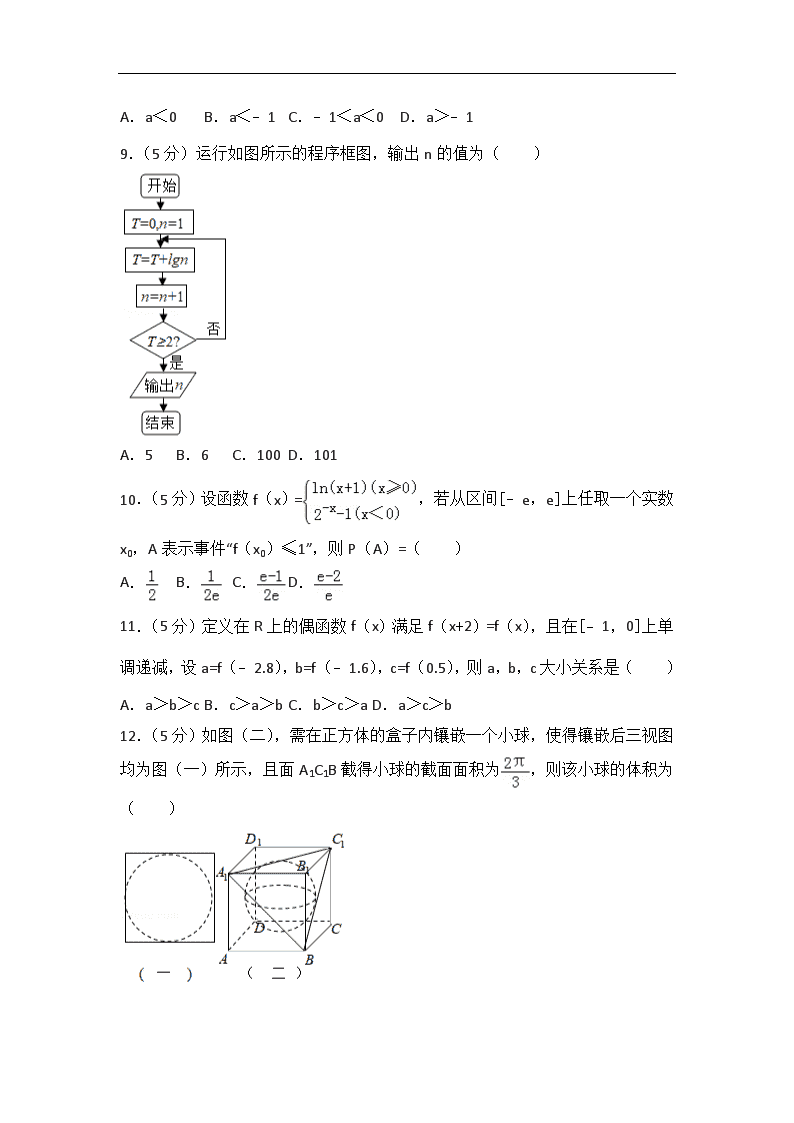
8.(5分)方程x2﹣2x+a+1=0有一正一负两实根的充要条件是( )
A.a<0 B.a<﹣1 C.﹣1<a<0 D.a>﹣1
9.(5分)运行如图所示的程序框图,输出n的值为( )
A.5 B.6 C.100 D.101
10.(5分)设函数f(x)=,若从区间[﹣e,e]上任取一个实数x0,A表示事件“f(x0)≤1”,则P(A)=( )
A. B. C. D.
11.(5分)定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[﹣1,0]上单调递减,设a=f(﹣2.8),b=f(﹣1.6),c=f(0.5),则a,b,c大小关系是( )
A.a>b>c B.c>a>b C.b>c>a D.a>c>b
12.(5分)如图(二),需在正方体的盒子内镶嵌一个小球,使得镶嵌后三视图均为图(一)所示,且面A1C1B截得小球的截面面积为,则该小球的体积为( )
A. B. C.p D.
二、填空题(每小题5分,共20分,请将答案填在答题卡上相应位置)
13.(5分)过点P(1,2),斜率为﹣3的直线的一般式方程为 .
14.(5分)向量=(λ,1),=(1,﹣2),若⊥,则λ的值为 .
15.(5分)已知x,y满足í,则2x﹣y的最大值是 .
16.(5分)若任意a,b满足0<a<b<t,都有blna<alnb,则t的最大值为 .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.
17.(12分)已知函数f(x)=sin(2x﹣).
(1)求函数f(x)的周期;
(2)在△ABC中,f(A)=1,且满足sin2B+sinA•sinC=sin2A+sin2C,求角C.
18.(12分)已知函数f(x)=ax 2+bx的图象经过(﹣1,0)点,且在x=﹣1处的切线斜率为﹣1,设数列{an}的前n项和Sn=f(n)(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{}前n项的和Tn.
19.(12分)某市去年外出务工返乡创业人员中有1000名个人年收入在区间[1,41](单位:万元)上,从这 1000
名中随机抽取100名,得到这100名年收入频率分布直方图.这些数据区间是[1,5],…,(37,41].
已接受职业技术教育
未接受职业技术教育
总计
个人年收入超过17万元
340
个人年收入不超过17万元
总计
600
1000
(1)用样本估计总体,试用直方图估算这1000名外出务工返乡创业人员年收入为(33,41]万元的人数;(2)调查发现这1000名返乡创业人员中有600人接受了职业技术教育,其中340人个人年收入超过17万元.请完成个人年收入与接受职业教育2×2列联表,是否有99%的把握认为该市这1000人返乡创业收入与创业人员是否接受职业技术教育有关?请说明理由.
参考公式及数据K2检验临界值表:
K2=(其中n=a+b+c+d)
P(K2≥k0)
0.05
0.025
0.010
0.005
0.001
k0
3.841
5.024
6.635
7.879
10.828
20.(12分)如图,在直三棱柱ABC﹣A1B1C1中,点M,N分别为线段A1B,B1C的中点.
(1)求证:MN∥平面AA1C1C;
(2)若∠ABC=90°,AB=BC=2,AA1=3,求点B1到面A1BC的距离.
21.(12分)已知函数f(x)=lnx﹣ax,g(x)=x2﹣(2a+1)x+(a+1)lnx.
(1)当a=1时,求函数f(x)的极大值;
(2)当a≥1时,求证:方程f(x)=g(x)有唯一实根.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.选修4-4参数方程与极坐标
22.(10分)在直角坐标系xOy中,以坐标原点O为极点,以x轴为极轴建立极坐标系.已知直线l:(t为参数),曲线C的极坐标方程是ρ2﹣6ρcosθ+1=0,l与C相交于两点A、B.
(1)求l的普通方程和C的直角坐标方程;
(2)已知M(0,﹣1),求|MA|•|MB|的值.
选修4-5不等式选讲
23.已知正数a,b,c满足:a+b+c=1,函数f(x)=|x﹣|+|x+|.
(1)求函数f(x)的最小值;
(2)求证:f(x)≥9.
2018年四川省达州市高考数学一诊试卷(文科)
参考答案与试题解析
一、选择题(每小题5分,共60分,每小题四个选项中只有一个是符合题意的,请将正确答案番号按要求涂在答题卡上相应位置)
1.(5分)复数1+2i在复平面内所对应的点在( )
A.第一象限 B.第二象限{ C.第三象限 D.第四象限
【解答】解:复数1+2i在复平面内所对应的点的坐标为(1,2)
所以:该点在第一象限.
故选:A.
2.(5分)已知集合A={x|1≤x≤3},B={x|﹣5<x≤3},则A∩B=( )
A.{x|﹣3<x≤1} B.{x|﹣1<x≤3}}{} C.{x|﹣1≤x≤3} D.{x|1≤x≤3}
【解答】解:∵集合A={x|1≤x≤3},B={x|﹣5<x≤3},
∴A∩B={x|1≤x≤3}.
故选:D.
3.(5分)某8人一次比赛得分茎叶图如图所示,这组数据的中位数和众数分别是( )
A.85 和 92 B.87 和 92 C.84 和 92 D.85 和 90
【解答】解:这组数据从小到大为:82,83,84,85,89,92,92,93,
众数为92,中位数为中间两数的平均数,即(85+89)÷2=87
故选:B
4.(5分)在等比数列{an}中,a3=2,a6=16,则数列{an}的公比是( )
A.﹣2 B. C.2 D.4
【解答】解:根据题意,等比数列{an}中,a3=2,a6=16,
则q3==8,
解可得q=2;
故选:C.
5.(5分)已知sinα=,则cos(π+2α)=( )
A.﹣- B.- C.﹣ D.
【解答】解:已知sinα=,
由cos(π+2α)=﹣cos2α=﹣(1﹣2sin2α)=2×=
故选:A.
6.(5分)函数f(x)=sin(x﹣),则f(x)的图象的对称轴方程为( )
A.x=+kπ,k∈Z B.x=+2kπ,k∈Z
C.x=﹣+2kπ,k∈Z D.x=+kπ,k∈Z
【解答】解:函数f(x)=sin(x﹣),
则f(x)的图象的对称轴方程:x﹣=+kπ,
可得:x=,k∈Z.
故选:A.
7.(5分)以圆x2+y2=4与x轴的交点为焦点,以抛物线y2=10x的焦点为一个顶点且中心在原点的椭圆的离心率是( )
A. B. C. D.
【解答】解:根据题意,x2+y2=4与x轴的交点为(±2,0),抛物线y2=10x的焦点为(,0),
即椭圆的焦点为(±2,0),椭圆的顶点为(,0),
则椭圆中c=2,a=,
则椭圆的离心率e===;
故选:C.
8.(5分)方程x2﹣2x+a+1=0有一正一负两实根的充要条件是( )
A.a<0 B.a<﹣1 C.﹣1<a<0 D.a>﹣1
【解答】解:∵方程x2﹣2x+a+1=0有一正一负两实根,
∴,
解得a<﹣1.
故选:B.
9.(5分)运行如图所示的程序框图,输出n的值为( )
A.5 B.6 C.100 D.101
【解答】解:第一次执行循环体后,T=0,n=2,不满足退出循环的条件;
第二次执行循环体后,T=lg2,n=3,不满足退出循环的条件;
第三次执行循环体后,T=lg6,n=4,不满足退出循环的条件;
第四 次执行循环体后,T=lg24,n=5,不满足退出循环的条件;
第五次执行循环体后,T=lg120,n=6,满足退出循环的条件;
故输出的n值为6,
故选:B
10.(5分)设函数f(x)=,若从区间[﹣e,e]上任取一个实数x0,A表示事件“f(x0)≤1”,则P(A)=( )
A. B. C. D.
【解答】解:∵函数f(x)=,x∈[﹣e,e],
解f(x0)≤1得:x0∈[﹣1,e﹣1]
故P(A)==,
故选:A
11.(5分)定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[﹣1,0]上单调递减,设a=f(﹣2.8),b=f(﹣1.6),c=f(0.5),则a,b,c大小关系是( )
A.a>b>c B.c>a>b C.b>c>a D.a>c>b
【解答】解:∵偶函数f(x)满足f(x+2)=f(x),∴函数的周期为2.
由于a=f(﹣2.8)=f(﹣0.8),
b=f(﹣1.6)=f(0.4)=f(﹣0.4),
c=f(0.5)=f(﹣0.5),
﹣0.8<﹣0.5<﹣0.4,且函数f(x)在[﹣1,0]上单调递减,
∴a>c>b,
故选:D
12.(5分)如图(二),需在正方体的盒子内镶嵌一个小球,使得镶嵌后三视图均为图(一)所示,且面A1C1B截得小球的截面面积为,则该小球的体积为( )
A. B. C.p D.
【解答】解:设正方体盒子的棱长为2a,则内接球的半径为a,
平面A1BC1是边长为2a的正三角形,
且球与以点B1为公共点的三个面的切点恰为△A1BC1三边的中点,
∴所求截面的面积是该正三角形的内切圆的面积,
则由图得,△A1BC1内切圆的半径是a×tan30°=a,
则所求的截面圆的面积是π×a×a=a2=a=1
∴该小球的体积为V球=•13=.
故选:B.
二、填空题(每小题5分,共20分,请将答案填在答题卡上相应位置)
13.(5分)过点P(1,2),斜率为﹣3的直线的一般式方程为 3x+y﹣5=0 .
【解答】解:由题意可得直线的点斜式方程为:y﹣2=﹣3(x﹣1),
化为一般式可得3x+y﹣5=0
故答案为:3x+y﹣5=0.
14.(5分)向量=(λ,1),=(1,﹣2),若⊥,则λ的值为 2 .
【解答】解:向量=(λ,1),=(1,﹣2),
若⊥,则•=λ﹣2=0,
解答λ=2.
故答案为:2.
15.(5分)已知x,y满足í,则2x﹣y的最大值是 4 .
【解答】解:根据x,y满足画出可行域,
如图:
由图得当z=2x﹣y过的交点A(2,0)时,
Z最大为4.
故答案为:4.
16.(5分)若任意a,b满足0<a<b<t,都有blna<alnb,则t的最大值为 e .
【解答】解:∵0<a<b<t,blna<alnb,
∴<,(a<b),
令y=,则函数在(0,t)递增,
故y′=>0,
解得:0<x<e,
故t的最大值是e,
故答案为:e.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.
17.(12分)已知函数f(x)=sin(2x﹣).
(1)求函数f(x)的周期;
(2)在△ABC中,f(A)=1,且满足sin2B+sinA•sinC=sin2A+sin2C,求角C.
【解答】解:函数f(x)=sin(2x﹣).
(1)函数f(x)的周期T=;
(2)由f(A)=1,即sin(2A﹣)=1,
∵0<A<π,
∴2A﹣=
可得:A=.
∵sin2B+sinA•sinC=sin2A+sin2C
正弦定理可得:ac=a2+c2
由余弦定理:cosB===.
∵0<B<π,
可得:B=.
那么:C=π﹣A﹣B=
18.(12分)已知函数f(x)=ax 2+bx的图象经过(﹣1,0)点,且在x=﹣1处的切线斜率为﹣1,设数列{an}的前n项和Sn=f(n)(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{}前n项的和Tn.
【解答】解:(1)函数f(x)=ax 2+bx的图象经过(﹣1,0)点,
则:a﹣b=0,
即a=b①,
由于:f′(x)=2ax+b,函数f(x)=ax 2+bx在x=﹣1处的切线斜率为﹣1,
则:﹣2a+b=﹣1②,
由①②得:a=1,b=1.
数列{an}的前n项和Sn=f(n)=n2+n,
,
所以:an=Sn﹣Sn﹣1=2n,
当n=1时,a1=2符合上式,
则:an=2n.
(2)由于an=2n,
则:==,
则:+…+,
=,
=.
19.(12分)某市去年外出务工返乡创业人员中有1000名个人年收入在区间[1,41](单位:万元)上,从这 1000
名中随机抽取100名,得到这100名年收入频率分布直方图.这些数据区间是[1,5],…,(37,41].
已接受职业技术教育
未接受职业技术教育
总计
个人年收入超过17万元
340
个人年收入不超过17万元
总计
600
1000
(1)用样本估计总体,试用直方图估算这1000名外出务工返乡创业人员年收入为(33,41]万元的人数;(2)调查发现这1000名返乡创业人员中有600人接受了职业技术教育,其中340人个人年收入超过17万元.请完成个人年收入与接受职业教育2×2列联表,是否有99%的把握认为该市这1000人返乡创业收入与创业人员是否接受职业技术教育有关?请说明理由.
参考公式及数据K2检验临界值表:
K2=(其中n=a+b+c+d)
P(K2≥k0)
0.05
0.025
0.010
0.005
0.001
k0
3.841
5.024
6.635
7.879
10.828
【解答】解:(1)收入在(33,41]上的返乡创业人员频率为
0.010×4+0.005×4=0.06,
估算这1000名外出务工返乡创业人员年收入为(33,41]万元的人数为
1000×0.06=60(人);
(2)根据题意,这1000名返乡创业人员中年收入超过 17 万元的人数是
1000×[1﹣(0.01+0.02+0.03+0.04)×4]=600,其中参加职业培训的人数是340人,
由此填写2×2列联表如下;
已接受职业技术教育
未接受职业技术教育
总计
个人年收入超过17万元
340
260
600
个人年收入不超过17万元
260
140
400
总计
600
400
1000
计算K2=≈6.944>6.635,
所以有99%的把握认为该市这 1000 人返乡创业收入与创业人员是否接受职业技术教育有关.
20.(12分)如图,在直三棱柱ABC﹣A1B1C1中,点M,N分别为线段A1B,B1C的中点.
(1)求证:MN∥平面AA1C1C;
(2)若∠ABC=90°,AB=BC=2,AA1=3,求点B1到面A1BC的距离.
【解答】(1)证明:连接BC1,
∵四边形BCC1B1是平行四边形,N是B1C的中点,
∴N是BC1的中点,又M是A1B的中点,
∴MN∥A1C1,
又A1C1⊂平面AA1C1C,MN⊄平面AA1C1C,
∴MN∥平面AA1C1C.
(2)解:∵AB⊥BC,BB1⊥BC,AB∩BB1=B,
∴BC⊥平面ABB1A1,
∴V=S•BC==2,
又A1B==,∴S==.
设B1到平面A1BC的距离的距离为h,则V=•h=,
∵V=V,∴2=,∴h=.
∴点B1到面A1BC的距离为.
21.(12分)已知函数f(x)=lnx﹣ax,g(x)=x2﹣(2a+1)x+(a+1)lnx.
(1)当a=1时,求函数f(x)的极大值;
(2)当a≥1时,求证:方程f(x)=g(x)有唯一实根.
【解答】解:(1)a=1时,函数f(x)=lnx﹣x,,
x∈(0,1)时,f′(x)>0,x∈(1,+∞)时,f′(x)<0,
∴f(x)在(0,1)递增,在(1,+∞)递减,
∴x=1时,函数f(x)取得极大值f(1)=﹣1.
(2)方程f(x)=g(x)的根⇔的根,
令h(x)=,(x>0,a≥1)
,
①当a=1时,h′(x)≥0在(0,+∞)恒成立,函数h(x)单调递增,方程f(x)=g(x)有唯一实根.
②当a>1时,x∈(0,1)时,h′(x)>0,x∈(1,a)时,′(x)<0,x∈(a,+∞)时,h′(x)>0,
∴h(x)在(0,1),(a,+∞)单调递增,在(1,a)单调递减,
而h(1)=﹣a﹣,x→+∞时,h(x)→+∞,
函数h(x)与x轴只有一个交点,∴方程f(x)=g(x)有唯一实根.
综上所述:方程f(x)=g(x)有唯一实根.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.选修4-4参数方程与极坐标
22.(10分)在直角坐标系xOy中,以坐标原点O为极点,以x轴为极轴建立极坐标系.已知直线l:(t为参数),曲线C的极坐标方程是ρ2﹣6ρcosθ+1=0,l与C相交于两点A、B.
(1)求l的普通方程和C的直角坐标方程;
(2)已知M(0,﹣1),求|MA|•|MB|的值.
【解答】解:(1)直线l的方程为:(t为参数),
转化为:x﹣y﹣1=0.
曲线C的极坐标方程是ρ2﹣6ρcosθ+1=0,
转化为:x2+y2﹣6x+1=0.
(2)把直线l的方程:(t为参数),代入x2+y2﹣6x+1=0得到:
,A点的参数为t1,B点的参数的为t2,
则:|MA|•|MB|=t1•t2=2.
选修4-5不等式选讲
23.已知正数a,b,c满足:a+b+c=1,函数f(x)=|x﹣|+|x+|.
(1)求函数f(x)的最小值;
(2)求证:f(x)≥9.
【解答】解(1)f(x)=|x﹣|+|x+|=||+|x+|
∵正数a,b,c,且a+b+c=1,
则(a+b+c)()=3+()=9
当且仅当a=b=c=时取等号.
∴f(x)的最小值为9.
(2)证明:f(x)=|x﹣|+|x+|=||+|x+|
∵正数a,b,c,且a+b+c=1,
则(a+b+c)()=3+()
=9
当且仅当a=b=c=时取等号.
∴f(x)≥9.