2020届二轮复习同角三角函数的基本关系及诱导公式课件（26张）（全国通用） 26页

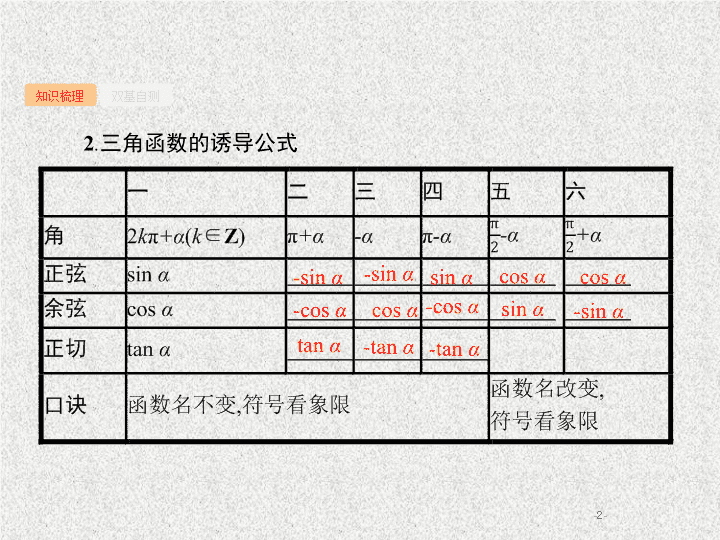
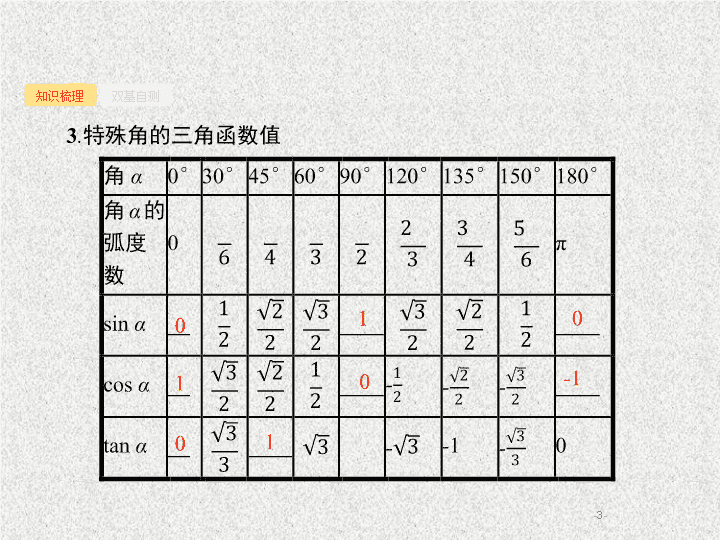
- 1 - 知识梳理 双基自测 1 . 同角三角函数的基本关系式 (1) 平方关系 :sin 2 α + cos 2 α = 　　　 .   1 tan α - 2 - 知识梳理 双基自测 2 . 三角函数的诱导 公式 - sin α 　 　 - sin α sin α cos α cos α - cos α cos α 　 - cos α sin α - sin α 　 tan α - tan α - tan α - 3 - 知识梳理 双基自测 3 . 特殊角的三角函数 值 0 　 　 1 0 　 　 1 0 　 　 - 1 0 　 　 1 2 - 4 - 知识梳理 双基自测 3 4 1 5 1 . 下列结论正确的打 “ √ ”, 错误的打 “×” . (1) 对任意的角 α , β , 都有 sin 2 α + cos 2 β = 1 . ( 　　 ) ( 3)sin( π + α ) =- sin α 成立的条件是 α 为锐角 . ( 　　 ) × × × × - 5 - 知识梳理 双基自测 2 3 4 1 5 答案 解析 解析 关闭 答案 解析 关闭 - 6 - 知识梳理 双基自测 2 3 4 1 5 答案 解析 解析 关闭 答案 解析 关闭 - 7 - 知识梳理 双基自测 2 3 4 1 5 答案 解析 解析 关闭 答案 解析 关闭 - 8 - 知识梳理 双基自测 2 3 4 1 5 5 . 已知 tan θ = 2, 则 sin θ cos θ = 　　　　　 .   答案 解析 解析 关闭 答案 解析 关闭 - 9 - 考点 1 考点 2 考点 3 思考 同角三角函数基本关系式有哪些用途 ? - 10 - 考点 1 考点 2 考点 3 - 11 - 考点 1 考点 2 考点 3 - 12 - 考点 1 考点 2 考点 3 A - 13 - 考点 1 考点 2 考点 3 例 2 已知关于 x 的方程 2 x 2 - ( + 1) x+m= 0 的两根为 sin θ 和 cos θ , 且 θ ∈ (0,2 π ) . ( 2) 求 m 的值 ; (3) 求方程的两根及此时 θ 的值 . 思考 sin α + cos α ,sin α - cos α ,sin α cos α 这三个式子之间有怎样的关系 ? - 14 - 考点 1 考点 2 考点 3 - 15 - 考点 1 考点 2 考点 3 - 16 - 考点 1 考点 2 考点 3 2 . 利用上述关系 , 对于 sin α + cos α ,sin α - cos α ,sin α cos α 这三个式子 , 可以知一求二 . - 17 - 考点 1 考点 2 考点 3 D C - 18 - 考点 1 考点 2 考点 3 - 19 - 考点 1 考点 2 考点 3 - 20 - 考点 1 考点 2 考点 3 - 21 - 考点 1 考点 2 考点 3 考向一 　 利用诱导公式化简三角函数 式 1 - 22 - 考点 1 考点 2 考点 3 解析 (1) 原式 =- sin 1 200 ° · cos 1 290 ° - cos 1 020 ° sin 1 050 ° =- sin(3 × 360 ° + 120 ° )cos(3 × 360 ° + 210 ° ) - cos(2 × 360 ° + 300 ° )sin(2 × 360 ° + 330 ° ) =- sin 120 ° cos 210 ° - cos 300 ° sin 330 ° =- sin(180 ° - 60 ° )cos(180 ° + 30 ° ) - cos(360 ° - 60 ° )sin(360 ° - 30 ° ) = sin 60 ° cos 30 ° + cos 60 ° sin 30 ° - 23 - 考点 1 考点 2 考点 3 思考 观察题目中的两角之间有什么关系 ? 当所给两角互补或互余时 , 怎样简化解题过程 ? - 24 - 考点 1 考点 2 考点 3 - 25 - 考点 1 考点 2 考点 3 解题心得 1 . 利用诱导公式化简三角函数的基本思路 :(1) 分析结构特点 , 选择恰当公式 ;(2) 利用公式化成单角三角函数 ;(3) 整理得最简形式 . 2 . 化简要求 :(1) 化简过程是恒等变形 ;(2) 结果要求项数尽可能少 , 次数尽可能低 , 结构尽可能简单 , 能求值的要求出值 . 3 . 用诱导公式求值时 , 要善于观察所给角之间的关系 , 利用整体 - 26 - 考点 1 考点 2 考点 3 A.{1, - 1,2, - 2} B.{ - 1,1} C.{2, - 2} D.{1, - 1,0,2, - 2} (2)sin 600 ° + tan 240 ° 的值等于 　　　　　 .   C