- 161.50 KB
- 2021-04-16 发布
12.2.2《三角形全等的判定》(SAS)导学案
【学习目标】
1、掌握三角形全等的“SAS”条件,能运用“SAS”证明简单的三角形全等问题
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3、积极投入,激情展示,做最佳自己。
学习重点:SAS的探究和运用.
学习难点:领会两边及其中一边的对角对应相等的两个三角形不一定全等.
【学习过程】
一、自主学习
1、复习思考
(1)怎样的两个三角形是全等三角形?全等三角形的性质是什么?三角形全等的判定(一)的内容是什么?
(2)上节课我们知道满足三个条件画两个三角形有4种情形,三个角对应相等;三条边对应相等;两角和一边对应相等;两边和一角对应相等;前两种情况已经研究了,今天我们来研究第三种两边和一角的情况,这种情况又要分两边和它们的夹角,两边及其一边的对角两种情况。
2、探究一:两边和它们的夹角对应相等的两个三角形是否全等?
(1)动手试一试
已知:△ABC
求作:,使,,
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(二):
两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(二)
在△ABC和中,
∵ ∴△ABC≌
3、探究二:两边及其一边的对角对应相等的两个三角形是否全等?
通过画图或实验可以得出:
4.例题学习
3
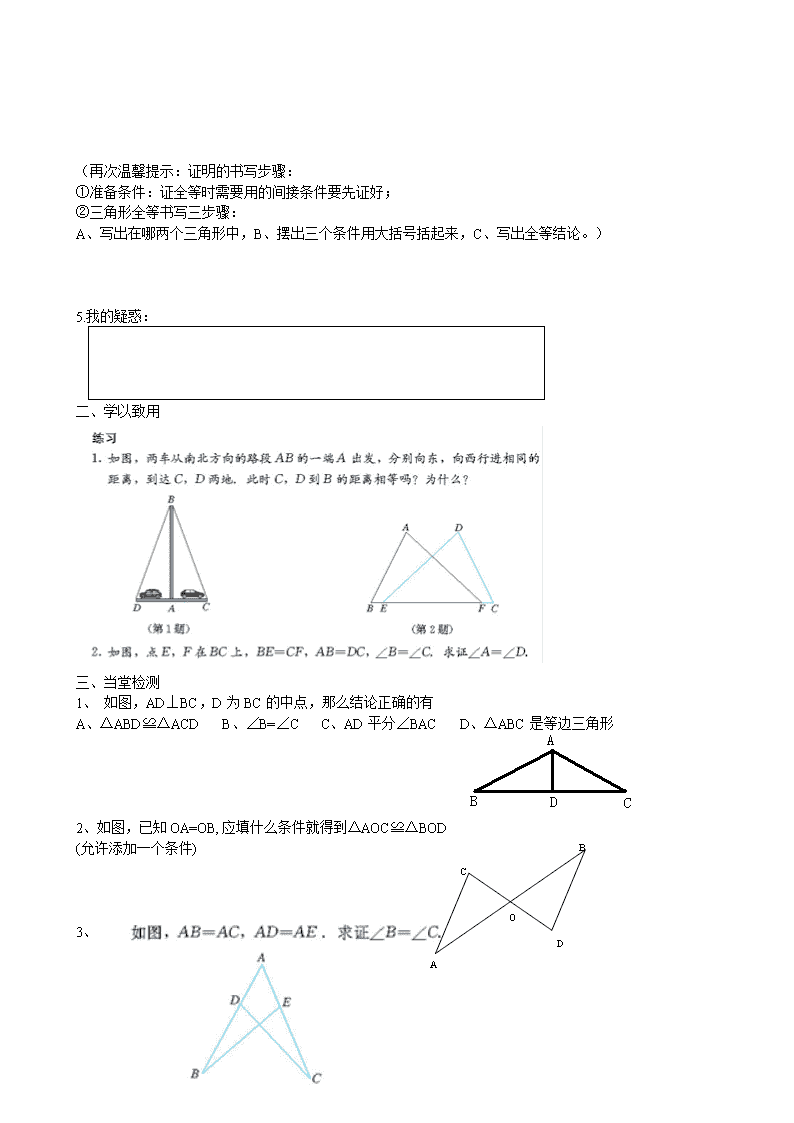
(再次温馨提示:证明的书写步骤:
①准备条件:证全等时需要用的间接条件要先证好;
②三角形全等书写三步骤:
A、写出在哪两个三角形中,B、摆出三个条件用大括号括起来,C、写出全等结论。)
5.我的疑惑:
二、学以致用
三、当堂检测
1、 如图,AD⊥BC,D为BC的中点,那么结论正确的有
A、△ABD≌△ACD B、∠B=∠C C、AD平分∠BAC D、△ABC是等边三角形
2、如图,已知OA=OB,应填什么条件就得到△AOC≌△BOD
(允许添加一个条件)
3、
3
﹡四、能力提升:(学有余力的同学完成)
如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN
五、课堂小结
1、两边和它们的夹角对应相等的两个三角形全等。简写成“ ”或“ ”
2、到目前为止,我们一共探索出判定三角形全等的2种方法,它们分别是: 和
3
相关文档
- 人教版九年级数学上册专题训练(七)2021-04-16 18:10:0221页
- 高中数学 1_1_1集合的含义与表示同2021-04-16 18:09:494页
- 新课标备战高考数学文专题复习60直2021-04-16 18:09:454页
- 2013年苏州中考数学试题 答案2021-04-16 18:09:4412页
- 【拔高卷】五年级上册数学重点小学2021-04-16 18:09:0713页
- 初中数学教师个人听课心得体会范文2021-04-16 18:08:2517页
- 北师大(2014秋)六年级上册数学试题-2021-04-16 18:08:1539页
- 人教新课标小学五年级数学第九册全2021-04-16 18:07:5968页
- 江西省遂川中学2017-2018学年高二2021-04-16 18:07:585页
- 中考数学总复习资料823332021-04-16 18:07:5879页