- 694.50 KB
- 2021-04-16 发布
2013年普通高等学校招生天津市南开区模拟考试(一)
数 学(文史类)
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分l50分,考试用时l20分钟.考试结束后,将本试卷和答题卡一并交回。
第I卷 (选择题共40分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.答在试卷上的无效.
3.本卷共8小题,每小题5分,共40分
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)计算(2+i)(-2+i)(i是虚数单位)的值等于
(A)5 (B)3 (C)-3 (D)-5
(2)的零点所在区间为
(A)(0,1) (B)(-1,0) (C)(1,2) (D)(-2,-l)
(3) 已知为等差数列{}的前n项和,S7=28,S11=66,则S9的值为
(A)47 (B)45 (C)38 (D)54
(4)设变量x,y满足制约条件则目标函数z=3x+5y的最大值为
(A)9 (B)-11 (C)17 (D)21
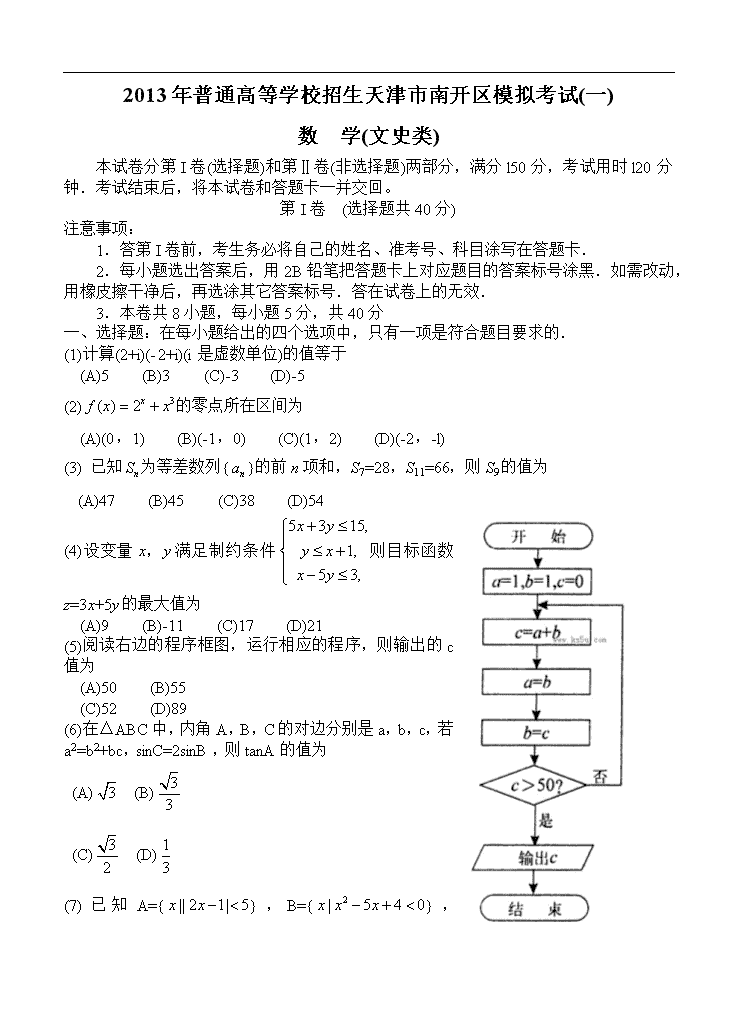
(5)阅读右边的程序框图,运行相应的程序,则输出的c值为
(A)50 (B)55
(C)52 (D)89
(6)在△ABC中,内角A,B,C的对边分别是a,b,c,若a2=b2+bc,sinC=2sinB,则tanA的值为
(A) (B)
(C) (D)
(7)已知A={},B={},
C=(1,3),则“”是“”的
(A)充分而不必要条件
(B)必要而不充分条件
(C)充要条件
(D)既不充分也不必要条件
(8) 已知直线l为抛物线(p>0)的准线,F为其焦点,直线AB经过F且与抛物线交于A,B两点。过点A,B做直线l的垂线,垂足分别为C,D,线段CD的中点为M,O为坐标原点,则下列命题中错误的是
(A)
(B)
(C)存在实数使得
(D)三角形AMB为等腰三角形
2013年普通高等学校招生天津市南开区模拟考试(一)
数 学(文史类)
第Ⅱ卷 (非选择题 共110分)
注意事项:
1.答卷前将密封线内的项目填写清楚.
2.用钢笔或圆珠笔直接答在试卷上.
3.本卷共12小题,共110分.
二、填空题:本大题共6小题.每小题5分.共30分.把答案填在题中横线上.
(9) (9)某校为了解高三男生的身体状况,检测了全部480名高三男生的体重(单位:kg),所得数据都在区间[50,75]中,其频率分布直方图如图所示.若图中从左到右的前3个小组的频率之比为1:2:3,则体重小于60kg的高三男生人数为 .
(10)一个几何体的三视图如右图所示(单位:cm),则这个几何体的体积为 立方厘米.
(11)已知圆C的方程为,直线l与x,y轴的交点坐标分别为(,0)和(0,),则直线l截圆C所得的弦长为
(12)已知正实数a,b满足a+b+2ab=1,则a+b的最小值为
(13)如图,A,B是两圆的交点,AC是小圆的直径,D和E分别是CA和CB的延长线与大圆的交点,已知AC=4,BE=10,且BC=AD,则DE=
(14)如图,在△ABC中,AD,BE分别为边BC,CA上的中线,且与的夹角为l20o,,则的值为 .
三、解答题:本大题6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
(15)(本小题满分l3分)
已知函数.
(I)求的值;
(Ⅱ)求f(x)的最大值及相应x的值.
(16)(本小题满分13分)
某公司由筛选出的男员工14名,女员工6名共20名员工组建甲、乙两个部门,现对这20名员工进行一次综合测试,成绩的茎叶图如下所示(单位:分)。现规定l80分以上者到“甲部门”工作,1 80分以下者到“乙部门”工作.
(I)求女员工成绩的平均值;
(II)现采用分层抽样的方式分“甲部门”和“乙部门”中共选取5人参加一项活动.
(i)甲、乙部门分别选取多少人?
(ii)若从这5人中随机的选出2人,那么至少一人选自“甲部门”的概率是多少?
(17)(本小题满分l3分).
如图,四边形ABCD是矩形,AD=2,DC=1,AB⊥平面BCE,BE⊥EC,EC=1.点F为线段BE的中点.
( I )求证:CE⊥平面ABE;
(Ⅱ)求证:DE∥平面A CF;
(Ⅲ)求AC和平面ABE所成角的正弦值。
(18)(本小题满分l3分)
已知数列{}满足,对一切有>0,,其中.
( I )求的值;
(II)求数列{}通项公式;
(Ⅲ)设数列{}满足,Tn为数列{}的前n项和,求Tn的表达式.
(19)(本小题满分l4分)
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线x2=4y的焦点,离心率等于.
( I )求椭圆C的方程;
(II)过椭圆C的右焦点F作直线l交椭圆C于A,B两点,交y轴于M点,若,求证为定值.
(20)(本小题满分l4分)
已知函数.
(I)当a=1时,求的极小值;
(II)若对于任意的[0,+∞),总有,求a的取值范围;
(III)设,求的最大值F(a)的解析式.