【数学】2018届一轮复习苏教版第74课时几何概型学案 4页

第74课时 几何概型 ‎【学习目标】‎ ‎1．了解几何概型的基本概念、特点和意义；了解测度的含义；‎ ‎2．理解几何概型的概率计算公式，并能运用其解决一些简单的几何概型的概率计算问题。‎ ‎【自主学习】‎ ‎1．在500ml的水中有一个草履虫，现从中随机取出2ml水样放到显微镜下观察，则发现草履虫的概率是 . ‎ ‎2. 取一根长度为‎3 m的绳子，拉直后在任意位置剪断，那么剪得两段的长都不小于‎1 m的概率是 . ‎ ‎3. 在‎1万 km2的海域中有40 km2的大陆架贮藏着石油，假如在海域中任意一点钻探，钻到油层面的概率是 . ‎ ‎4. 如下图，在一个边长为‎3 cm的正方形内部画一个边长为‎2 cm的正方形，向大正方形内随机投点，则所投的点落入小正方形内的概率是 .‎ ‎(第4题)‎ ‎ ‎ ‎5. 某人欲从某车站乘车出差，已知该站发往各站的客车均每小时一班，此人等车时间不多于10分钟的概率 ．‎ ‎6． 在圆心角为150°的扇形AOB中，过圆心O作射线交于P，则同时满足：∠AOP≥45°且∠BOP≥75°的概率为 ．‎ ‎7.在区间上任取两实数a,b，则二次方程x2+2ax+b2=0的两根都为实数的概率 .‎ ‎8.设有一个正方形网格，其中每个最小正方形的边长都为‎6cm，现用直径为‎2cm的硬币投掷到此网格上，则硬币落下后与格线有公共点的概率为 。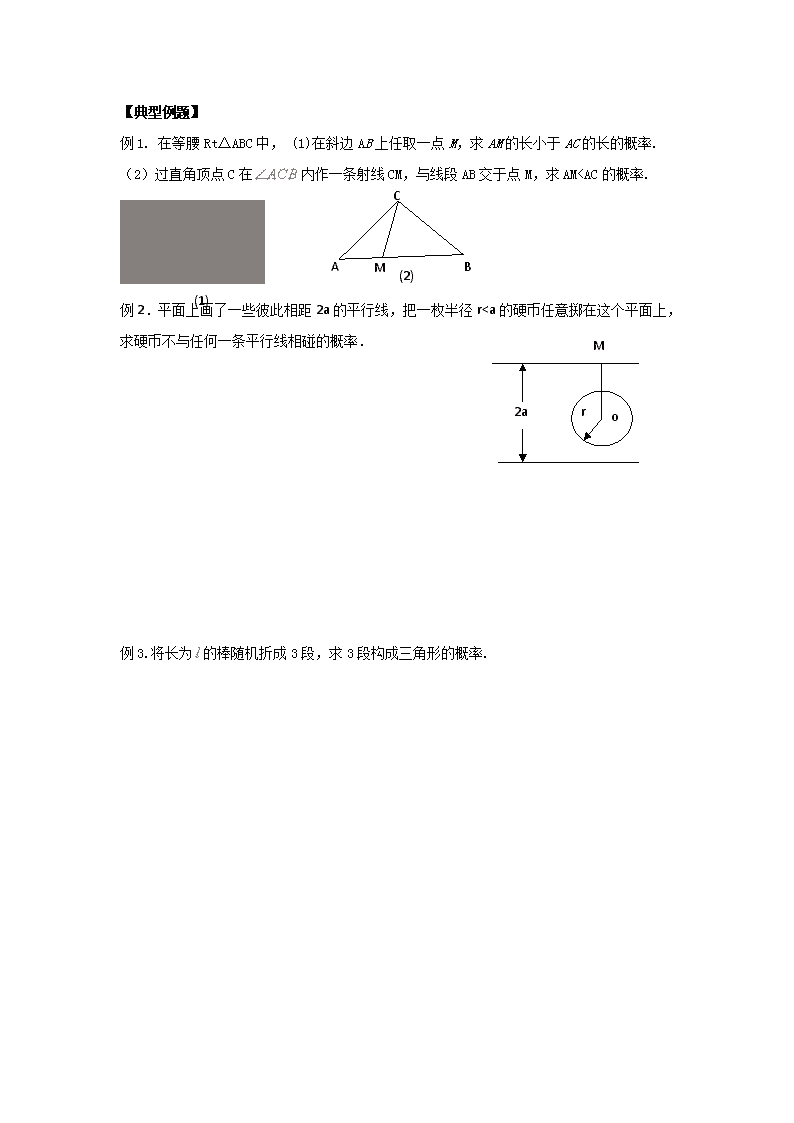‎ ‎【典型例题】‎ 例1. 在等腰Rt△ABC中， (1)在斜边AB上任取一点M，求AM的长小于AC的长的概率.‎ A C M ‎(2)‎ ‎（2）过直角顶点C在内作一条射线CM，与线段AB交于点M，求AM