- 630.50 KB
- 2021-04-16 发布
河北定州中学2016-2017学年第一学期
高二承智班数学周练试题(11)
一、选择题
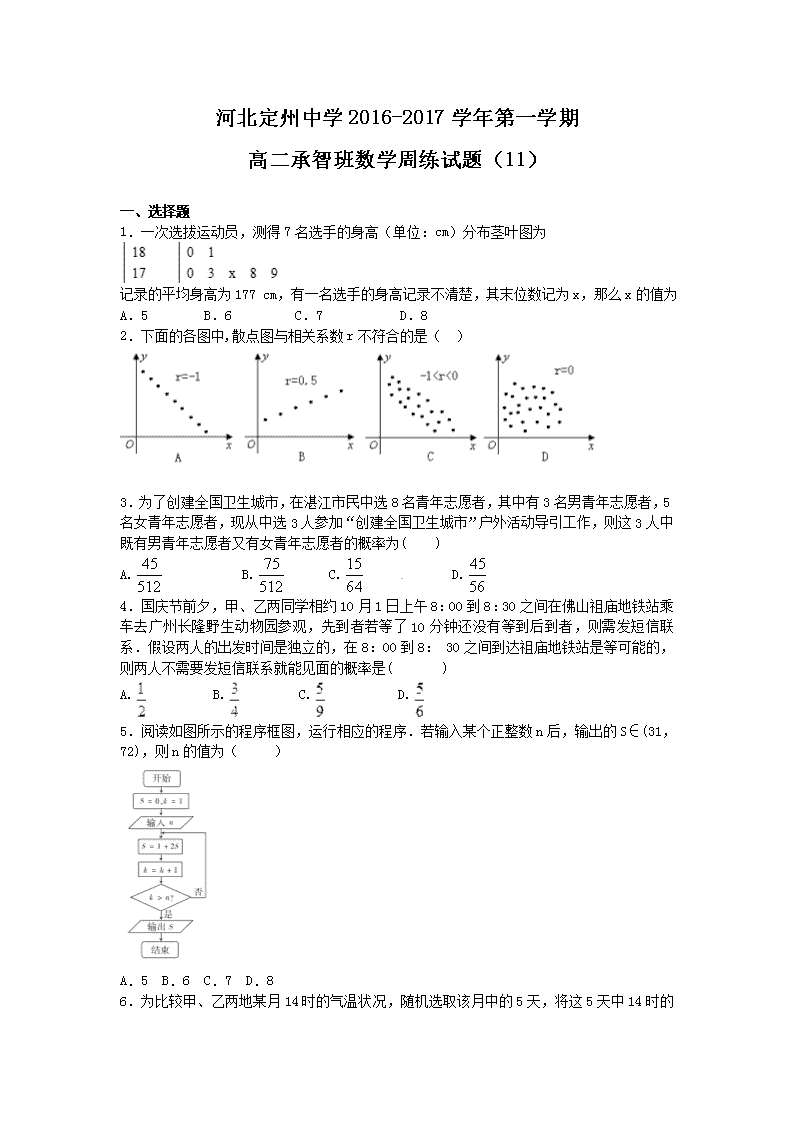
1.一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图为
记录的平均身高为177 cm,有一名选手的身高记录不清楚,其末位数记为x,那么x的值为
A.5 B.6 C.7 D.8
2.下面的各图中,散点图与相关系数r不符合的是( )
3.为了创建全国卫生城市,在湛江市民中选8名青年志愿者,其中有3名男青年志愿者,5名女青年志愿者,现从中选3人参加“创建全国卫生城市”户外活动导引工作,则这3人中既有男青年志愿者又有女青年志愿者的概率为( )
A. B. C. D.
4.国庆节前夕,甲、乙两同学相约10月1日上午8:00到8:30之间在佛山祖庙地铁站乘车去广州长隆野生动物园参观,先到者若等了10分钟还没有等到后到者,则需发短信联系.假设两人的出发时间是独立的,在8:00到8: 30之间到达祖庙地铁站是等可能的,则两人不需要发短信联系就能见面的概率是( )
A. B. C. D.
5.阅读如图所示的程序框图,运行相应的程序.若输入某个正整数n后,输出的S∈(31,72),则n的值为( )
A.5 B.6 C.7 D.8
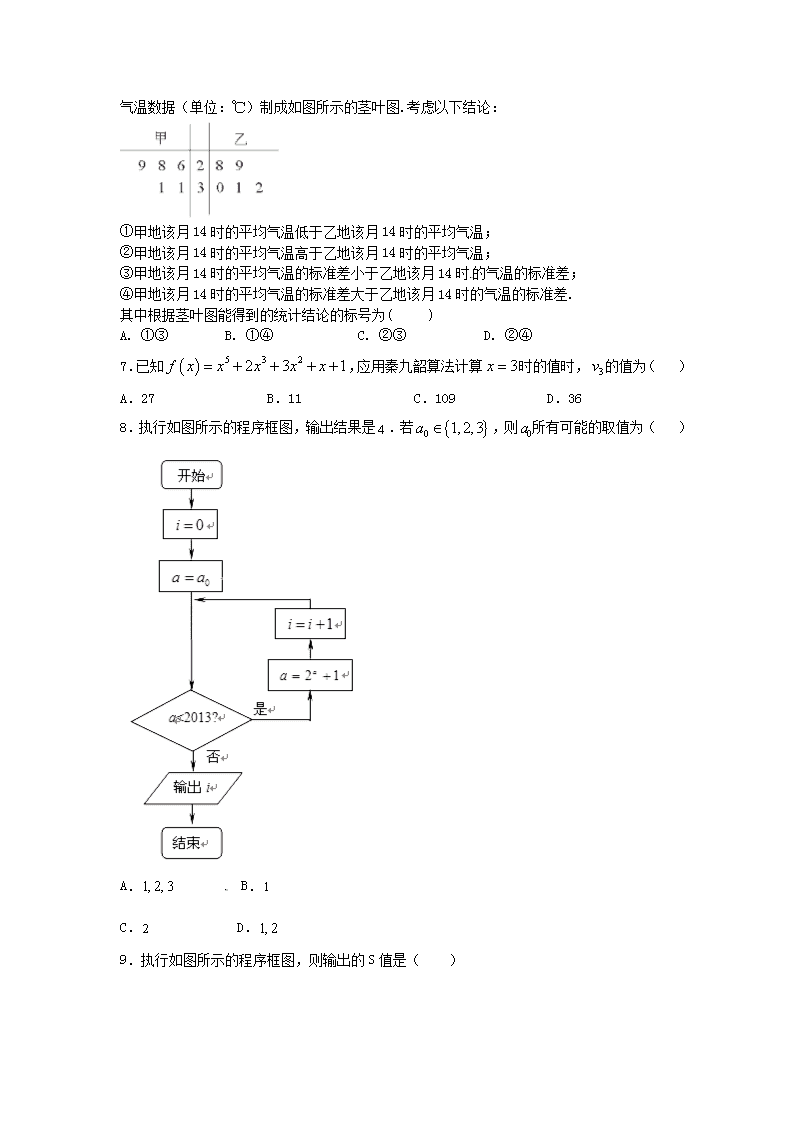
6.为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14
时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为( )
A. ①③ B. ①④ C. ②③ D. ②④
7.已知,应用秦九韶算法计算时的值时,的值为( )
A.27 B.11 C.109 D.36
8.执行如图所示的程序框图,输出结果是.若,则所有可能的取值为( )
A. B.
C. D.
9.执行如图所示的程序框图,则输出的S值是( )
A.﹣1 B. C. D.4
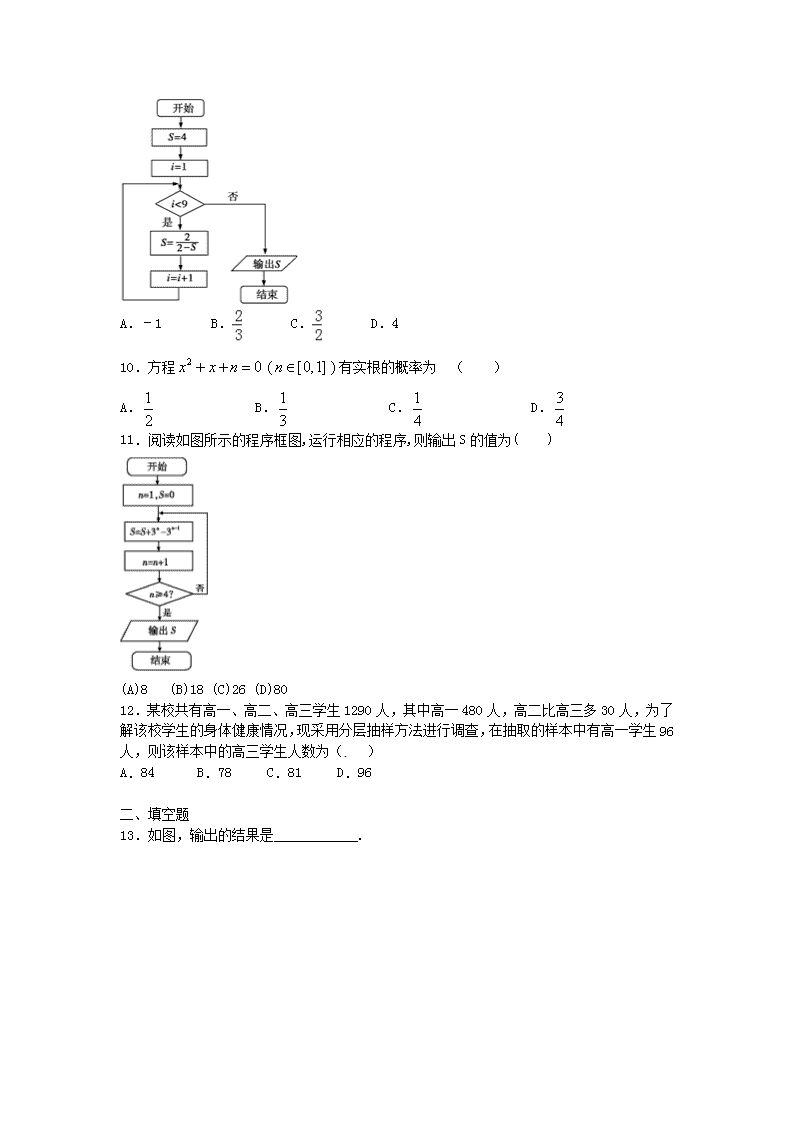
10.方程有实根的概率为 ( )
A. B. C. D.
11.阅读如图所示的程序框图,运行相应的程序,则输出S的值为( )
(A)8 (B)18 (C)26 (D)80
12.某校共有高一、高二、高三学生1290人,其中高一480人,高二比高三多30人,为了解该校学生的身体健康情况,现采用分层抽样方法进行调查,在抽取的样本中有高一学生96人,则该样本中的高三学生人数为( )
A.84 B.78 C.81 D.96
二、填空题
13.如图,输出的结果是 .
14.:一个总体分为A、B两层,用分层抽样方法从总体中抽取一个容量为30的样本,已知B层中每个个体被抽到的概率都是,则总体中的个体数为 。
15.已知正整数满足,则都是偶数的概率是 .
16.下图是一个算法流程图,若输入x的值为-4,则输出y的值为________.
三、解答题
17.设人的某一特征(如眼睛大小)是由他的一对基因所决定的,以x表示显性基因,y表示隐性基因,则具有xx基因的人为纯显性,具有yy基因的人是纯隐性。纯显性与混合性的人都有显露显性基因决定的某一特征,孩子从父母身上各得到1个基因。假定父母都是混合性,问:
(1)1个孩子由显性基因决定的特征的概率是多少?
(2)2个孩子中至少有一个显性基因决定的特征的概率是多少?
18.(本小题满分13分)为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
队别
北京
上海
天津
八一
人数
4
6
3
5
(Ⅰ)从这18名队员中随机选出两名,求两人来自同一支队的概率;
(Ⅱ
)中国女排奋力拼搏,战胜韩国队获得冠军.若要求选出两位队员代表发言,设其中来自北京队
的人数为,求随机变量的分布列,及数学期望.
19.(本小题满分12分)
某中学经市人民政府批准建分校,工程从2010年底开工到2013年底完工,工程分三期完成。经过初步招投标淘汰后,确定只由甲、乙两家建筑公司承建,且每期工程由两公司之一独立承建,必须在建完前一期工程后再建后一期工程。已知甲公司获得第一期、第二期、第三期工程承包权的概率分别为.
(1)求甲、乙两公司各至少获得一期工程的概率;
(2)求甲公司获得工程期数的分布列和数学期望.
20.(2009•全国卷Ⅱ)某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人.现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率.
参考答案
DBDCB BDBDC
11.C
12.B
13.12
14.:360;
15.
16.2
17.孩子的一对基因为xx,yy,xy的概率分别为,,,
且孩子有显性决定的特征是具有xx或xy,故
(1)1个孩子有显性决定的特征的概率为+=。
(2)因为2个孩子如果都不具有显性决定的特征,即2个孩子都具有yy基因的纯隐性特征,其概率为×=,所以2个孩子中至少有一个有显性决定特征的概率为1-=。
18.(Ⅰ);
(Ⅱ) 的分布列为:
0
1
2
P
.
(Ⅰ)“从这18名队员中随机选出两名,两人来自于同一队”记作事件A,
则.
(Ⅱ)的所有可能取值为0,1,2.
∵,,,
∴的分布列为:
0
1
2
P
∴.
19.
(1)记事件:“甲、乙两工程公司各至少获得一期工程”为事件A,
记事件:“甲、乙两工程公司各至少获得一期工程的对立事件”为. 则
= 5分
(2)由题意知,可能取的值为0,1,2,3
则
的分布列为
0
1
2
3
20.(1)见解析;
(2);
(3).
解:(1)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽取4名工人进行技术考核,则从每组各抽取2名工人.
(2)记A表示事件:从甲组抽取的工人中恰有1名女工人,则
(3)Ai表示事件:从甲组抽取的2名工人中恰有i名男工人,i=0,1,2
B表示事件:从乙组抽取的2名工人中恰有j名男工人,j=0,1,2
B表示事件:抽取的4名工人中恰有2名男工人.
Ai与Bj独立,i,j=0,1,2,且B=A0•B2+A1•B1+A2•B0
故P(B)=P(A0•B2+A1•B1+A2•B0)=P(A0)•P(B2)+P(A1)•P(B1)+P(A2)•P(B0)
==