- 975.00 KB
- 2021-04-16 发布
兴化市第一中学2018-2019年度十月份月考试卷
高三数学(文科)
命题人 沈旭东
一、填空题:()
1.已知集合,,则 ▲ .
2.命题“,”的否定是 ▲ .
3.若函数是偶函数,则实数 ▲ .
4.已知函数,,则 ▲ .
5.已知是的内角,则“”是“”的 ▲ 条件(填“充分不必要”、“必要不充分”、“充要条件”、“既不充分又不必要”之一)。
6.在中,,,,则 ▲ .
7.函数在区间上的最大值是 ▲ .
8.已知等差数列的前项和为,若,则 ▲ .
9.设曲线在点处的切线与直线平行,则的值是 ▲ .
10.设等比数列满足, ,则 ▲ .
11.已知数列满足,且,则 ▲
12.将函数的图象向左平移个单位长度,得到偶函数的图象,则的最大值是 ▲ .
13.在数列中,,,设,
是数列的前项和,则 ▲ .
14.如果函数在其定义域内总存在三个不同实数,,,满足,则称函数具有性质.已知函数具有性质 ,则实数的取值范围为 ▲ .、
二、解答题:
15.(本小题)设集合,.
(1)若且,求实数的值;
(2)若是的真子集,且,求实数的取值范围.
▲ ▲ ▲
16.(本小题)已知函数.
(Ⅰ)求的最小正周期;
(Ⅱ)求在上的单调递增区间.
▲ ▲ ▲
17.(本小题)已知函数
(1) 当时,试判断函数的奇偶性,并证明你的结论;
(2) 若不等式在上恒成立,求实数的取值范围.
▲ ▲ ▲
18.(本小题)已知函数.
(1)若,讨论的单调性;
(2)若在处取得极小值,求实数的取值范围 .
▲ ▲ ▲
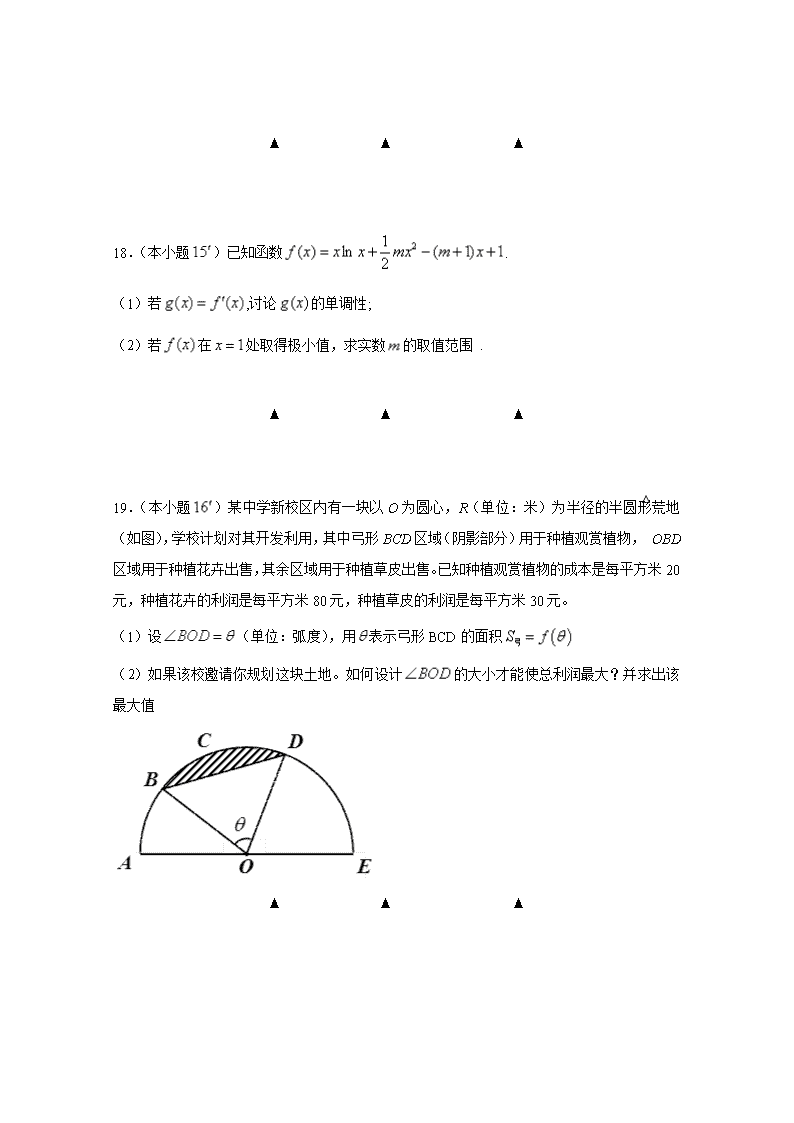
19.(本小题)某中学新校区内有一块以O为圆心,R(单位:米)为半径的半圆形荒地(如图),学校计划对其开发利用,其中弓形BCD区域(阴影部分)用于种植观赏植物,△OBD区域用于种植花卉出售,其余区域用于种植草皮出售。已知种植观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元。
(1)设(单位:弧度),用表示弓形BCD的面积
(2)如果该校邀请你规划这块土地。如何设计的大小才能使总利润最大?并求出该最大值
▲ ▲ ▲
20.(本小题)已知数列、是正项数列,为等差数列,为等比数列,的前项和为,且,,.
(1)求数列、的通项公式;
(2)令,求数列的前项和;
(3)设,若恒成立,求实数的取值范围.
▲ ▲ ▲
兴化市第一中学2018-2019年度十月份月考试卷
高三数学(文科)答案
一、填空题:()
1.已知集合,,则 ▲ .【答案】
2.命题“,”的否定是 ▲ .【答案】,
3.若函数是偶函数,则实数 ▲ .【答案】
4.已知函数,,则 ▲ .【答案】3
5.已知是的内角,则“”是“”的 ▲ 条件(填“充分不必要”、“必要不充分”、“充要条件”、“既不充分又不必要”之一)。【答案】充分不必要
6.在中,,,,则 ▲ .【答案】1
7.函数在区间上的最大值是 ▲ .【答案】
8.已知等差数列的前项和为,若,则 ▲ .【答案】36
9.设曲线在点处的切线与直线平行,则的值是 ▲ .【答案】1
10.设等比数列满足, ,则 ▲ .【答案】28
11.已知数列满足,且,则 ▲ 【答案】100
12.将函数的图象向左平移个单位长度,得到偶函数的图象,则的最大值是 ▲ .【答案】
13.在数列中,,,设,是数列的前项和,则 ▲ .【答案】
14.如果函数在其定义域内总存在三个不同实数,,,满足,则称函数具有性质.已知函数具有性质 ,则实数的取值范围为 ▲ .【答案】
【解析】由题意知:若 具有性质,则在定义域内有3个不同的实数根,
,
,即方程在R上有三个不同的实数根.
设 ,
当时,,即在上单调递增
当时,,所以在上单调递增,在上单调递减.
又 ,
方程在R上有三个不同的实数根即函数与的图象有三个交点.
, .故答案为:
二、解答题:
15.(本小题)设集合,.
(1)若且,求实数的值;
(2)若是的真子集,且,求实数的取值范围.
【答案】(1),
∵,∴ , ∴,
∵, ∴. 7分
(2)∵, ∴,
∵是的真子集, ∴ ,解得。
∴实数的取值范围解得. 14分
16.(本小题)已知函数.
(Ⅰ)求的最小正周期; (Ⅱ)求在上的单调递增区间.
【答案】(Ⅰ) .
所以的最小正周期为. 7分
(Ⅱ)由 , 得 .
当时,单调递增区间为和. 14分
17.(本小题)已知函数
(1) 当时,试判断函数的奇偶性,并证明你的结论;
(2) 若不等式在上恒成立,求实数的取值范围.
【答案】(1) 函数为偶函数
证明:函数的定义域为 时,,
所以函数为偶函数; 7分
(2) 由于得,即,
令, 原不等式等价于在上恒成立,
亦即在上恒成立
令, 当时,,
所以 15分
18.(本小题)已知函数.
(1)若,讨论的单调性;
(2)若在处取得极小值,求实数的取值范围 .
【答案】(1) .
①时,当时,,所以在上为增函数; 2分
②时,当时,,所以在上为增函数; 4分
③时,令 ,得,所以当时,;当时,,所以在上单调递增,在上单调递减; 6分
综上,时,在上为增;时,在上单增,在上单减. 7分
(2).当时,单增,恒满足,且函数在处极小10分
当时, 在单调递增,且,故即时,函数在处取得极小值. 综上所述,取值范围为. 14分
19.(本小题)某中学新校区内有一块以O为圆心,R(单位:米)为半径的半圆形荒地(如图),学校计划对其开发利用,其中弓形BCD区域(阴影部分)用于种植观赏植物,△OBD
区域用于种植花卉出售,其余区域用于种植草皮出售。已知种植观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元。
(1)设(单位:弧度),用表示弓形BCD的面积
(2)如果该校邀请你规划这块土地。如何设计的大小才能使总利润最大?并求出该最大值
【答案】
(1)扇形的面积
5分
(2)设总利润为元,种植草皮利润为元,种植花卉利润为元,种植学校观赏植物成本为元。
则
7分
设则,令,得,当时, , 单调递减;当时, , 单调递增。 10分
所以当时, 取得极小值,也是最小值为 12分
此时总利润最大,则最大总利润为 15分
所以当扇形的圆心角为时,总利润取得最大值为元 16分
20.(本小题)已知数列、是正项数列,为等差数列,为等比数列,的前项和为,且,,.(1)求数列、的通项公式;(2)令,求数列的前项和;(3)设,若恒成立,求实数的取值范围.
【答案】(1)设公差为,公比为,由已知得,,,
解之得:,.又因,故. 5分
(2), 所以, 7分
. 10分
(3),
当时,, 当时,, 13分
又因为,,,,所以的取值范围为. 16分