- 1.15 MB
- 2021-04-16 发布
南宁三中2017~2018学年度下学期高二月考(一)
文科数学试题
2018.3
一、选择题(本大题共12小题,每小题5分,共60分;每小题仅有一个答案是正确的,请选出正确答案。)
1.已知集合,那么( )
A. B.
C. D.
2.已知是虚数单位,则复数( )
A. B. C. D.
3.某城市收集并整理了该市2017年1月份至10月份各月最低气温与最高气温(单位:)的数据,绘制了下面的折线图。已知该市的各月
最低气温与最高气温具有较好的线性关系,
则根据该折线图,下列结论错误的是( )
A. 最低气温与最高气温为正相关
B. 10月的最高气温不低于5月的最高气温
C. 月温差(最高气温减最低气温)的
最大值出现在1月
D. 最低气温低于的月份有4个
4.已知曲线在点处切线的倾斜角为,则等于( )
A. 2 B. C. 3 D.
5.在中,分别为角的对边长,,则三角形的形状为( )
A. 等腰直角三角形 B. 等腰三角形或直角三角形
C. 正三角形 D. 直角三角形
6.设实数满足不等式组,则的取值范围是( )[]
A. B. C. D.
7.设,则“”是“”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
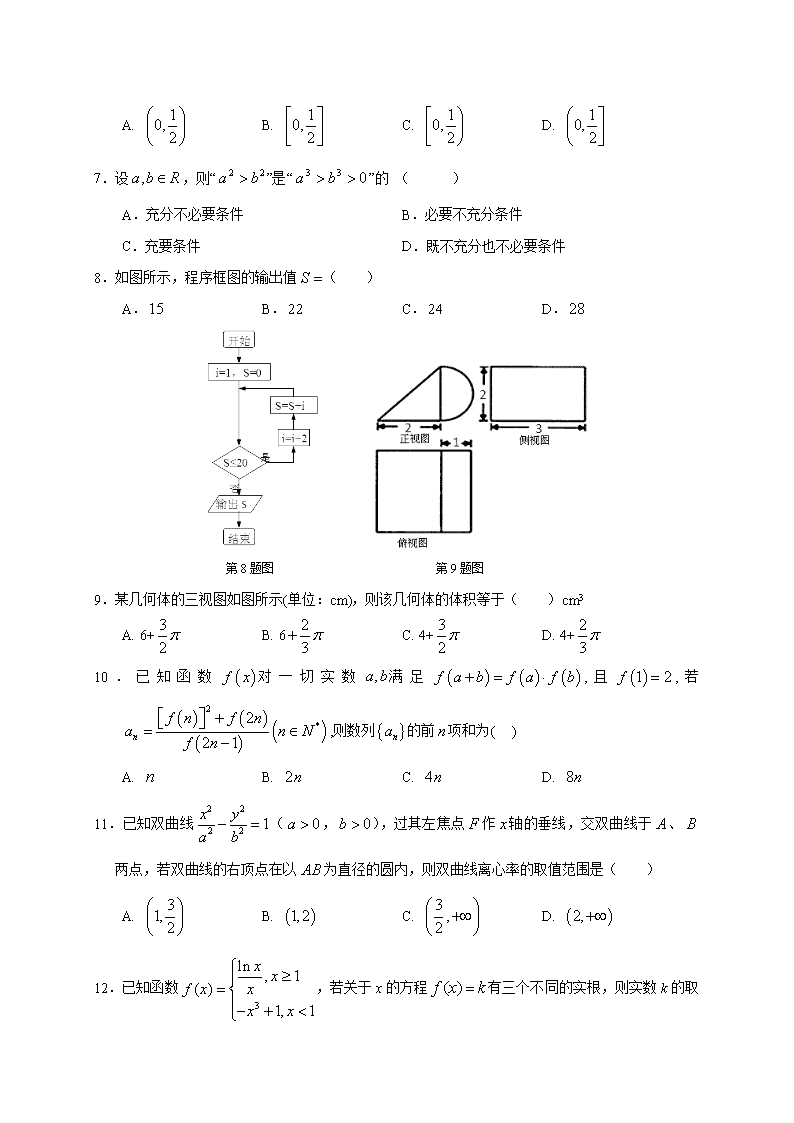
8.如图所示,程序框图的输出值( )
A. B. C. D.
第8题图 第9题图
9.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于( )cm3
A. 6+ B. 6 C. 4+ D. 4+
10.已知函数对一切实数满足,且,若,则数列的前项和为( )
A. B. C. D.
11.已知双曲线(,),过其左焦点作轴的垂线,交双曲线于、 两点,若双曲线的右顶点在以为直径的圆内,则双曲线离心率的取值范围是( )
A. B. C. D.
12.已知函数,若关于x的方程有三个不同的实根,则实数k
的取值范围是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.已知等差数列的9,则前13项的和为_____________.
14.若为锐角,,则__________.
15.设数列的前n项和为Sn,已知Sn=2n-an(n∈N+),通过计算数列的前四项,猜想___.
16.已知函数是定义在上的奇函数,,,则不等式的解集是__________.
三、解答题(本大题共6小题,第17小题10分,其余小题各12分,共70分)
17.(本题10分)在中,角所对边分别是,满足
(1)求角;
(2)若,求面积的最大值.
[来源:]
18.(本题12分)已知等差数列中,是数列的前项和,且
(1)求数列的通项公式;
(2)设数列的前项和为,求.
19.(本题12分)某小学为迎接校运动会的到来,在三年级招募了16名男志愿者和14名女志愿者.调查发现,男、女志愿者中分别各有10人和6人喜欢运动,其余人员不喜欢运动.
(1)根据以上数据完成2×2列联表,并说明是否有95%的把握认为性别与喜欢运动有关;
喜欢运动
不喜欢运动
总计
男
女
总计
(2)如果喜欢运动的女志愿者中恰有4人懂得医疗救护,现从喜欢运动的女志愿者中抽取2名负责处理应急事件,求抽出的2名志愿者都懂得医疗救护的概率.
附:K2=,
P(K2≥k0)
0.050
0.025
0.010
0.001
k0
3.841
5.024
6.635
10.828
20.(本题12分)如图,在三棱锥中,平面平面,,,,为线段上的点,且,.
(1)求证:平面;
(2)若,求点到平面的距离.
21.(本题12分)在平面直角坐标系中,动点P到两点的距离之和等于4,设动点P的轨迹为曲线C,直线过点且与曲线C交于A,B两点.
(1)求曲线C的方程;
(2)的面积是否存在最大值?若存在,求此时的面积,若不存在说明理由.
22.(本题12分)已知函数.
(1)求函数的单调区间;
(2)证明:.
南宁三中2017~2018学年度下学期高二月考(一)文科数学试题答案
1.A【解析】∵,故选:A。
2.C【解析】,选C.
3.D【解析】由图可以看出,当最低气温较大时,最高气温也较大,故A正确;10月份的最高气温大于20,而5月份的最高气温为不超过20,故B正确;从各月的温差看,1月份的温差最大,故C正确;而最低气温低于的月份是1,2,4三月份,故D错,选D.
4.A【解析】因为,所以,由已知得,解得,故选A.
5.D【解析】∵,∴,即,去分母得:
,即,则为直角三角形,故选D.
6.B【解析】作出不等式的可行域,如图所示:
可以看作阴影部分内的点(x,y)与定点P(-4,0)连线的斜率,
由图可知,AP的斜率最大,,
x轴上的点与P连线斜率最小为0,所以. 故选B.
7.B【解析】若,则,有;若,当时,
,所以“”是“”的必要不充分条件.
8.C【解析】由程序框图,得:;;;
;;结束循环,输出S值;故选C.
9.A【解析】根据三视图可知几何体是组合体:左边是直三棱柱、右边是半个圆柱,且三棱柱的底面是等腰直角三角形:直角边是2,高是3,圆柱的底面圆半径是1,母线长是3,∴几何体的体积,本题选择A选项.
10.C【解析】由,得
,…,,所以
,所以数列的前项和为.选C.
11.D【解析】是双曲线通径, ,由题意,即,,即,解得(舍去),故选D.
12.B【解析】由题意得当时,,所以当时,;当 时,,所以在上单调递增,在上单调递减,所以当时,取得极大值,又,当时,
,当时,函数为
减函数,作出的图象如图所示,所以当时,
有3个不同的实数根,故选B.
13.39【解析】由等差数列的性质知,,所以.
14.【解析】因为为锐角,,所以,
,故填.
15.【解析】当时,,解得,当时,,解得,当时,,解得,当时,,解得.故可猜想.
16.【解析】,设函数
的单调递增区间为
,单调递减区间为,所以当时,,当时,;当时,;当时,,因为不等式的解集等价于,所以当或时,,不等式的解集或,故答案为或.
17.【解析】(1)由已知得:,
则
∴,则
∵,∴,∵,∴
(2)由余弦定理得:
∴,当时取等号,∴
∴面积的最大值为
18.【解析】(1)设等差数列的首项为,公差为,因为
所以,得,
数列的通项公式是.
(2),=,
=,
==.
19.【解析】(1)
喜欢运动
不喜欢运动
总计
男
10
6
16
女
6
8
14
总计
16
14
30
由已知数据可得,
k=≈1.1575<3.841,因此,没有95%的把握认为性别与喜欢运动有关.
(2)喜欢运动的女志愿者有6人,分别设为A,B,C,D,E,F,其中A,B,C,D懂得医疗救护,则从这6人中任取2人的情况有(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种,
其中两人都懂得医疗救护的情况有(A,B),(A,C),(A,D),(B,C),(B,D),(C,D),共6种.
设“抽出的2名志愿者都懂得医疗救护”为事件A,则P(A)==.
20.【解析】(1)证明:连接,据题知
,则.
又因为,所以
因为,都在平面内,所以平面;
(2)
21.【解析】 (1)由椭圆的定义可知,点P的轨迹是椭圆
设椭圆方程为,由题意可得,,则
所以椭圆的方程为
(2)设直线,则,,
,,
∴,
令
∵
∴∴,则
22.【解析】(1)由题意可得,令,得.
当时,,函数单调递增;
当时,,函数单调递减.
所以的单调递增区间为,的单调递减区间为.
(2)要证成立,只需证成立.
令,则,令,则,
当时,,当时,,
所以在上单调递减,在上单调递增,所以,
又由(1)可得在上,
所以,所以不等式得证.