- 405.50 KB
- 2021-04-16 发布
2016-2017学年北京市昌平区临川学校高二(下)3月月考数学试卷(理科)
一、选择题(每题5分,共12小题,共60分,每题四个选项中只有一个选项是正确的,把选项填入答题卡的表格里)
1.下列导数公式错误的是( )
A.(sinx)'=﹣cosx B. C. D.(ex)'=ex
2.下列函数中,在(0,+∞)上为增函数的是( )
A.y=sin2x B.y=xex C.y=x3﹣x D.y=ln(1+x)﹣x
3.如图,函数y=f(x)的图象在点P处的切线方程是y=﹣x+8,则f(5)+f′(5)=( )
A. B.1 C.2 D.0
4.设函数f(x)=ax3+bx2+cx+2的导函数为f′(x),如果f′(x)为偶函数,则一定有( )
A.a≠0,c=0 B.a=0,c≠0 C.b=0 D.b=0,c=0
5.函数的图象在点(2,f(2))处的切线方程是( )
A.x﹣4y=0 B.x﹣4y﹣2=0 C.x﹣2y﹣1=0 D.x+4y﹣4=0
6.的值为( )
A.e+1 B.e﹣1 C.1﹣e D.e
7.f(x)与g(x)是定义在R上的两个可导函数,若f(x),g(x)满足f′(x)=g′(x),则f(x)与g(x)满足( )
A.f(x)=g(x) B.f(x)=g(x)=0
C.f(x)﹣g(x)为常数函数 D.f(x)+g(x)为常数函数
8.曲线y=x3﹣4x在点(1,﹣3)处的切线倾斜角为( )
A. B. C. D.
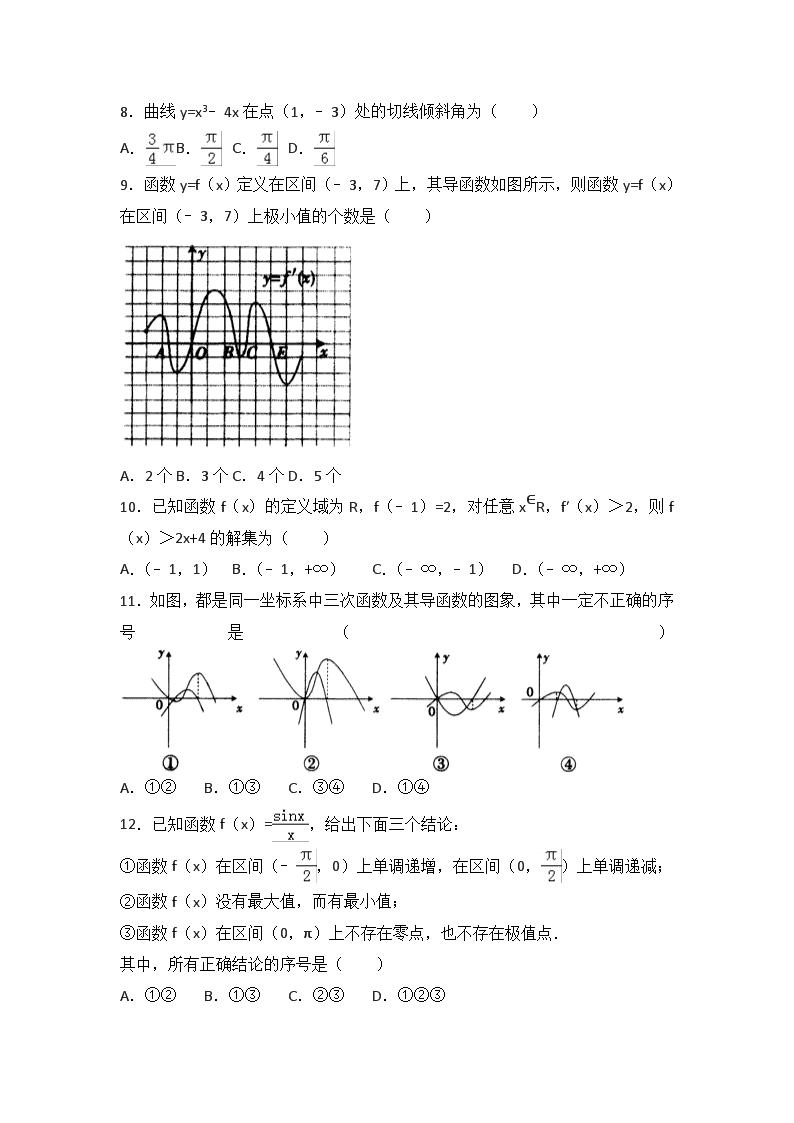
9.函数y=f(x)定义在区间(﹣3,7)上,其导函数如图所示,则函数y=f(x)在区间(﹣3,7)上极小值的个数是( )
A.2个 B.3个 C.4个 D.5个
10.已知函数f(x)的定义域为R,f(﹣1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
A.(﹣1,1) B.(﹣1,+∞) C.(﹣∞,﹣1) D.(﹣∞,+∞)
11.如图,都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是( )
A.①② B.①③ C.③④ D.①④
12.已知函数f(x)=,给出下面三个结论:
①函数f(x)在区间(﹣,0)上单调递增,在区间(0,)上单调递减;
②函数f(x)没有最大值,而有最小值;
③函数f(x)在区间(0,π)上不存在零点,也不存在极值点.
其中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(每题5分,共4小题,共20分,将答案填在答题卡的横线上)
13.已知函数f(x)=x2,则= .
14.曲线y=cosx(0≤x≤π)与坐标轴所围成的图形的面积为 ﹒
15.已知函数f(x)=2x3﹣3x,则在f(x)的切线中,斜率最小的一条切线方程为 .
16.已知定义在R上的函数f(x)满足f(2)=1,f′x)为f(x)的导函数.已知y=f′(x)的图象如图所示,若两个正数a,b满足f(2a+b)>1,则的取值范围是 .
三、解答题(本大题共6题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.已知曲线y=x2﹣1与y=1+x3在x=x0处的切线互相垂直,求x0的值.
18.设函数f(x)=﹣x3+2x2﹣x(x∈R).
(Ⅰ)求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)求函数在f(x)区间[0,2]上的最大值与最小值.
19.如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,设小正方形的边长为多少时,盒子容积最大?最大值为多少?
20.已知函数f(x)=ax3+bx2+4x的极小值为﹣8,其导函数y=f'(x)的图象经过点(﹣2,0),如图所示.
(Ⅰ)求f(x)的解析式;
(Ⅱ)求函数y=f(x)在区间[﹣3,2]上的最大值与最小值.
21.已知f(x)=x﹣lnx,g(x)=,其中x∈(0,e](e是自然常数).
(Ⅰ)求f(x)的单调性和极小值;
(Ⅱ)求证:g(x)在(0,e]上单调递增;
(Ⅲ)求证:f(x)>g(x)+.
22.设函数f(x)=xlnx(x>0).
(1)求函数f(x)的最小值;
(2)设F(x)=ax2+f′(x)(a∈R),讨论函数F(x)的单调性;
(3)斜率为k的直线与曲线y=f′(x)交于A(x1,y1)、B(x2,y2)(x1<x2)两点,求证:.
2016-2017学年北京市昌平区临川学校高二(下)3月月考数学试卷(理科)
参考答案与试题解析
一、选择题(每题5分,共12小题,共60分,每题四个选项中只有一个选项是正确的,把选项填入答题卡的表格里)
1.下列导数公式错误的是( )
A.(sinx)'=﹣cosx B. C. D.(ex)'=ex
【考点】导数的运算.
【分析】根据题意,依次计算选项函数的导数,比较即可得答案.
【解答】解:根据题意,依次分析选项:
对于A、(sinx)'=cosx,故A错误;
对于B、(lnx)′=,故B正确;
对于C、()′=x﹣1=(﹣1)×x﹣2=﹣,故C正确;
对于D、(ex)'=ex,故D正确;
故选:A.
2.下列函数中,在(0,+∞)上为增函数的是( )
A.y=sin2x B.y=xex C.y=x3﹣x D.y=ln(1+x)﹣x
【考点】利用导数研究函数的单调性.
【分析】欲判断函数的单调性,可考虑应用导数这个工具,令f′(x)>0求出递增区间,令f′(x)<0求出递减区间.从而对选项一一进行判断即可.
【解答】解:∵f(x)=sin2x=(1﹣cos2x)在(0,+∞)有增有减,∴A不正确;
∵f(x)=xex的导函数′(x)=ex(x+1)>0恒成立,所以它在(0,+∞)上增,∴
B正确;
∵y=x3﹣x,的导数y′=2x2﹣1在(0,+∞)上不恒大于0.,所以它在(0,+∞)先减后增,∴C不正确;
∵y=ln(1+x)﹣x的导数y′=﹣1在(0,+∞)恒小于0,所以它为减函数,∴D不正确.
故选B.
3.如图,函数y=f(x)的图象在点P处的切线方程是y=﹣x+8,则f(5)+f′(5)=( )
A. B.1 C.2 D.0
【考点】导数的运算.
【分析】利用函数在切点处的导数值是切线的斜率求出f′(5),将切点坐标代入切线方程求出f(5).
【解答】解:f′(5)=﹣1
将x=5代入切线方程得f(5)=﹣5+8=3,
所以f(5)+f′(5)=3+(﹣1)=2,
故选:C
4.设函数f(x)=ax3+bx2+cx+2的导函数为f′(x),如果f′(x)为偶函数,则一定有( )
A.a≠0,c=0 B.a=0,c≠0 C.b=0 D.b=0,c=0
【考点】导数的运算;函数奇偶性的判断.
【分析】先求导数f′(x),由f′(x)为偶函数可知f'(x)=f'(﹣x),故2bx=0恒成立,所以b=0,由此得出答案.
【解答】解:函数f(x)=ax3+bx2+cx+2的导函数为f′(x)=3ax2+2bx+c,
∵函数f′(x)=3ax2+2bx+c是定义在R上的偶函数,
∴f'(x)=f'(﹣x),即3ax2+2bx+c=3ax2﹣2bx+c,
∴2bx=0恒成立,b=0.
故选C.
5.函数的图象在点(2,f(2))处的切线方程是( )
A.x﹣4y=0 B.x﹣4y﹣2=0 C.x﹣2y﹣1=0 D.x+4y﹣4=0
【考点】利用导数研究曲线上某点切线方程.
【分析】求导函数,确定切线的斜率,求出切点的坐标,即可得到切线方程.
【解答】解:求导函数,可得
∴,f(2)=
∴函数的图象在点(2,f(2))处的切线方程是y﹣=(x﹣2),即x+4y﹣4=0
故选D.
6.的值为( )
A.e+1 B.e﹣1 C.1﹣e D.e
【考点】微积分基本定理.
【分析】直接利用积分基本定理即可求解
【解答】解:由积分基本定理可得, =
故选B
7.f(x)与g(x)是定义在R上的两个可导函数,若f(x),g(x)满足f′(x)=g′(x),则f(x)与g(x)满足( )
A.f(x)=g(x) B.f(x)=g(x)=0
C.f(x)﹣g(x)为常数函数 D.f(x)+g(x)为常数函数
【考点】导数的几何意义.
【分析】先根据导数的运算法则将f′(x)=g′(x)转化为[f(x)﹣g(x)]′=0,然后由函数的求导法则可得答案.
【解答】解:由f′(x)=g′(x),得f′(x)﹣g′(x)=0,
即[f(x)﹣g(x)]′=0,所以f(x)﹣g(x)=C(C为常数).
故选C.
8.曲线y=x3﹣4x在点(1,﹣3)处的切线倾斜角为( )
A. B. C. D.
【考点】导数的几何意义.
【分析】欲求在点(1,﹣3)处的切线倾斜角,先根据导数的几何意义可知k=y′|x=1,再结合正切函数的值求出角α的值即可.
【解答】解:.
故选A.
9.函数y=f(x)定义在区间(﹣3,7)上,其导函数如图所示,则函数y=f(x)在区间(﹣3,7)上极小值的个数是( )
A.2个 B.3个 C.4个 D.5个
【考点】函数的单调性与导数的关系.
【分析】函数在极小值点处,导数为0,且导函数左负右正,根据图象可得结论.
【解答】解:函数在极小值点处,导数为0,且导函数左负右正,
根据图象可知,O,C为极小值点,
故选:A.
10.已知函数f(x)的定义域为R,f(﹣1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
A.(﹣1,1) B.(﹣1,+∞) C.(﹣∞,﹣1) D.(﹣∞,+∞)
【考点】利用导数研究函数的单调性.
【分析】构造函数g(x)=f(x)﹣2x﹣4,利用导数研究函数的单调性即可得到结论.
【解答】解:设g(x)=f(x)﹣2x﹣4,
则g′(x)=f′(x)﹣2,
∵对任意x∈R,f′(x)>2,
∴对任意x∈R,g′(x)>0,
即函数g(x)单调递增,
∵f(﹣1)=2,
∴g(﹣1)=f(﹣1)+2﹣4=4﹣4=0,
则∵函数g(x)单调递增,
∴由g(x)>g(﹣1)=0得x>﹣1,
即f(x)>2x+4的解集为(﹣1,+∞),
故选:B
11.如图,都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是( )
A.①② B.①③ C.③④ D.①④
【考点】利用导数研究函数的单调性.
【分析】利用导数与函数之间的关系.把握住导数的正负确定出函数的单调区间,根据变化趋势选出不恰当的图象.利用排除法确定出答案.
【解答】解:根据f′(x)>0时,y=f(x)递增;f′(x)<0时,y=f(x)递减可得.
①②中函数的图象的增减趋势与导函数的正负区间是吻合的,可能正确;
而③中导函数为负的区间内相应的函数不为递减,故错误,
④中导函数为负的区间内相应的函数不为递减,故错误.
故选C.
12.已知函数f(x)=,给出下面三个结论:
①函数f(x)在区间(﹣,0)上单调递增,在区间(0,)上单调递减;
②函数f(x)没有最大值,而有最小值;
③函数f(x)在区间(0,π)上不存在零点,也不存在极值点.
其中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
【考点】命题的真假判断与应用.
【分析】由函数f(x)=表示(0,0)与(x,sinx)点连线的斜率,结合正弦型函数的图象和性质,逐一分析三个结论的真假,可得答案.
【解答】解:∵函数f(x)=表示(0,0)与(x,sinx)点连线的斜率,
∴当x∈(﹣,0)时,函数f(x)单调递增,
当x∈(0,)时,函数f(x)单调递减,故①正确;
当x→0时,f(x)→1,而x≠0,故f(x)<1,即函数没有最大值,
当(0,0)与(x,sinx)点连线与y=sin的图象相切时,f(x)有最小值,
故函数f(x)没有最大值,而有最小值,
故②正确;
当x∈(0,π)时,sinx≠0,故f(x)≠0,即函数f(x)在区间(0,π)上不存在零点,
而x∈(0,π)时,函数f(x)单调递减,也不存在极值,
故③正确;
故正确的结论的序号是①②③,
故选:D
二、填空题(每题5分,共4小题,共20分,将答案填在答题卡的横线上)
13.已知函数f(x)=x2,则= 0 .
【考点】变化的快慢与变化率.
【分析】先求出f′(x),由=f′(0),能求出结果.
【解答】解:∵f(x)=x2,
∴f′(x)=2x,
∴=f′(0)=0,
故答案为:0.
14.曲线y=cosx(0≤x≤π)与坐标轴所围成的图形的面积为 3 ﹒
【考点】余弦函数的图象.
【分析】根据面积等于cosx的绝对值在0≤x≤π上的积分可求出答案.
【解答】解:S==3
=3(sin﹣sin0)=3
故答案为3
15.已知函数f(x)=2x3﹣3x,则在f(x)的切线中,斜率最小的一条切线方程为 y=﹣3x .
【考点】利用导数研究曲线上某点切线方程.
【分析】先对f(x)=2x3﹣3x求导得y′=6x2﹣3,根据二次函数的单调性求出当x=0时其最小值为﹣3,据此求出切点,进而写出斜率最小时的切线方程.
【解答】解:∵f(x)=2x3﹣3x,∴f′(x)=6x2﹣3≥﹣3,
∴当x=0时,切线的斜率最小值且为﹣3,
当x=0时,f(0)=0,∴切点为(0,0),
∴切线的方程为y﹣0=﹣3(x﹣0),即y=﹣3x.
故答案为y=﹣3x.
16.已知定义在R上的函数f(x)满足f(2)=1,f′x)为f(x)的导函数.已知y=f′(x)的图象如图所示,若两个正数a,b满足f(2a+b)>1,则的取值范围是 (﹣,1) .
【考点】利用导数研究函数的单调性.
【分析】先根据导函数的图象判断原函数的单调性,从而确定a、b的范围,最后利用线性规划的方法得到答案.
【解答】解:由图可知,当x>0时,导函数f'(x)<0,原函数单调递减,
∵两正数a,b满足f(2a+b)>1,且f(2)=1,
∴2a+b<2,a>0,b>0,画出可行域如图.
k=的几何意义为点Q(2,1)与点P(x,y)连线的斜率,
当P点在A(1,0)时,k最大,最大值为:;
当P点在B(0,2)时,k最小,最小值为: =.
k的取值范围是(﹣,1).
故答案为:(﹣,1).
三、解答题(本大题共6题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.已知曲线y=x2﹣1与y=1+x3在x=x0处的切线互相垂直,求x0的值.
【考点】利用导数研究曲线上某点切线方程.
【分析】求导数,确定切线的向量,利用曲线y=x2﹣1与y=1+x3在x=x0处的切线互相垂直,建立方程,即可求x0的值.
【解答】解:由题意,
∵曲线y=x2﹣1与y=1+x3在x=x0处的切线互相垂直,
∴k1k2=﹣1,
∴.
18.设函数f(x)=﹣x3+2x2﹣x(x∈R).
(Ⅰ)求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)求函数在f(x)区间[0,2]上的最大值与最小值.
【考点】利用导数求闭区间上函数的最值;利用导数研究曲线上某点切线方程.
【分析】(I)根据导数的几何意义求出函数在x=2处的导数,从而得到切线的斜率,再利用点斜式方程写出切线方程即可.
(II)求导函数,确定函数的单调性,可得函数的极值与端点函数值比较,即可得到结论.
【解答】解:(Ⅰ)因为 f(x)=﹣x3+2x2﹣x,
所以 f'(x)=﹣3x2+4x﹣1,且f(2)=﹣2.…
所以 f'(2)=﹣5. …
所以 曲线f(x)在点(2,﹣2)处的切线方程是y+2=﹣5(x﹣2),
整理得5x+y﹣8=0. …
(Ⅱ)由(Ⅰ)知f'(x)=﹣3x2+4x﹣1=﹣(3x﹣1)(x﹣1).
令f'(x)=0,解得x=或x=1. …
当x∈[0,2]时,f'(x),f(x)变化情况如下表:
x
0
(0,)
(,1)
1
(1,2)
2
f'(x)
﹣
0
+
0
﹣
f(x)
0
↘
﹣
↗
0
↘
﹣2
因此,函数f(x),x∈[0,2]的最大值为0,最小值为﹣2.…
19.如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,设小正方形的边长为多少时,盒子容积最大?最大值为多少?
【考点】函数模型的选择与应用.
【分析】设小正方形的边长为xcm,则盒子容积为:y=(8﹣2x)•(5﹣2x)•x为三次函数,用求导法,可得x=1时,函数y取得最大值,此时盒子容积最大.
【解答】解:设小正方形的边长为xcm,则x∈(0,);
盒子容积为:y=(8﹣2x)•(5﹣2x)•x=4x3﹣26x2+40x,
对y求导,得y′=12x2﹣52x+40,令y′=0,得12x2﹣52x+40=0,解得:x=1,x=(舍去),
所以,当0<x<1时,y′>0,函数y单调递增;当1<x<时,y′<0,函数y单调递减;
所以,当x=1时,函数y取得最大值18;
所以,小正方形的边长为1cm,盒子容积最大,最大值为18cm3.
20.已知函数f(x)=ax3+bx2+4x的极小值为﹣8,其导函数y=f'(x)的图象经过点(﹣2,0),如图所示.
(Ⅰ)求f(x)的解析式;
(Ⅱ)求函数y=f(x)在区间[﹣3,2]上的最大值与最小值.
【考点】利用导数求闭区间上函数的最值;利用导数研究函数的极值.
【分析】(Ⅰ)根据题意可知函数在x=﹣2处取极小值8,由此列出方程组求出a和b,由此能求出f(x)的解析式.
(Ⅱ)由f′(x)=﹣3x2﹣4x+4=0,得,x2=﹣2,由此能求出函数y=f(x)在区间[﹣3,2]上的最大值,最小值.
【解答】解:(Ⅰ)根据题意可知函数在x=﹣2处取极小值8,
∵f(x)=ax3+bx2+4x,
∴f′(x)=3ax2+2bx+4
∴,
解得:a=﹣1,b=﹣2
∴f(x)=﹣x3﹣2x2+4x.
(Ⅱ)由(Ⅰ)得f′(x)=﹣3x2﹣4x+4,
由f′(x)=0,得,x2=﹣2,
∵f(﹣3)=﹣(﹣3)3﹣2(﹣3)2+4(﹣3)=﹣3,
f(﹣2)=﹣(﹣2)3﹣2(﹣2)2+4(﹣2)=﹣8,
f()=﹣()3﹣2()2+4×=﹣,
f(2)=﹣23﹣2•22+4•2=8.
∴函数y=f(x)在区间[﹣3,2]上的最大值为8,最小值为﹣8.
21.已知f(x)=x﹣lnx,g(x)=,其中x∈(0,e](e是自然常数).
(Ⅰ)求f(x)的单调性和极小值;
(Ⅱ)求证:g(x)在(0,e]上单调递增;
(Ⅲ)求证:f(x)>g(x)+.
【考点】利用导数求闭区间上函数的最值;利用导数研究函数的极值.
【分析】(Ⅰ)求导函数,利用导数的正负,可确定函数的单调性,从而可求f(x)的极小值;
(Ⅱ)求导数,利用0<x<e时,g'(x)>0,可得结论;
(Ⅲ)证明即可.
【解答】(Ⅰ)解:∵f(x)=x﹣lnx,∴f′(x)=(x>0),
∴当0<x<1时,f′(x)<0,此时f(x)单调递减;当1<x<e时,f′(x)>0,此时f(x)单调递增
∴f(x)的极小值为f(1)=1﹣﹣﹣﹣﹣﹣
(Ⅱ)证明:求导数可得
∴当0<x<e时,g'(x)>0,∴g(x)在(0,e]上单调递增﹣﹣﹣﹣﹣﹣
(Ⅲ)证明:∵f(x)的极小值为1,即f(x)在(0,e]上的最小值为1,∴f(x)>0,f(x)min=1
∴﹣﹣﹣﹣﹣﹣
∴f(x)>g(x)+.
22.设函数f(x)=xlnx(x>0).
(1)求函数f(x)的最小值;
(2)设F(x)=ax2+f′(x)(a∈R),讨论函数F(x)的单调性;
(3)斜率为k的直线与曲线y=f′(x)交于A(x1,y1)、B(x2,y2)(x1<x2)两点,求证:.
【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.
【分析】(1)根据极值与最值的求解方法,连续函数在区间(a,b)内只有一个极值,那么极小值就是最小值;
(2)先确定函数的定义域然后求导数Fˊ(x),讨论a在函数的定义域内解不等式Fˊ(x)>0和Fˊ(x)<0即可求得;
(3)要证,即证,等价于证,令,
则只要证,由t>1知lnt>0,故等价于证lnt<t﹣1<tlnt(t>1)即可.
【解答】(1)解:f′(x)=lnx+1(x>0),令f′(x)=0,得.
∵当时,f′(x)<0;当时,f′(x)>0,
∴当时,.
(2)F(x)=ax2+lnx+1(x>0),.
①当a≥0时,恒有F'(x)>0,F(x)在(0,+∞)上是增函数;
②当a<0时,
令F′(x)>0,得2ax2+1>0,解得;
令F′(x)<0,得2ax2+1<0,解得.
综上,当a≥0时,F(x)在(0,+∞)上是增函数;
当a<0时,F(x)在上单调递增,在上单调递减.
(3)证:.
要证,即证
,等价于证,令,
则只要证,由t>1知lnt>0,故等价于证lnt<t﹣1<tlnt(t>1)(*).
①设g(t)=t﹣1﹣lnt(t≥1),则,故g(t)在[1,+∞)上是增函数,
∴当t>1时,g(t)=t﹣1﹣lnt>g(1)=0,即t﹣1>lnt(t>1).
②设h(t)=tlnt﹣(t﹣1)(t≥1),则h′(t)=lnt≥0(t≥1),故h(t)在[1,+∞)上是增函数,
∴当t>1时,h(t)=tlnt﹣(t﹣1)>h(1)=0,即t﹣1<tlnt(t>1).
由①②知(*)成立,得证.