- 850.50 KB
- 2021-04-16 发布
黄冈市2018-2019学年高二下学期期末考试
数学理试题2019年7月1日
一、选择题(本大题共12个小题,每小题5分,共60分)
1、若复数z满足z(1+i)=4-2i(i为虚数单位),则=( )
A、1+3i B、1-3i C、-1-3i D、-1+3i
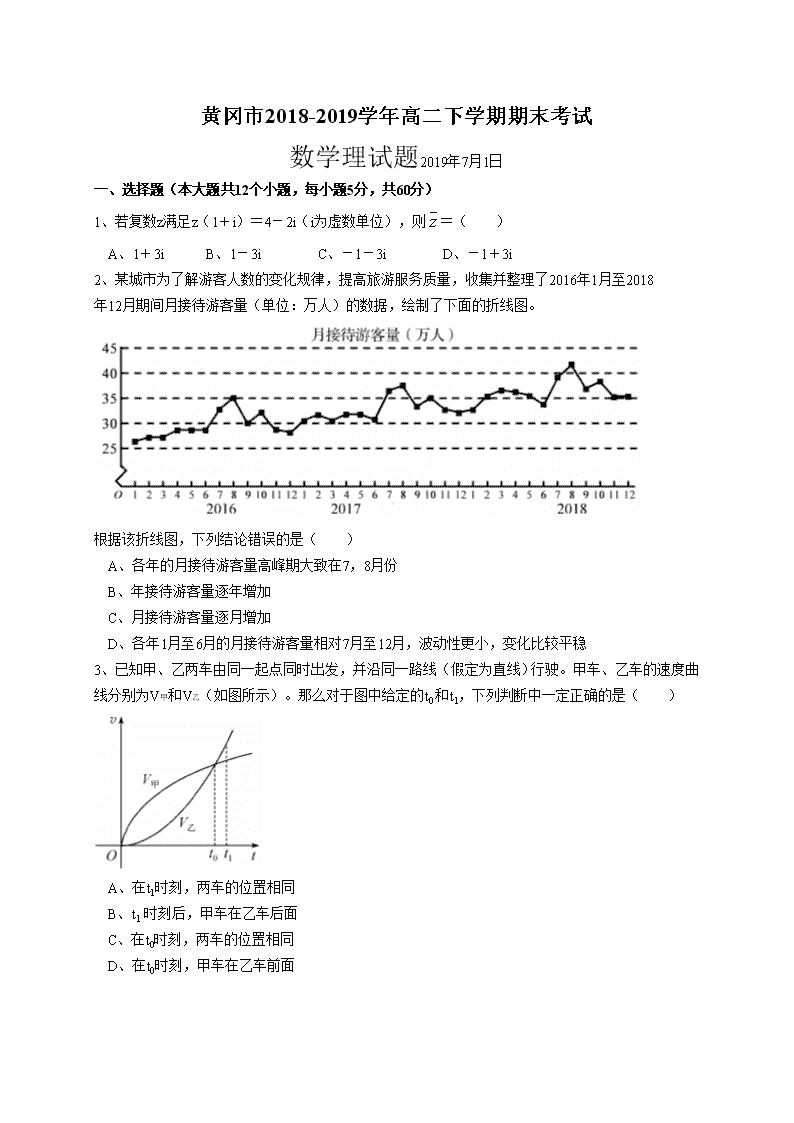
2、某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018
年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图。
根据该折线图,下列结论错误的是( )
A、各年的月接待游客量高峰期大致在7,8月份
B、年接待游客量逐年增加
C、月接待游客量逐月增加
D、各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳
3、已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶。甲车、乙车的速度曲线分别为V甲和V乙(如图所示)。那么对于图中给定的t0 和t1,下列判断中一定正确的是( )
A、在t1时刻,两车的位置相同
B、t1 时刻后,甲车在乙车后面
C、在t0时刻,两车的位置相同
D、在t0时刻,甲车在乙车前面
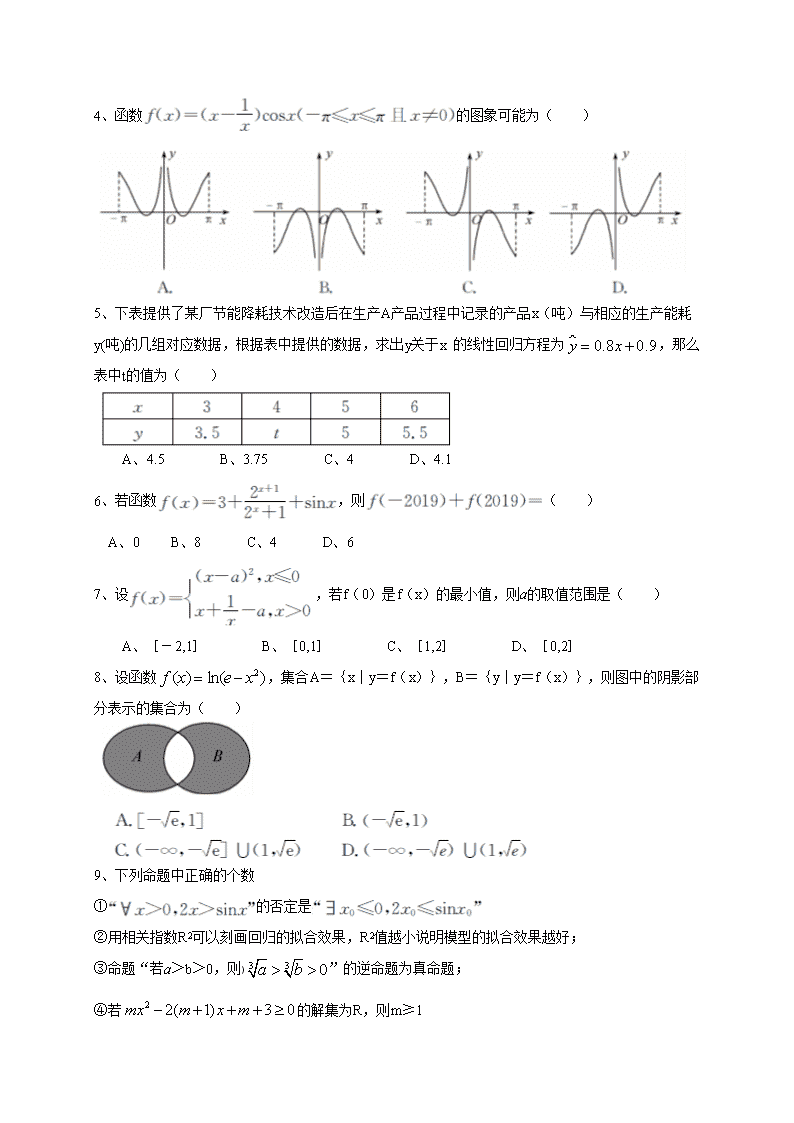
4、函数的图象可能为( )
5、下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产品x(吨)与相应的生产能耗y(吨)的几组对应数据,根据表中提供的数据,求出y关于x 的线性回归方程为,那么表中t的值为( )
A、4.5 B、3.75 C、4 D、4.1
6、若函数,则( )
A、0 B、8 C、4 D、6
7、设,若f(0)是f(x)的最小值,则a的取值范围是( )
A、[-2,1] B、[0,1] C、[1,2] D、[0,2]
8、设函数,集合A={x|y=f(x)},B={y|y=f(x)},则图中的阴影部分表示的集合为( )
9、下列命题中正确的个数
①的否定是
②用相关指数R2可以刻画回归的拟合效果,R2值越小说明模型的拟合效果越好;
③命题“若a>b>0,则)”的逆命题为真命题;
④若的解集为R,则m≥1
A、0 B、1 C、2 D、3
10、只用1,2,3,4四个数字组成一个五位数,规定这四个数字必须同时使用,且同一数字不能
相邻出现,这样的四位数有( )
A、96 B、144 C、240 D、288
111已知函数时,不等式恒成立,则实数a的取值范围为( )
12、某商场进行购物摸奖活动,规则是:在一个封闭的纸箱中装有标号分别为1,2,3,4,5,6的
六个小球,每次摸奖需要同时取出两个球,每位顾客最多有两次摸奖机会,并规定:若第一次取出的两球号码连号,则中奖,摸奖结束;若第一次未中奖,则将这两个小球放回后进行第二次摸球,若与第一次取出的两个小球号码相同,则为中奖。按照这样的规则摸奖,中奖的概率为( )
二、填空题(本大题共4小题,每小题5分,共20分)
13、若,则x+y=___
14、若1的展开式的第3项的二项式系数为36,则其展开式中的常数项为
______
15、在某校举行的数学竞赛中0全体参赛学生的竞赛成绩近似服从正态分布N(70,100)。已知成绩在80到90分之间的学生有120名,若该校计划奖励竞赛成绩在90分以上(含90分)的学生,估计获奖的学生有__人(填一个整数)
(参考数据:若有,
16、若函数有两个极值点x1,x2,其中,
且x1<f(x2)<x2,则方程的实根个数为___个
三、解答题(本大题共6个小题,满分70分。解答应写出文字说明0证明过程或演算步骤)
17、(本小题满分12分)
已知函数在R上是奇函数,且在x=1处取得极小值-2。
(1)求的解析式;
(2)求过点A(0,16)且与曲线相切的切线方程。
18、(本小题满分12分)
为了适应高考改革,某中学推行“创新课堂”教学。高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取20名学生的成绩进行统计分析,结果如下表:(记成绩不低于120分者为“成绩优秀”)
(I)由以上统计数据填写下面的2×2列联表,并判断是否有95%以上的把握认为“成绩优秀与教学方式有关”?
(II)现从上述样本“成绩不优秀”的学生中,抽取3人进行考核,记“成绩不优秀”的乙班人
数为X,求X的分布列和期望。
参考公式
临界值表
19、(本小题满分12分)
已知。
(I)讨论的单调性;
(II)若,且g(x)在区间[1,e]上的最小值为,
求a的值。
20、(本小题满分12分)
某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶5元,售价每瓶7元,未售出的酸奶降价处理,以每瓶3元的价格当天全部处理完,根据往年销售经验,每天需求量与当天最高气温(单位:°C)有关。如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶。为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n
(单位:瓶)为多少时,Y的数学期望达到最大值?
21、(本小题满分12分)
已知函数在其定义域内有两个不同的极值点.
(1)求m的取值范围。
(2)试比较20182019与20192018的大小,并说明理由;
(3)设的两个极值点为x1,x2,证明x1x2>e2。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分,解答时请写清
题号。
22、(选修4-4:极坐标系与参数方程)
在直角坐标系xoy中,直线l的参数方程为(t为参数),以坐标原点为极点,
x轴正半轴为极轴建立极坐标系,圆C极坐标方程为。
(1)求直线l的普通方程和圆C的直角坐标方程;
(2)若直线l与圆C相切,求m的值。
23.(选修4-5:不等式选讲)
已知函数
(1)解不等式;
(2)当[1,2]时,恒成立,求实数a的取值范围。
2019年春季高二期末数学试题答案(理科)
一、选择题
1. A 2.C 3. D 4. C 5.C 6.B 7.B 8.C 9.C 10.B 11. A 12. B
二、填空题
13. 2 14. 15. 20 16. 4个.
三、解答题
17.解析:(1)函数在是奇函数,所以
………………6分
(2)设切点为,则点M的坐标满足.
因,故切线的方程为,
注意到点在切线上,有,
化简得:,解得.
所以,切点为,切线方程为.………………12分
18.解:(1)补充的列联表如下表:
传统教学
创新教学
总计
成绩优秀
10
26
成绩不优秀
10
14
总计
根据列联表中的数据,得的观测值为,
所以有以上的把握认为“成绩优秀与教学方式有关”.………………5分
(2)的可能取值为,,,,
,………………6分
,………………7分
,………………8分
,………………9分
所以的分布列为
………10分
………………12分
19.解:(I)的定义域为,.若,则,所以在上单调递增.若,则当时,;当时,.所以在上单调递增,在上单调递减.…………4分
(2)由得.
当,即时,在上为增函数,∴,得,与矛盾.
当,即时,在上为减函数,在上为增函数,∴
,得,满足.
当,即时,在上为减函数,∴,得,与矛盾.
综上,得.………………12分
20.解:(1)由题意得,可取
的分布列为
………………4分
(2)由题意可知
①当时,若,
则
若时,则
若时,则,
的分布列为
∴,
∴当时,(元)
②当时,若,
则
若时,则
若时,则
Y的分布列为
Y
(元)
∴综上,当为瓶时,Y的数学期望达到最大值。………………12分
21.解析:(1)依题意,函数的定义域为,所以方程在有两个不同根.即方程在有两个不同根.
转化为,函数与函数的图象在上有两个不同交点
又,即时, , 时,,
所以在上单调增,在上单调减,从而.
又有且只有一个零点是1,且在时,,在时, ,所以由的图象,
要想函数与函数的图象在上有两个不同交点,
只需,即 ………………3分
(2)由(1)所以在上单调增,在上单调减,所以,即,
, ………………6分科网]
(3) 由(1)可知分别是方程的两个根,
即, ,
设,作差得, ,即.
原不等式等价于
令,则,, [来源:Z&xx&k.Com]
设, ,,
∴函数在上单调递增,
∴,
即不等式成立,故所证不等式成立.………………12分
22.(选修4-4:极坐标系与参数方程)
解:(1)由题意得,直线的普通方程为,
圆的直角坐标方程为. ………………5分
(2)因为直线与圆相切,所以,解得;
所以的值为. …………………………10分
23.(选修4-5:不等式选讲)
解:(1)原不等式等价于 或或
解得,所以不等式的解集为 …………………5分
(2)当时,,不等式可以化为,
因为,,所以,
所以。 ……………………10分