【精品】人教版 九年级下册数学 28 8页

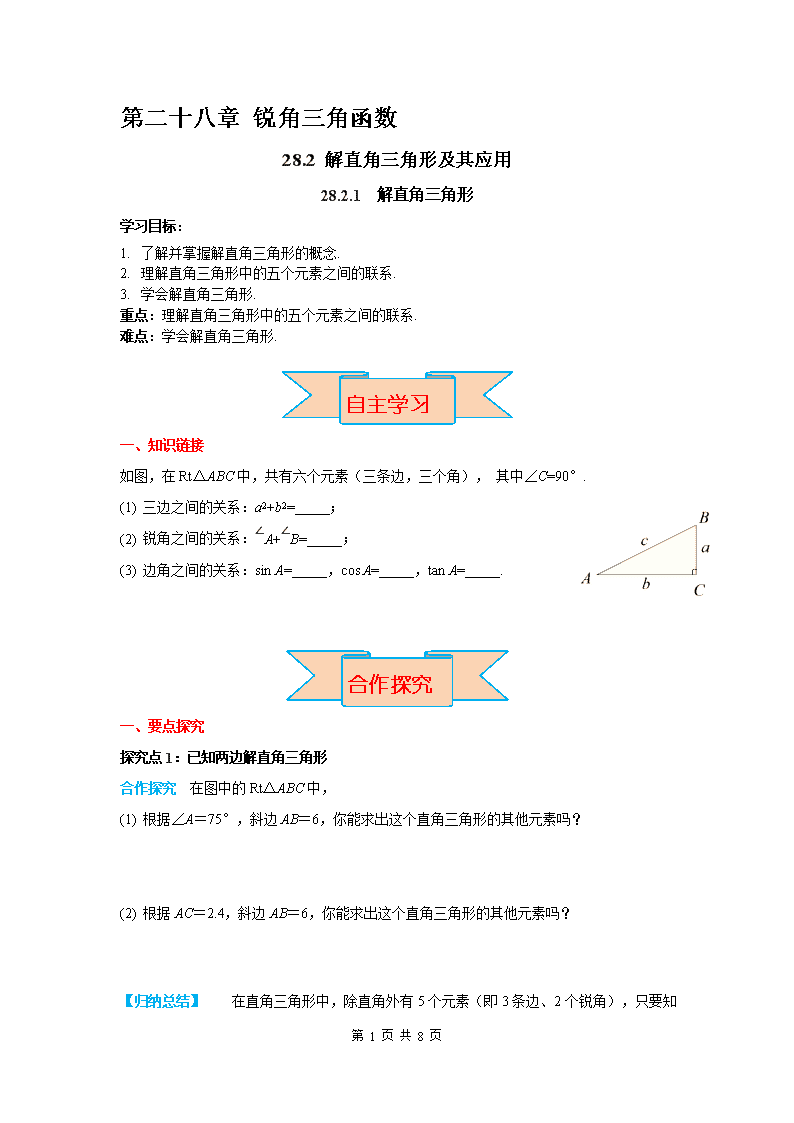
第 1 页 共 8 页 第二十八章 锐角三角函数 28.2 解直角三角形及其应用 28.2.1 解直角三角形 学习目标： 1. 了解并掌握解直角三角形的概念. 2. 理解直角三角形中的五个元素之间的联系. 3. 学会解直角三角形. 重点：理解直角三角形中的五个元素之间的联系. 难点：学会解直角三角形. 自主学习 一、知识链接 如图，在 Rt△ABC 中，共有六个元素（三条边，三个角）， 其中∠C=90°. (1) 三边之间的关系：a2+b2=_____； (2) 锐角之间的关系：∠A+∠B=_____； (3) 边角之间的关系：sin A=_____，cos A=_____，tan A=_____. 合作探究 一、要点探究 探究点 1：已知两边解直角三角形 合作探究 在图中的 Rt△ABC 中， (1) 根据∠A＝75°，斜边 AB＝6，你能求出这个直角三角形的其他元素吗？ (2) 根据 AC＝2.4，斜边 AB＝6，你能求出这个直角三角形的其他元素吗？ 【归纳总结】 在直角三角形中，除直角外有 5 个元素（即 3 条边、2 个锐角），只要知 第 2 页 共 8 页 道其中的 2 个元素（至少有 1 个是边），就可以求出其余的 3 个未知元素. 由直角三角形中的已知元素，求出其余未知元素的过程，叫做解直角三角形. 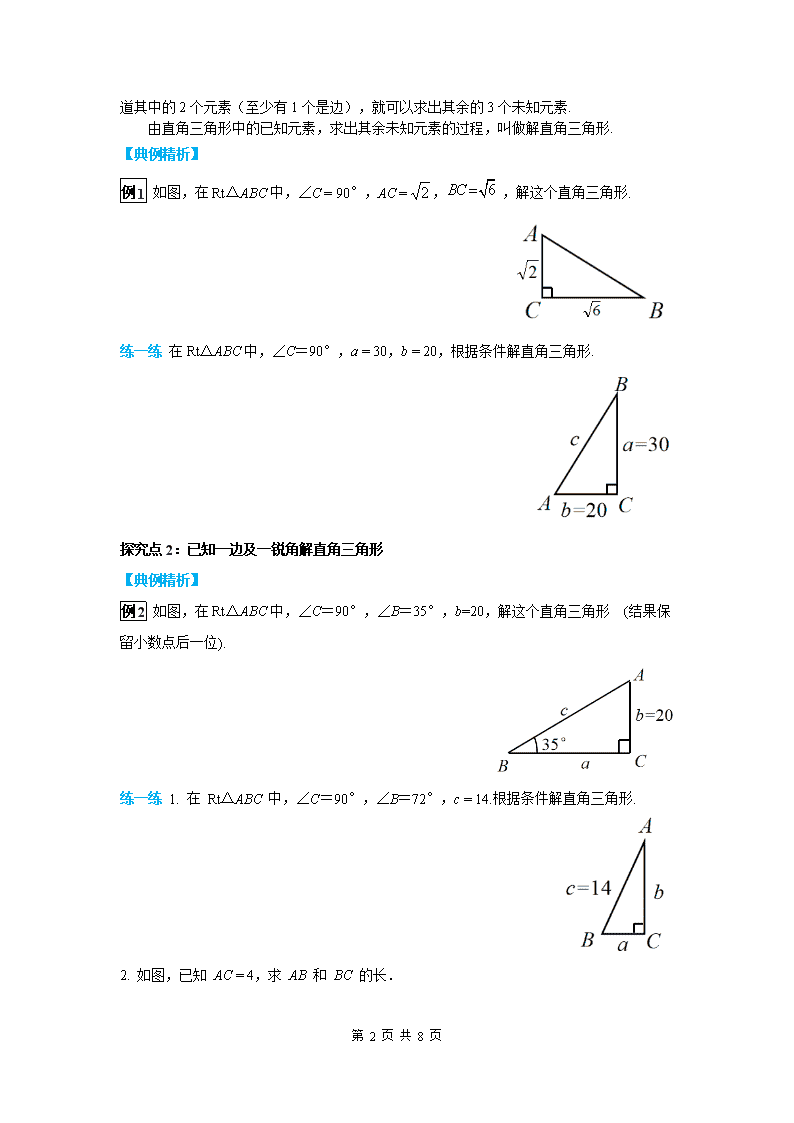【典例精析】 例 1 如图，在 Rt△ABC 中，∠C = 90°，AC = 2 ， 6BC ，解这个直角三角形. 练一练 在 Rt△ABC 中，∠C＝90°，a = 30，b = 20，根据条件解直角三角形. 探究点 2：已知一边及一锐角解直角三角形 【典例精析】 例 2 如图，在 Rt△ABC 中，∠C＝90°，∠B＝35°，b=20，解这个直角三角形 (结果保 留小数点后一位). 练一练 1. 在 Rt△ABC 中，∠C＝90°，∠B＝72°，c = 14.根据条件解直角三角形. 2. 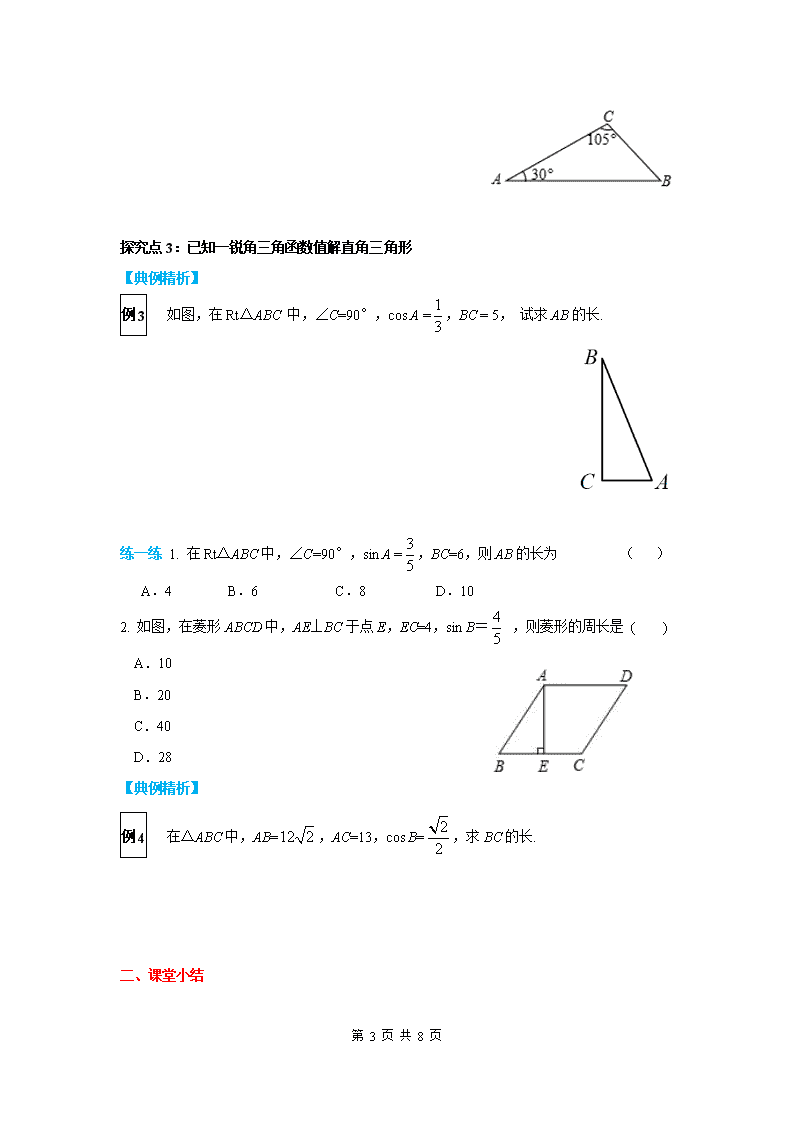如图，已知 AC = 4，求 AB 和 BC 的长． 第 3 页 共 8 页 探究点 3：已知一锐角三角函数值解直角三角形 【典例精析】 例 3 如图，在 Rt△ABC 中，∠C=90°，cos A = 1 3 ，BC = 5， 试求 AB 的长. 练一练 1. 在 Rt△ABC 中，∠C=90°，sin A = 3 5 ，BC=6，则 AB 的长为 （ ） A．4 B．6 C．8 D．10 2. 如图，在菱形 ABCD 中，AE⊥BC 于点 E，EC=4，sin B＝ 4 5 ，则菱形的周长是 ( ) A．10 B．20 C．40 D．28 【典例精析】 例 4 在△ABC 中，AB=12 2 ，AC=13，cos B= 2 2 ，求 BC 的长. 二、课堂小结 第 4 页 共 8 页 当堂检测 1. 在 Rt△ABC 中，∠C=90°，a，b，c 分别是∠A，∠B，∠C 的对边，则下列各式正确的是 ( ) A. b=a·tan A B. b=c·sin A C. b=c·cos A D. a=c·cos A 2. 如图，在 Rt△ABC 中，∠C=90°，∠B=30°，AB=8，则 BC 的长是 ( ) A. 4 3 4 B. 4 C. 8 3 D. 4 3 3. 在 Rt△ABC 中，∠C=90°，∠B=37°，BC=32，则 AC = (参考数据：sin37°≈0.60， cos37°≈0.80，tan37°≈0.75). 4.如图，已知 Rt△ABC 中，斜边 BC 上的高 AD=3，cos B= 4 5 ，则 AC 的长为 . 5.如图，在 Rt△ABC 中，∠C＝90°，AC=6， ∠BAC 的平分线 4 3AD  ，解这个直角三 角形. 第 5 页 共 8 页 6.如图，在△ABC 中，∠B=30°，∠C=45°，AC=2，求 BC 的长. 参考答案 自主学习 一、知识链接 第 6 页 共 8 页 （1）c2 90° a c b c a b 课堂探究 一、要点探究 探究点 1：已知两边解直角三角形 合作探究 解：（1） sin sin 6 sin 75 .BCA BC AB AAB  ，= = × = ´ cos cos 6 cos75 .ACA AC AB AAB  ，= = × = ´ 90 90 90 75 15 .A B B A               ， （2） 2 2 2 2 2 2 26 2.4 5.5.AB AC BC BC AB AC        ， 2.4cos cos 0.4. 66 .6 ACA A AAB        ， 90 90 90 66 24 .A B B A               ， 【典例精析】 例 1 解 6tan 3 2 BCA AC = = = ， 60A  Ð = ， 90 90 60 30B A   Ð = -Ð = - = ， 2 2 2.AB AC  练一练 解：根据勾股定理 2 2 2 230 20 10 13c a b= + = + = ， 30 3tan 1.520 2 aA b = = = = ， 56.3 .A  ∴ 90 90 56.3 33.7 .B A         ∴ 探究点 2：已知一边及一锐角解直角三角形 【典例精析】 例 2 解： 90 =90 35 =55 .A B     ∠ ∠ tan ,bB a  20 28.6.tan tan35 ba B     sin ,bB c  20 34.9.sin sin35 bc B     练一练 1.解：∵sin ,bB c  ∴ sin 14 sin 72 13.3.b c B = � 椿 ∵ cos ,aB c  ∴ cos 14 cos72 4.33.a c B = � 椿 90 72 18 .A      2. 解：如图，作 CD⊥AB 于点 D，在 Rt△ACD 中，∵∠A=30°，∴∠ACD=90°-∠A=60°， 1 2,2CD AC ∴ = 3cos 4 2 3.2AD AC A   = 在 Rt△CDB 中，∵∠DCB=∠ACB－ 第 7 页 共 8 页 ∠ACD=45°，∴BD=CD=2.∴ 2 2 2.cosBC DCB  ∠ 2 2 3.AB AD BD   ∴ 【典例精析】 例 3 解： 190 cos 3C A   ， ， 1.3 AC AB   设 1, 3AB x AC x  ， 2 2 2AB AC BC  ， 2 2 21 5 .3x x      1 2 15 2 15 2, .4 4x x    （舍去） ∴ AB 的长为15 2 .4 练一练 1.D 2.C 【典例精析】 例 4 解 ： ∵ cos B = 2 2 ， ∴ ∠ B=45 ° . 当 △ ABC 为 钝 角 三 角 形 时 ， 如 图 ① ， =12 2 =45AB B ∵ ，∠ ， = = cos 12.AD BD AB B ∴ ∵AC=13，∴由勾股定理得 CD=5.∴ BC=BD - CD=12-5=7；当△ABC 为锐角三角形时，如图②，BC=BD+CD=12+5=17.∴ BC 的 长为 7 或 17. 当堂检测 1. C 2. D 3. 24 4. 3.75 5. 解 ： ∵ 6 3cos 24 3 ACCAD AD     ， 30CAD  . ∵ AD 平 分 ∠BAC ， 60 30CAB B     ， . 12 6 3.AB BC  ， 6. 解：过点 A 作 AD⊥BC 于点 D.在△ACD 中，∠C=45°，AC=2，∴CD=AD=sin C · AC= 2sin45°= 2 .在△ABD 中，∠B=30°，∴BD= 32 6.tan 3 AD B    第 8 页 共 8 页 ∴BC=CD+BD= 2 6.