2019届高三上学期期末考试数学试题分类汇编：20 7页

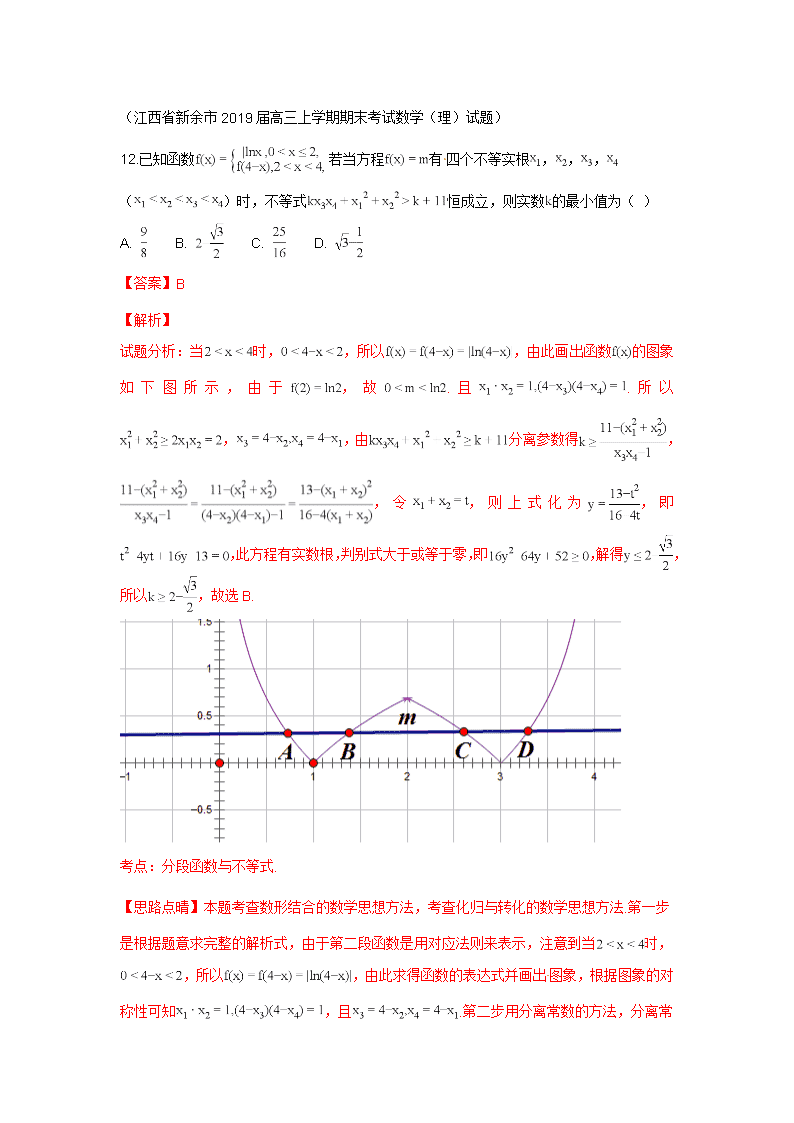
‎（江西省新余市2019届高三上学期期末考试数学（理）试题）‎ ‎12.已知函数若当方程有四个不等实根，，，（）时，不等式恒成立，则实数的最小值为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】[来源:Zxxk.Com]‎ 试题分析：当时，，所以，由此画出函数的图象如下图所示，由于，故.且.所以，，由分离参数得，，令，则上式化为，即，此方程有实数根，判别式大于或等于零，即，解得，所以，故选B.[来源:学_科_网]‎ 考点：分段函数与不等式.‎ ‎【思路点晴】本题考查数形结合的数学思想方法，考查化归与转化的数学思想方法.第一步是根据题意求完整的解析式，由于第二段函数是用对应法则来表示，注意到当时，，所以，由此求得函数的表达式并画出图象，根据图象的对称性可知，且 ‎.第二步用分离常数的方法，分离常数，然后利用求值域的方法求得的最小值.‎ ‎（湖北省宜昌市2019届高三元月调研考试文科数学试题）‎ ‎12.已知是定义域为的函数的导函数，若对任意实数都有，且有，则不等式的解集为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据条件构造函数，求函数的导数，利用函数的单调性即可得到结论 ‎【详解】不等式可化为：‎ 令，‎ ‎ ，又 ‎ 恒成立，故在R上单调递增。‎ 又，‎ ‎ 等价于，‎ 由在R上单调递增可得：，‎ 所以不等式的解集为：‎ 故选：A ‎【点睛】本题主要考查函数单调性的判断和应用，还考查了转化思想，根据条件构造函数是解决本题的关键．‎ ‎（河北省张家口市2019届高三上学期期末考试数学（文）试题）‎ ‎12.函数，则的解集为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 结合函数的解析式分三种情况：时，不等式转化为；当时，不等式转化为；当时，不等式转化为4，分别求解进而可以得到答案。‎ ‎【详解】由题意，当时，，，则，解得，与矛盾，故不成立；‎ 当时，，，则，解得，由于，故；‎ 当时，，，则4，解得，由于，故.‎ 综上的解集为.‎ 故答案为A.‎ ‎【点睛】本题考查了分段函数，考查了不等式的求解，考查了分类讨论思想的运用，属于基础题。‎ ‎（广东省清远市2019届高三上学期期末考试数学（理）试题）[来源:Z。xx。k.Com]‎ ‎10.已知，给出下列三个结论：①；②；③.中所有的正确结论的序号是（ ）‎ A. ①② B. ①③ C. ②③ D. ①②③‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 代入的特殊值，对错误序号进行排除，由此得到正确选项.‎ ‎【详解】不妨设，满足.代入验证①成立，代入②成立，代入③错误，由此排除B,C,D三个选项，本小题选A.‎ ‎【点睛】本小题主要考查利用特殊值进行实数比较大小，还考查对数的运算，属于基础题.‎ ‎（福建省厦门市2019届高三第一学期期末质检理科数学试题）‎ ‎3.实数满足，则下列不等式成立的是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由题意，指数函数是定义域R上的单调递增函数，又由，得，即可求解.‎ ‎【详解】由题意，指数函数是定义域R上的单调递增函数，‎ 又由，则，所以，故选B.‎ ‎【点睛】本题主要考查了指数函数的单调性的应用，其中解答中合理根据指数函数的单调性比较大小是解答的关键，着重考查了推理与运算能力，属于基础题.[来源:Zxxk.Com]‎ ‎（安徽省黄山市2019届高三第一次质量检测（一模）数学（理）试题）[来源:Zxxk.Com]‎ ‎11.定义域为的函数满足，则不等式的解为( )‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由，构造函数，对其求导可知，所以函数是的单调递增函数，不等式可化为，由的单调性可知，解不等式即可得到答案。‎ ‎【详解】构造函数，则，则函数是的单调递增函数，‎ 对不等式的两端同时除以得，‎ 则，解得.‎ 故答案为C.‎ ‎【点睛】由，构造增函数，是本题的一个难点，需要学生在平常的学习中多积累这样的方法。‎ ‎[来源:学科网]‎ ‎（河北省武邑中学2019届高三上学期期末考试数学（理）试题）[来源:学科网]‎ ‎16.当时，不等式恒成立，则实数a的取值范围是____．‎ ‎【答案】[来源:Zxxk.Com]‎ ‎【解析】‎ 试题分析：不等式变形为．当时，，故实数a的 取值范围是；当时，，记，，故函数递增，则，故；当时，，记，令，得或（舍去），当时，；当时，，故，则．综上所述，实数的取值范围是．‎ 考点：利用导数求函数的极值和最值．‎ ‎[来源:学科网ZXXK]‎ ‎（广东省江门市2019届高三高考模拟（第一次模拟）考试数学（理科）试题）‎ ‎5.根据市场调查，预测某种日用品从年初开始的个月内累计的需求量（单位：万件）大约是（）．据此预测，本年度内，需求量超过万件的月份是（ ）‎ A. 5月、6月 B. 6月、7月 C. 7月、8月 D. 8月、9月 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 现根据题意得到第n个月时的需求量，再由需求量大于5得到n的范围，进而得到结果.‎ ‎【详解】日用品从年初开始的个月内累计的需求量（单位：万件）大约是（）,则第个月的需求量为， ‎ 故答案为：C.[来源:学§科§网Z§X§X§K]‎ ‎【点睛】这个题目考查了数列通项的求法中已知和的关系，求表达式，一般是写出做差得通项；也考查了不含参的二次不等式的求法，较为基础.‎