【物理】2020届一轮复习人教版计算题一课时作业 4页

专练9　计算题(一)‎ ‎(时间：25分钟)‎ ‎24．(2018·合肥质检一)如图所示，水平地面上有三个质量均为m＝1 kg的小物块A、B、C，A、B间用一根轻绳水平相连．一水平恒力F作用于A上，使三物块以相同加速度运动一段时间后撤去F.已知B与C间的动摩擦因数μ1＝0.5，A和C与地面间的动摩擦因数均为μ2＝0.2，若最大静摩擦力等于滑动摩擦力，g取10 m/s2.求：‎ ‎(1)F的最大值；‎ ‎(2)从撤去F到三物块停止运动的过程中，B受到的摩擦力．‎ ‎[解析]　(1)B、C恰好要相对滑动时 对C：μ1mg－μ2(m＋m)g＝ma 解得a＝1 m/s2‎ 由题意知，A、B、C相对静止时，F有最大值Fmax 对A、B、C整体：Fmax－μ2(m＋m＋m)g＝3ma 解得Fmax＝9 N ‎(2)撤去F后，设B、C相对静止 对A、B、C整体：μ2(m＋m＋m)g＝3ma′‎ 解得a′＝2 m/s2‎ 对C：μ2(m＋m)g－fBC＝ma′‎ 解得fBC＝2 N≤fBm＝μ1mg＝5 N 故假设成立，由牛顿第三定律可知，B受到的摩擦力为2 N，方向水平向左．‎ ‎[答案]　(1)9 N　(2)2 N，方向水平向左 ‎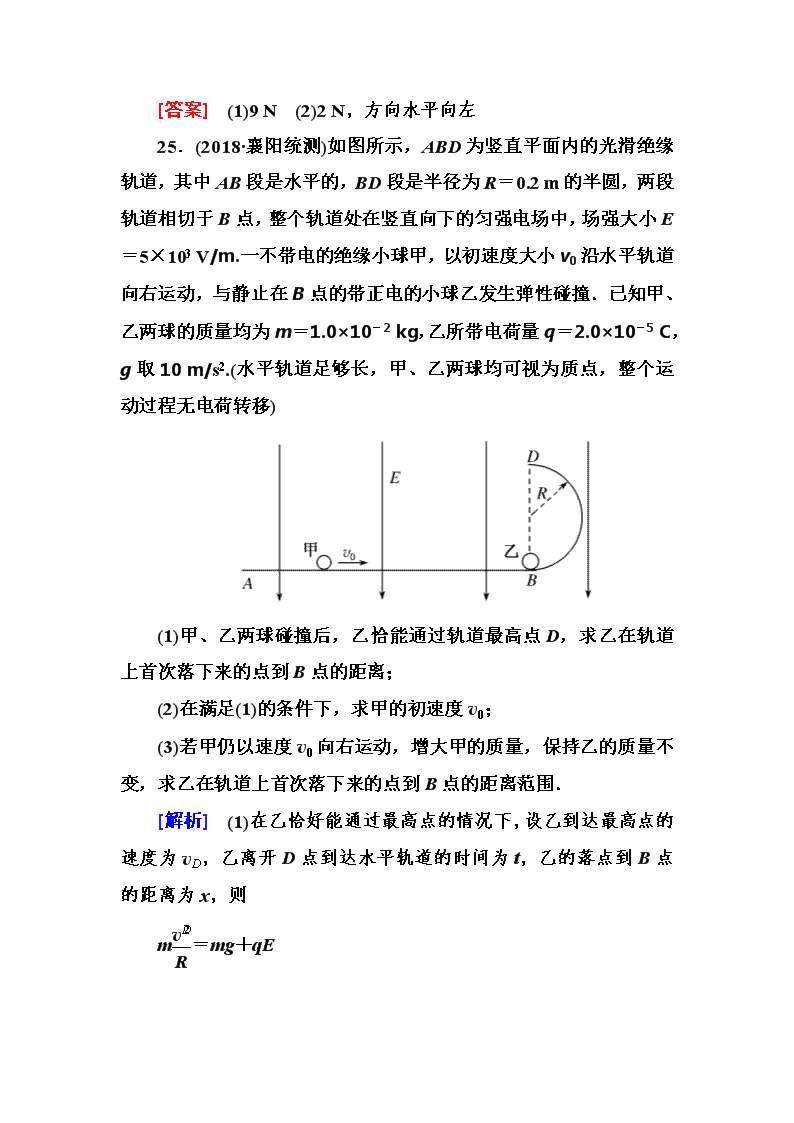25．(2018·襄阳统测)如图所示，ABD为竖直平面内的光滑绝缘轨道，其中AB段是水平的，BD段是半径为R＝0.2 m的半圆，两段轨道相切于B点，整个轨道处在竖直向下的匀强电场中，场强大小E＝5×103 V/m.一不带电的绝缘小球甲，以初速度大小v0沿水平轨道向右运动，与静止在B点的带正电的小球乙发生弹性碰撞．已知甲、乙两球的质量均为m＝1.0×10－2 kg，乙所带电荷量q＝2.0×10－5 C，g取10 m/s2.(水平轨道足够长，甲、乙两球均可视为质点，整个运动过程无电荷转移)‎ ‎(1)甲、乙两球碰撞后，乙恰能通过轨道最高点D，求乙在轨道上首次落下来的点到B点的距离；‎ ‎(2)在满足(1)的条件下，求甲的初速度v0；‎ ‎(3)若甲仍以速度v0向右运动，增大甲的质量，保持乙的质量不变，求乙在轨道上首次落下来的点到B点的距离范围．‎ ‎[解析]　(1)在乙恰好能通过最高点的情况下，设乙到达最高点的速度为vD，乙离开D点到达水平轨道的时间为t，乙的落点到B点的距离为x，则 m＝mg＋qE ‎2R＝t2‎ x＝vDt 联立解得x＝0.4 m ‎(2)设碰撞后甲、乙的速度分别为v甲、v乙，根据动量守恒定律和机械能守恒定律有：‎ mv0＝mv甲＋mv乙 mv＝mv＋mv 联立可得v乙＝v0‎ 由动能定理得，－mg·2R－qE·2R＝mv－mv 联立解得v0＝ ＝2 m/s ‎(3)设甲的质量增大为M，碰撞后甲、乙的速度分别为vM、vm，根据动量守恒定律和机械能守恒定律有 Mv0＝MvM＋mvm Mv＝Mv＋mv 联立得vm＝v0‎ 由题意知，M≥m 可得：v0≤vm<2v0‎ 设乙过D点的速度为v′D，由动能定理得 ‎－mg·2R－qE·2R＝mv′－mv 联立解得2 m/s≤v′D<8 m/s 设乙在水平轨道上首次落下的点到B点的距离为x′，则有：x′＝v′Dt 可得0.4 m≤x′<1.6 m ‎[答案]　(1)0.4 m　(2)2 m/s　(3)0.4 m≤x′<1.6 m