2018-2019学年四川省棠湖中学高二下学期期末考试数学（文）试题 Word版 11页

四川省棠湖中学2018-2019学年度高二下学期末考试 文科数学试题 本试卷共4页。考试结束后，将本试卷和答题卡一并交回。‎ 注意事项：‎ ‎1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。‎ ‎2．选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。‎ ‎3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。‎ ‎4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。‎ ‎5．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。‎ 一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1.已知集合，则（ ）‎ A. B. C. D. ‎ ‎2.已知复数，其中i为虚数单位，则 A. B. C. D. ‎ ‎3.下列函数中，既是偶函数又在上单调递增的是 A. B. C. D. ‎ ‎4.设，则“”是“”的 ‎ A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 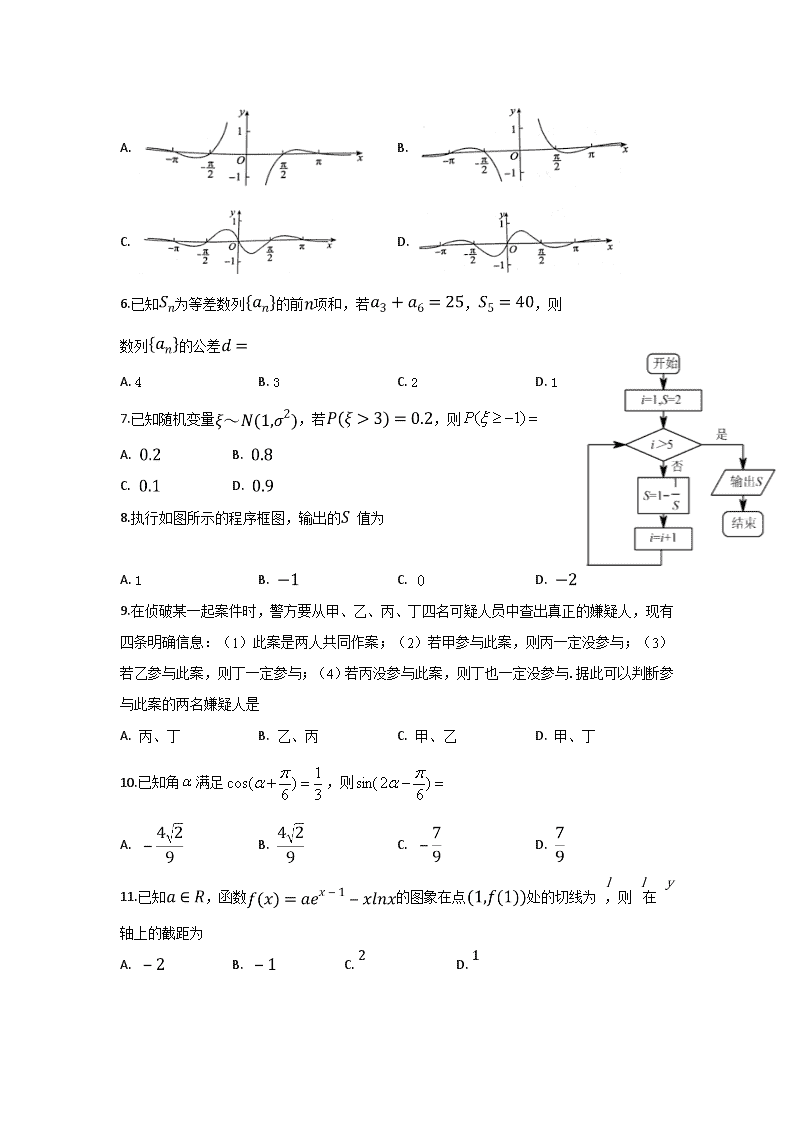既不充分也不必要条件 ‎5.函数的图象大致为 A. B. ‎ C. D. ‎ ‎6.已知为等差数列的前项和，若，，则 数列的公差 ‎ A. 4 B. ‎3 ‎C. 2 D. 1‎ ‎7.已知随机变量，若，则 A. B. ‎ C. D. ‎ ‎8.执行如图所示的程序框图，输出的 值为 A. 1 B. C. D. ‎ ‎9.在侦破某一起案件时，警方要从甲、乙、丙、丁四名可疑人员中查出真正的嫌疑人，现有四条明确信息：（1）此案是两人共同作案；（2）若甲参与此案，则丙一定没参与；（3）若乙参与此案，则丁一定参与；（4）若丙没参与此案，则丁也一定没参与.据此可以判断参与此案的两名嫌疑人是 A. 丙、丁 B. 乙、丙 C. 甲、乙 D. 甲、丁 ‎10.已知角满足，则 A. B. C. D. ‎ ‎11.已知，函数的图象在点处的切线为l，则l在y轴上的截距为 A. B. C. 2 D. 1‎ ‎12.已知为坐标原点，是双曲线的左焦点，分别为的左、右顶点，为上一点，且轴， 过点的直线与线段交于点，与轴交于点，直线与轴交于点，若，则的离心率为 A. B. C. D. ‎ 二、填空题：本题共4小题，每小题5分，共20分．‎ ‎13.已知向量=（－4，3），=（6，m），且，则m=__________.‎ ‎14.函数的最小值为___________．‎ ‎15.直三棱柱ABC-A1B‎1C1，内接于球O，且AB⊥BC，AB=3．BC=4．AA1=4，则球O的表面积______．‎ ‎16.定义在R上的奇函数满足，且在区间上，，则函数的零点的个数为___．‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．‎ ‎（一）必考题：共60分。‎ ‎17．（12分）‎ 设是各项均为正数的等比等列，且，．‎ Ⅰ求的通项公式；Ⅱ．‎ ‎18.（12分）‎ 为推动更多人阅读，联合国教科文组织确定每年的月日为“世界读书日”.设立目的是希望居住在世界各地的人，无论你是年老还是年轻，无论你是贫穷还是富裕，都能享受阅读的乐趣，都能尊重和感谢为人类文明做出过巨大贡献的思想大师们，都能保护知识产权.为了解不同年龄段居民的主要阅读方式，某校兴趣小组在全市随机调查了名居民，经统计这人中通过电子阅读与纸质阅读的人数之比为,将这 人按年龄分组，其中统计通过电子阅读的居民得到的频率分布直方图如图所示.‎ Ⅰ求的值及通过电子阅读的居民的平均年龄；‎ ‎(Ⅱ)把年龄在第组的居民称为青少年组，年龄在第组的居民称为中老年组，若选出的200人中通过纸质阅读的中老年有人，请完成上面列联表，则是否有％的把握认为阅读方式与年龄有关？‎ ‎19.（12分）‎ 在四棱锥中，平面平面，底面为矩形，，，，、分别为线段、上一点，且，.‎ Ⅰ证明：；‎ ‎(Ⅱ)证明：平面，并求三棱锥的体积.‎ ‎20.（12分）‎ 已知椭圆过点．‎ Ⅰ求椭圆的方程，并求其离心率；‎ ‎(Ⅱ)过点作轴的垂线，设点为第四象限内一点且在椭圆上（点不在直线上），点关于的对称点为，直线与交于另一点．设为原点，判断直线与直线的位置关系，并说明理由．‎ ‎21.（12分）‎ 已知函数 Ⅰ讨论的单调性；‎ Ⅱ若在上没有零点，求的取值范围．‎ ‎（二）选考题：共10分．请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分．‎ ‎22． [选修4-4：坐标系与参数方程]（10分）‎ 已知直线：（为参数），曲线（为参数）．‎ Ⅰ设与相交于，两点，求；‎ ‎(Ⅱ)若把曲线上各点的横坐标压缩为原来的倍，纵坐标压缩为原来的倍，得到曲线，设点是曲线上的一个动点，求它到直线距离的最小值．‎ ‎23．[选修4-5：不等式选讲]（10分）‎ 已知．‎ ‎(Ⅰ)当m＝－3时，求不等式的解集；‎ ‎(Ⅱ)设关于x的不等式的解集为M，且，求实数m的取值范围.‎ 四川省棠湖中学2018-2019学年度高二下学期末考试 文科数学试题答案 一．选择题 ‎1.A 2.C 3.A 4.B 5.D 6.B 7.B 8.B 9.A 10.D 11.D 12.A 二．填空题 ‎13.8. 14‎‎.. 15. 16.5‎ 三．解答题 ‎17.Ⅰ设首项为，公比为q的各项均为正数的等比等列，‎ 且，．‎ 则：，‎ 解得：，负值舍去，所以：，‎ 则：．‎ ‎（Ⅱ）由于：，‎ 所以：．‎ ‎，‎ ‎，‎ ‎．‎ ‎18.（1）由频率分布直方图可得：10×（0.01+0.015+a+0.03+0.01）＝1，解得a＝0.035，‎ 所以通过电子阅读的居民的平均年龄为：‎ ‎20×10×0.01+30×10×0.015+40×10×0.035+50×10×0.03+60×10×0.01＝41.5；‎ ‎（2）由题意人中通过电子阅读与纸质阅读的人数之比为, ∴纸质阅读的人数为200=50，其中中老年有人，∴纸质阅读的青少年有20人，电子阅读的总人数为150，‎ 青少年人数为150=90，则中老年有人，‎ 得2×2列联表，‎ 电子阅读 纸质阅读 合计 青少年（人）‎ ‎90‎ ‎20‎ ‎110‎ 中老年（人）‎ ‎60‎ ‎30‎ ‎90‎ 合计（人）‎ ‎150‎ ‎50‎ ‎200‎ 计算，‎ 所以有的把握认为认为阅读方式与年龄有关．‎ ‎19.（1）∵AM＝AD＝3，MD＝3，‎ ‎∴AM2+AD2＝MD2，∴AM⊥AD，‎ ‎∵平面MAD⊥平面ABCD，平面MAD∩平面ABCD＝AD，‎ ‎∴AM⊥平面ABCD，‎ 又BD⊂平面ABCD，∴AM⊥BD．‎ ‎（2）在棱AD上取一点N，使得ND＝1，‎ ‎∵CE＝1，∴CE＝ND，又BC∥AD，‎ ‎∴ECND，又AB∥CD，∴EN∥AB，‎ ‎∵＝，∴FN∥AM，‎ ‎∵FN∩EN＝N，∴平面ENF∥平面MAB，又EF⊂平面ENF，‎ ‎∴EF∥平面MAB，‎ ‎∵AM⊥平面ABCD，且FD＝MD，AM＝3，‎ ‎∴F到平面ABCD的距离d＝，‎ ‎∴VD﹣AEF＝VF﹣ADE＝＝1．‎ ‎20.解：（1）由椭圆方程椭圆过点，可得．‎ ‎∴，‎ ‎∴椭圆的方程为，离心率．‎ ‎（2）直线与直线平行．证明如下：‎ 设直线，，‎ 设点的坐标为，，‎ 由得，‎ ‎∴，∴，同理，‎ ‎∴，‎ 由，，有，‎ ‎∵在第四象限，∴，且不在直线上．∴，‎ 又，故，∴直线与直线平行．‎ ‎21.Ⅰ，‎ 令，解得；‎ 令，解得，‎ 函数的单调增区间为，单调减区间为 Ⅱ要使在上没有零点，‎ 只需在上或，‎ 又，只需在区间上，．‎ 当时，在区间上单调递减，‎ 则，‎ 解得与矛盾．‎ 当时，在区间上单调递减，在区间上单调递增，‎ ‎，‎ 解得，‎ ‎，‎ 当时，在区间上单调递增，‎ ‎，满足题意，‎ 综上所述，实数a的取值范围是： ．‎ ‎22.解：（1）直线的普通方程为，的普通方程．‎ 联立方程组，解得与的交点为，，则．‎ ‎（2）曲线的参数方程为（为参数），故点的坐标为，‎ 从而点到直线的距离是，‎ 由此当时，取得最小值，且最小值为．‎ ‎23.（1）当时，‎ 原不等式等价于 故有或或 解得：或或 综上，原不等式的解集 ‎（2）由题意知在上恒成立，‎ 即在上恒成立 所以 即在上恒成立 所以 即在上恒成立 由于，‎ 所以，即的取值范围是