- 1.03 MB
- 2021-04-15 发布
2019—2020学年高考质量监测考试
高三数学(理)试题
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答题前,考生务必将自己的姓名、准考证号、考场号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结束后,将答题卡交回.
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,,则( )
A. B. C. D.
2.已知复数,则( )
A. B. C. D.
3.已知,,,则a,b,c的大小关系是( )
A. B. C. D.
4.已知中,则“”是“是直角三角形”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.若过抛物线焦点的直线与抛物线交于A、B两点(不重合,则(O为坐标原点)的值是( )
A.-3 B. C.3 D.
6.《聊斋志异》中有:“挑水砍柴不堪苦,请归但求穿墙术”.在数学中,我们称形如以下形式的等式具有“穿墙术”:,,,则按照以上规律,若具有“穿墙术”,则,满足的关系式为( )
A. B. C. D.
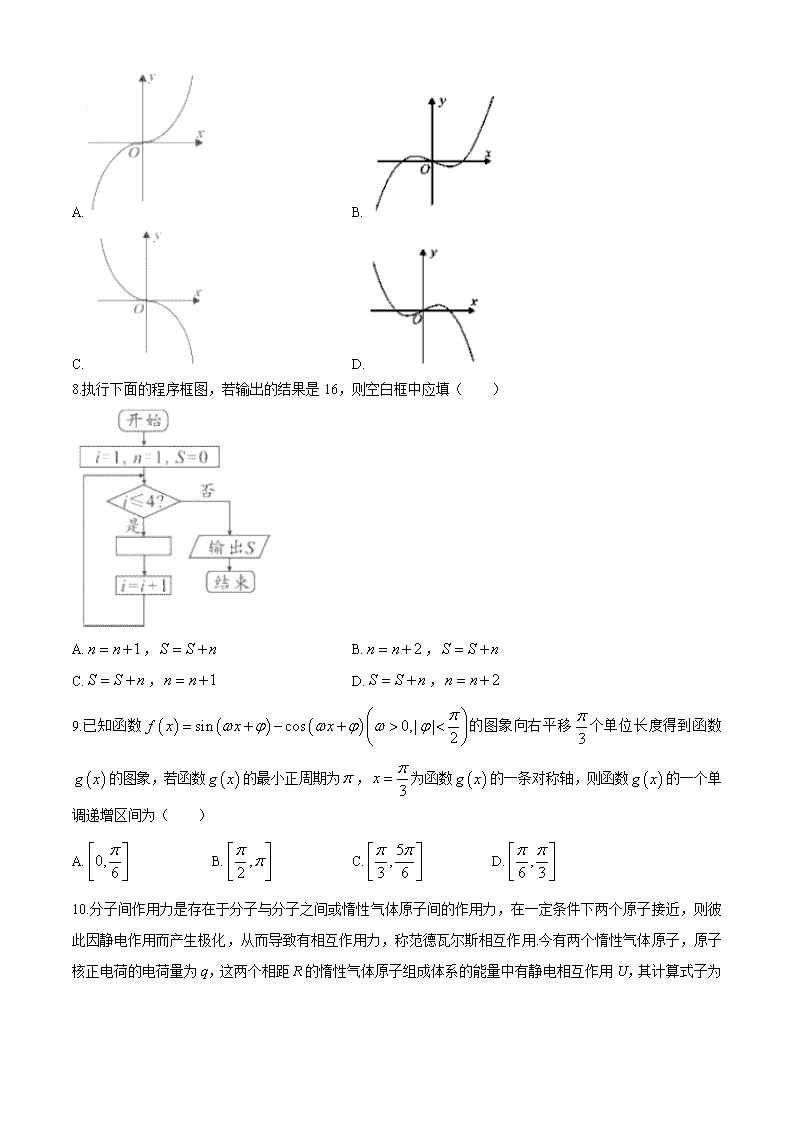
7.已知函数,若是的导函数,则函数的图象大致是( )
A. B.
C. D.
8.执行下面的程序框图,若输出的结果是16,则空白框中应填( )
A., B.,
C., D.,
9.已知函数的图象向右平移个单位长度得到函数的图象,若函数的最小正周期为,为函数的一条对称轴,则函数的一个单调递增区间为( )
A. B. C. D.
10.分子间作用力是存在于分子与分子之间或惰性气体原子间的作用力,在一定条件下两个原子接近,则彼此因静电作用而产生极化,从而导致有相互作用力,称范德瓦尔斯相互作用.今有两个惰性气体原子,原子核正电荷的电荷量为q,这两个相距R的惰性气体原子组成体系的能量中有静电相互作用U,其计算式子为
,其中,为静电常量,、分别表示两个原子的负电中心相对各自原子核的位移.已知,,,且,则的近似值为( )
A. B. C. D.
11.过双曲线的右焦点的直线在第一、第四象限交两渐近线分别于P,Q两点,且,O为坐标原点,若内切圆的半径为,则该双曲线的离心率为( )
A. B. C. D.
12.设函数恰有两个极值点,则实数t的取值范围是( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.己知向量,的夹角余弦值为,则_______________.
14.若,则函数在区间内单调递增的概率是____________.
15.的展开式中项的系数是____________.(用数字作答)
16.已知四棱锥中,底面是梯形,且,,,,,,的中点为E,则四棱锥外接球的表面积为_______________.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知数列的前n项和,数列是等差数列,且.
(1)求数列的通项公式;
(2)令,求数列的前n项和.
18.(本小题满分12分)
《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑(bie nao)指四个面均为直角三角形的四面体.如图在堑堵中,.
(1)求证:四棱锥为阳马;
(2)若,当鳖臑体积最大时,求锐二面角的余弦值.
19.(本小题满分12分)
设椭圆的离心率为,椭圆C上一点P到左右两个焦点,的距离之和是4.
(1)求椭圆的方程;
(2)已知过的直线与椭圆C交于A,B两点,且两点与左右顶点不重合,若,求四边形面积的最大值.
20.(本小题满分12分)
在全面抗击新冠肺炎(OVID-19)疫情的特殊时期,市教育局提出“停课不停学”的口号,鼓励学生进行线上学习.某位高中数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取了45名学生进行跟踪问卷.其中每周线上学习数学时间不少于5小时的有19
人,余下的人中,在检测考试中数学平均成绩不足120分的占,统计成绩后得到如下2×2列联表:
分数不少于120分
分数不足120分
合计
线上学习时间不少于5小时
4
19
线上学习时间不足5小时
合计
45
(1)请完成上面的2×2列联表,并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)①按照分层抽样的方法,在上述样本中从分数不少于120分和分数不足120分的两组学生中抽取9名学生,设抽到不足120分且每周线上学习时间不足5小时的人数是X,求X的分布列(概率用组合数进行表示);
②若将频率视为概率,从全校高三该次检测数学成绩不少于120分的学生中随机抽取20人,求这些人中每周线上学习时间不少于5小时的人数Y的期望和方差.
附:临界值表
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:,其中.
21.(本小题满分12分)
已知函数,.
(1)当时,求曲线在点处的切线方程;
(2)求函数在上的极值;
(3)设函数,若,且对任意的实数,不等式恒成立(e是自然对数的底数),求实数a的取值范围.
【选考题】请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.作答时,请用2B铅笔在答题卡上把所选题目对应的题号涂黑.
22.(本小题满分10分)【选修4-4:坐标系与参数方程】
在平面直角坐标系中,曲线的参数方程为(为参数,)以原点为极点,x
轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求曲线、的直角坐标方程;
(2)设P、Q分别为、上的动点,若P、Q间距离的最小值为,求实数m的值.
23.(本小题满分10分)【选修4-5:不等式选讲】
已知正实数x,y满足.
(1)解关于x的不等式;
(2)证明:.
2019-2020学年高考质量监测考试
高三数学(理)参考答案
一、选择题(本大题共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
A
D
A
D
A
D
C
D
B
C
1.,,∴.
2.,故.
3.因为,
,故.
4.若,则或,不能推出是直角三角形;若,则,所以是直角三角形也不能推出;故“”是“是直角三角形”的既不充分也不必要条件.
5.抛物线为,焦点为,设,,,由
有,所以,,故.
6.由题可知:,,,
可归纳:,所以.
7.∵,∴,∴,所以单调递增,由于;故当时,;当时,.
8.A选项,若空白处是,时,成立,,,成立,所以,,成立,所以,,成立,所以,,不成立,故,不符合题意;B选项,若空白处是,时,成立,,,成立,所以,,成立,所以,,成立,所以,,不成立,故,不符合题意;C选项,若空白处是,时,成立,,成立,所以,,成立,所以,,成立,所以,,不成立,故,不符合题意;D选项,若空白处是,时,成立,,,成立,所以,,成立,所以,,成立,所以,,不成立,故,符合题意.
9.由题意知,所以,因为的最小正周期为,所以,解得,所以,由为的一条对称轴,则,,即,,因为,可得,所以函数,令,解得,,当时,.
10.
11.如图,设的内切圆圆心为M,则M在x轴上,
过点M分别作于N,于T,由得四边形为正方形,由焦点到渐近线的距离为b,得,又,所以,
由,得,所以,
故.
12.因为,.因为恰有两个极值点,所以恰有两个不同的解,显然是其一解,另一解由方程来确定,且此解不等于1.令,则,故函数在上单调递增,从而,且.所以,当且时,函数恰有两个极值点,即实数的取值范围是.
二、填空题(本大题共4小题,每小题5分,共20分)
13.1 14. 15.300 16.
【解析】
13.由题意有,即,解得或,验证不成立.
14.∵函数在区间内单调递增,∴,
在恒成立,∴在恒成立,∴,又因为,∴,
所以函数在区间内单调递增的概率是.
15.展开式的通项为,,由题意,令,得;令,得.故的展开式中,常数项为,含项为,所以的展开式中项系数为.
16.
【解析】由题得,,,又,∴四边形是正方形,,,平面,又∵,∴平面,所以.则有,即,解得.
∵球心O到B,C,D,E四点距离相等,设O在平面的投影为H,
那么,,,,设,则有,,,,
又∵,∴.
∵是正方形,∴平面且到B,C,D,E四点距离相等的点即为正方形的对称中心,即对角线的交点,则.
∴.过P作于F,∵平面,
∴,,∴平面,即F是点P在平面的投影.
∵是等边三角形,∴,,
∴,与联立解得,则.故答案为:.
三、解答题(本大题共6小题,共70分)
17.【解析】
(1)由题意知,当时,,
又当时,,经检验当时适合上式,所以.………………3分
设数列的公差为d,由,即,
可解得,,所以.…………………………6分
(2)由(1)知,又,得
,
,
两式作差,得
,
所以.…………………………12分
18.【解析】
(1)∵底面,面,∴.
又,,∴面,
又四边形为矩形,∴四棱锥为阳马.……………………3分
(2)∵,,∴,又∵底面,且
∴,
当且仅当时,取最大值.……………………9分
∵,底面,
∴以A为原点,建立如图所示空间直角坐标系,
则,,,.
,,.
设平面的一个法向量.,由,得,
同理得平面的一个法向量.
∴,所以锐二面角的余弦值为.………………12分
19.【解析】
(1)依题意,,,
因为,所以,,
所以椭圆C方程为.…………………………3分
(2)设,,设直线为:,
则由,消去x可得:,
即,其中,
,
因为,所以四边形是平行四边形,
设平面四边形的面积为S,
则,.…………9分
设,则,
所以,因为,所以,所以,
所以四边形面积的最大值为6.…………………………12分
20.【解析】
(1)
分数不少于120分
分数不足120分
合计
线上学习时间不少于5小时
15
4
19
线上学习时间不足5小时
10
16
26
合计
25
20
45
∵,
∴有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”.………………5分
(2)①由分层抽样知,需要从不足120分的学生中抽取人,
X的可能取值为0,1,2,3,4,
,,,
,.
所以,X的分布列:
0
1
2
3
4
②从全校不少于120分的学生中随机抽取1人,此人每周上线时间不少于5小时的概率为,设从全校不少于120分的学生中随机抽取20人,这些人中每周线上学习时间不少于5小时的人数为Y,则,
故,.…………………………12分
21.【解析】
(1)当时,,,所以,,所以曲线在点处的切线方程为.……………………2分
(2),
①当时,,在上单调增,所以无极值;
②当时,令,得,列表如下:
0
极小值
所以的极小值为.
综上所述,当时,无极值;
当时,的极小值为,无极大值.…………………………6分
(3)因为.
由题意,对任意的,恒成立,所以,
解得,又,所以.…………………………8分
①当时,因为,所以,当且仅当时,取等号.
由(2)知,在上单调增,所以.
所以,当且仅当时,取等号,
所以在上单调增,则,
解得,此时,.
②当时,由(2)知,在上单调递增,且,
又,所以存在,且,使得,
即,得.
所以的解为和,列表如下:
0
0
极大值
极小值
所以,即
又,所以恒成立,此时,.
综上所述,实数a的取值范围为.……………………12分
22.【解析】
(1)消去参数可得的直角坐标方程为:,
的方程即:,即,
即的直角坐标方程为:.…………………………4分
(2)设,,
则Q到的距离,又.
由P、Q间距离的最小值为知:
当时,不符合题意;
当时,得;
当时,,得.
综上,或.…………………………10分
23.【解析】
(1)因为,且,,
∴可化为:,即,
又即,可解得,所以不等式的解集为.…………5分
(2)证明一:因为,且,,∴
.
当且仅当时,等号成立.…………………………10分
证明二:因为,且,,∴
,当且仅当时,等号成立.……………………10分