山东省东营市2012届高三上学期期末考试数学（理）试题 11页

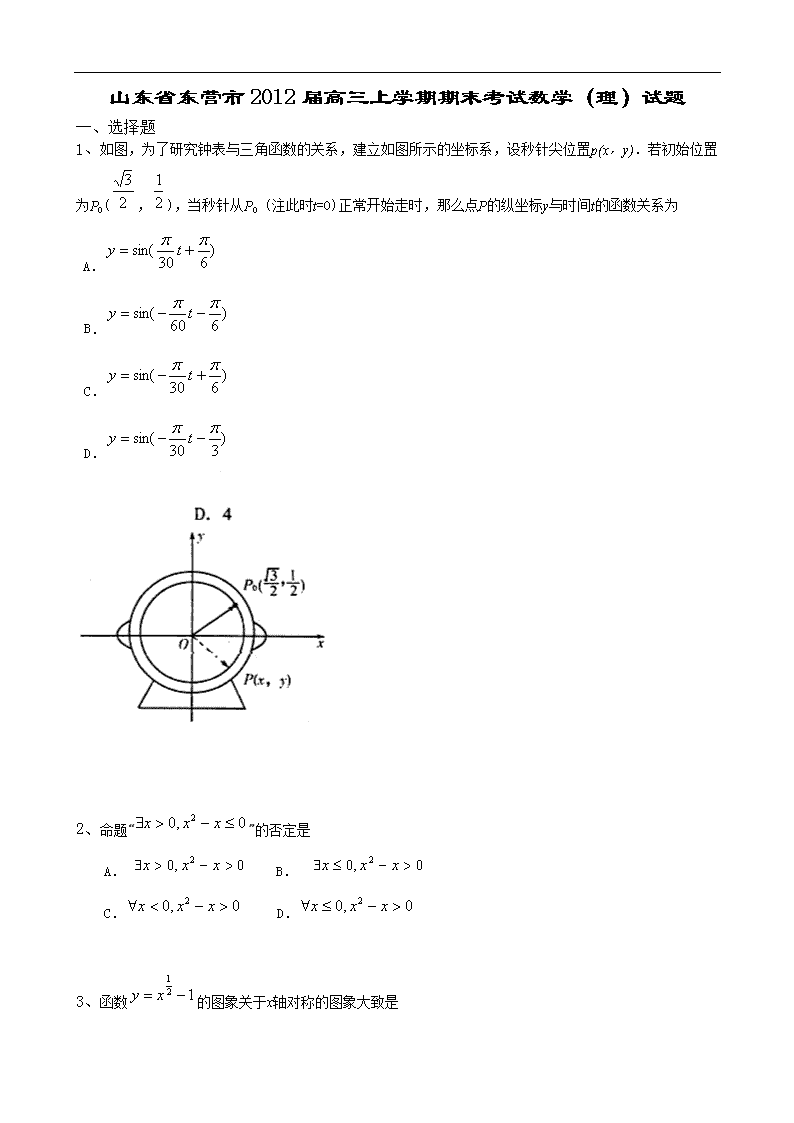
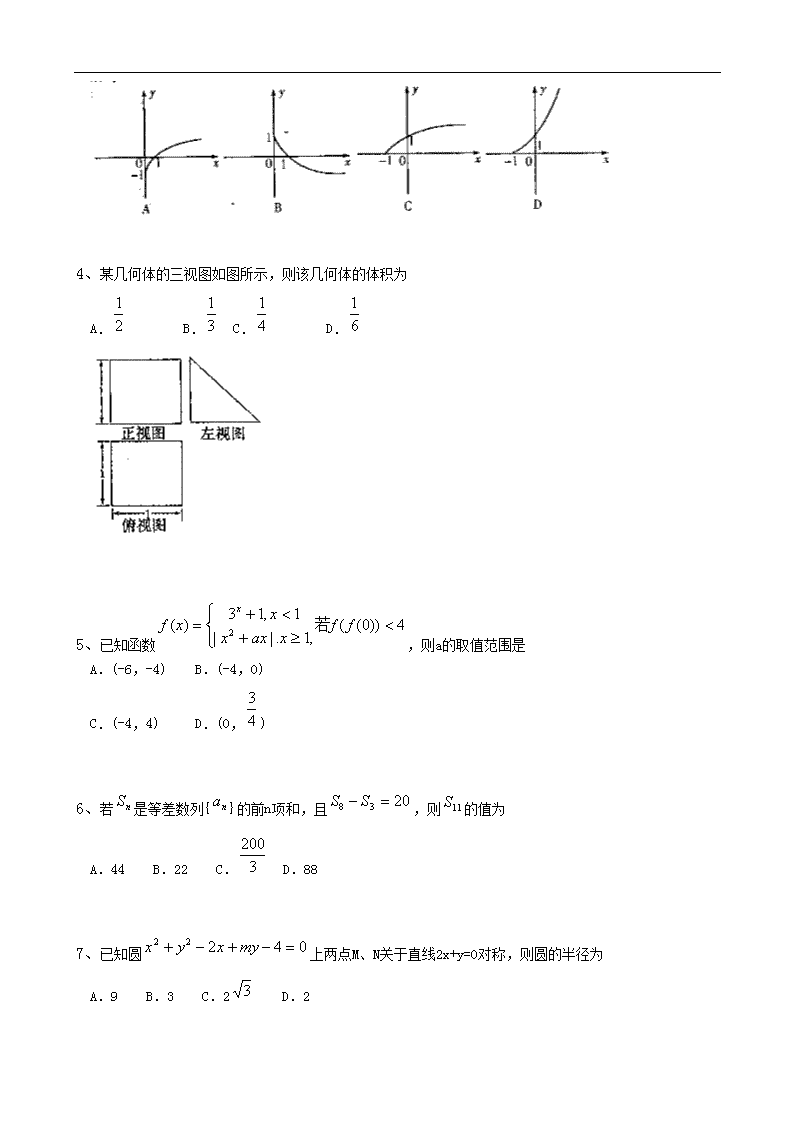
山东省东营市2012届高三上学期期末考试数学（理）试题 一、选择题 ‎1、如图，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位置p(x，y)．若初始位置为P0(，)，当秒针从P0 (注此时t=0)正常开始走时，那么点P的纵坐标y与时间t的函数关系为 ‎ A．‎ B．‎ C．‎ D．‎ ‎2、命题“”的否定是 ‎ A． B． ‎ ‎ C． D．‎ ‎3、函数的图象关于x轴对称的图象大致是 ‎4、某几何体的三视图如图所示，则该几何体的体积为 ‎ A． B． C． D．‎ ‎5、已知函数，则a的取值范围是 ‎ A．(-6，-4) B．(-4，0)‎ ‎ C．(-4，4) D．(0，)‎ ‎6、若是等差数列{}的前n项和，且，则的值为 ‎ ‎ A．44 B．‎22 C． D．88‎ ‎7、已知圆上两点M、N关于直线2x+y=0对称，则圆的半径为 ‎ A．9 B．‎3 C．2 D．2‎ ‎8、已知关于x,y的不等式组，所表示的平面区域的面积为l6，则k的值为 ‎ A． -l B．‎0 C． 1 D． 3‎ ‎9、函数 (e为自然对数的底数)在区间[-1，1]上的最大值是 ‎ A． B．‎1 C．e+1 D．e-1‎ ‎10、已知全集，集合，则CuP等于 A．[ B. ()‎ ‎ C．(0,+∞) D．(-∞，0] [，+∞)‎ ‎11、偶函数满足，且在x∈[0，1]时, ，则关于x的方程，在x∈[0，3]上解的个数是 ‎ A． 1 B．‎2 C.3 D.4‎ ‎12、已知点P是抛物线上一点，设P到此抛物线准线的距离是d1，到直线的距离是d2，则dl+d2的最小值是 ‎ ‎ A. B. C. D．3 ‎ 二、填空题 ‎13、已知向量a，b满足|a|=2，|b|=1，a与b的夹角为60 0，则|a-2b|等于 .‎ ‎14、小明爸爸开车以‎80km/h 的速度沿着正北方向的公路行驶，小明坐在车里向外观察，在点A处望见电视塔P在北偏东300方向上，15分钟后到点B处望见电视塔在北偏东750方向上，则汽车在点B时与电视塔P的距离是 km．‎ ‎15、已知双曲线的离心率为，焦距为‎2c，且‎2a2=‎3c，双曲线 上一点P满足,则 ．‎ ‎16、设m、n,是两条不同的直线，是两个不同的平面，给出下列四个命题，‎ ‎ ①若m⊥n,m⊥，，则；‎ ‎ ②若；‎ ‎ ③若； ‎ ‎ ④若.‎ 其中正确命题的序号是 (把所有正确命题的序号都写上)．‎ 三、解答题 ‎17、‎ ‎ 已知定义在实数集上的函数，其导函数记为，且满足 其中为常数，．设函数.‎ ‎ (I)求实数a的值；‎ ‎ (Ⅱ)若函数无极值点，其导函数有零点，求m的值；‎ ‎(Ш)求函数在x∈[0，a]的图象上任一点处的切线斜率k的最大值．‎ ‎18、‎ ‎ 已知函数 ‎ (I)化简函数的解析式，并求其定义域和单调区间；‎ ‎ (Ⅱ)若，求的值．‎ ‎19、如图所示，直角梯形ACDE与等腰直角ABC所在平面互相垂直，F为BC的中点，，AE∥CD，DC=AC=2AE=2．‎ ‎ (I)求证：AF//平面BDE； ‎ ‎ (Ⅱ)求二面角B-DE-C的余弦值．‎ ‎20、‎ ‎ 设等比数列{}的前n项和为，已知 ‎ ‎ (I)求数列{}的通项公式；‎ ‎(Ⅱ)在与之间插人n个数，使这n+2个数组成公差为的等差数列，求数列{}的前n项和．‎ ‎21、‎ ‎ 某工厂生产一种产品的成本费共由三部分组成：①原材料费每件50元；②职工工资支出7500+20x元；③电力与机器保养等费用为戈元：其中x是该厂生产这种产品的总件数．‎ ‎ (I)把每件产品的成本费p(x)(元)表示成产品件数x的函数，并求每件产品的最低成本费； ‎ ‎ (Ⅱ)如果该厂生产的这种产品的数量x不超过170件且能全部销售，根据市场调查，每件产品的销售价为Q(x)(元)，且Q(x)=1240-．试问生产多少件产品，总利润最高?并求出最高总利润．(总利润=总销售额-总的成本) ‎ ‎22、‎ ‎ 如图，椭圆G的中心在坐标原点，其中一个焦点为圆F：的圆心，右顶点是圆F与x轴的一个交点．已知椭圆G与直线l：相交于A、B两点．‎ ‎ (I)求椭圆的方程；‎ ‎ (Ⅱ)求AOB面积的最大值．‎ 以下是答案 一、选择题 ‎1、 C ‎2、 D ‎3、 B ‎4、 A ‎5、 B ‎6、 A ‎7、 B ‎8、 C ‎9、 D ‎10、 A ‎11、 D ‎12、 C 二、填空题 ‎13、 2‎ ‎14、 ‎ ‎15、 4‎ ‎16、 ①④‎ 三、解答题 ‎17、‎ ‎ ‎ ‎18、‎ ‎ ‎ ‎19、‎ ‎20、‎ ‎21、‎ ‎22、‎