- 1.21 MB
- 2021-04-15 发布
浙江省2020届高三数学一轮复习典型题专项训练
函数
一、选择、填空题
1、(温州市2019届高三8月适应性测试)已知,则_________.=________.
2、(金丽衢十二校2019届高三第一次联考)偶函数f (x)满足f (x一1)=f(x+1),且当x [0,1]时,f (x)=x,则f()=__ 若在区间[1,3]内,函数g(x)=f (x)-kx一k有4个零点,则实数k的取值范围是_.
3、(浙江省名校协作体2019届高三上学期第一次联考)已知,函数,记的最小值为,则( )
A. 在上是增函数,在上是减函数
B. 在上是减函数,在上是增函数
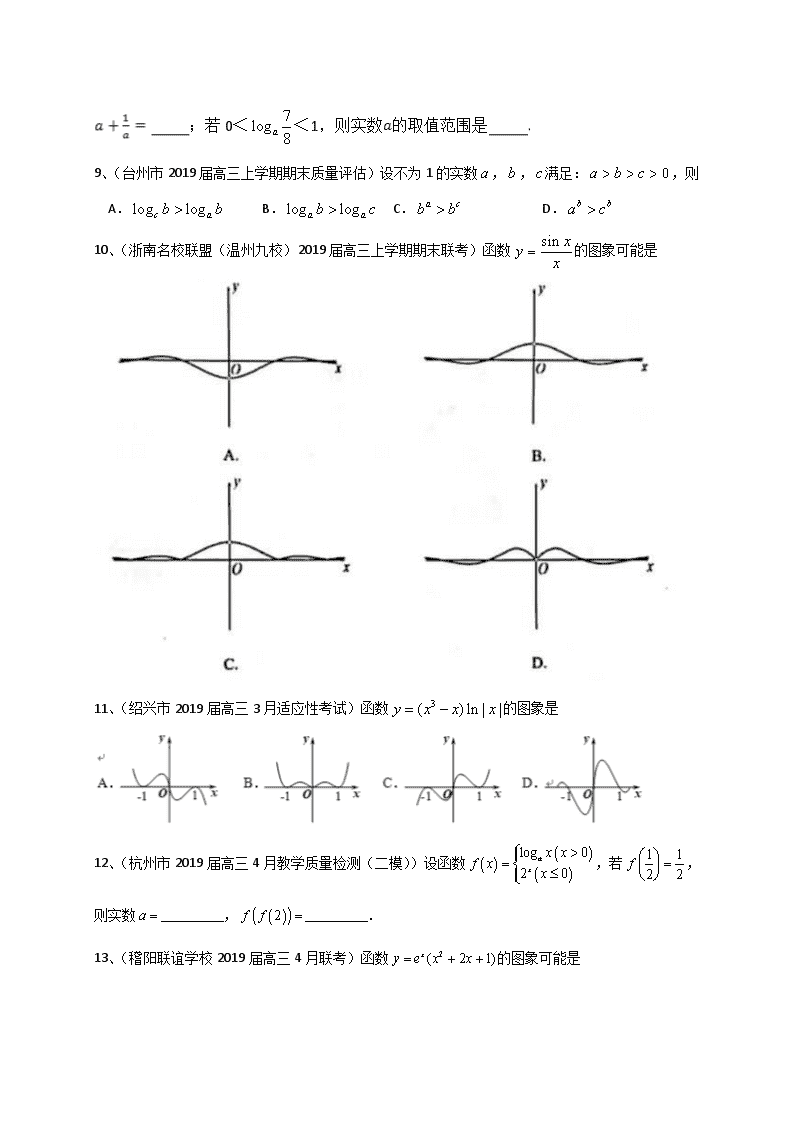
C. 在R上是奇函数
D. 在R上是偶函数
4、(七彩阳光联盟2019届高三上学期期初联考)已知函数,且,则实数的取值范围是( )
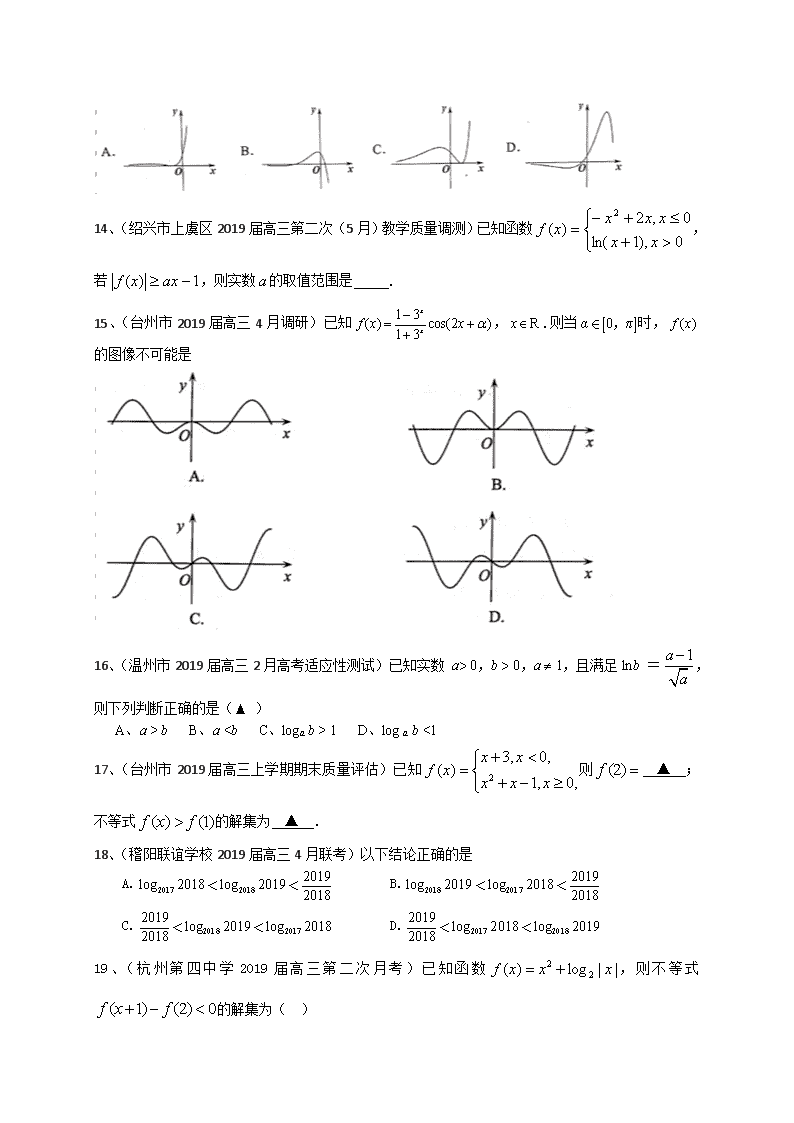
A. B. C. D.
5、(温州九校2019届高三第一次联考)若,则________,________
6、(嘉兴市2019届高三上学期期末检测)函数 f (x) = (x + 1)ln(| x - 1|)的大致图象是
7、(丽水、衢州、湖州三地市2019届高三上学期期末)已知a,b∈R,f(x)=ex﹣ax+b,
若f(x)≥1恒成立,则的取值范围是
8、(宁波市2019届高三上学期期末考试)已知实数且若=2,则
;若0<<1,则实数的取值范围是
9、(台州市2019届高三上学期期末质量评估)设不为1的实数,,满足:,则
A. B. C. D.
10、(浙南名校联盟(温州九校)2019届高三上学期期末联考)函数的图象可能是
11、(绍兴市2019届高三3月适应性考试)函数的图象是
12、(杭州市2019届高三4月教学质量检测(二模))设函数,若,则实数 , .
13、(稽阳联谊学校2019届高三4月联考)函数的图象可能是
14、(绍兴市上虞区2019届高三第二次(5月)教学质量调测)已知函数,若,则实数的取值范围是 .
15、(台州市2019届高三4月调研)已知,.则当时,的图像不可能是
16、(温州市2019届高三2月高考适应性测试)已知实数 a> 0,b > 0,a ¹ 1,且满足lnb =,则下列判断正确的是(▲ )
A、a > b B、a 1 D、log a b <1
17、(台州市2019届高三上学期期末质量评估)已知则 ▲ ;不等式的解集为 ▲ .
18、(稽阳联谊学校2019届高三4月联考)以下结论正确的是
A. B.
C. D.
19、(杭州第四中学2019届高三第二次月考)已知函数,则不等式的解集为( )
A. B.
C. D.
20、(杭州第四中学2019届高三第二次月考)已知,则_________,_________
21、(浙江省名校协作体2019届高三2月联考)函数 f (x) = (x2 - 2)ln|x|的图像为 ( ▲ )
22、(七彩阳光联盟2019届高三下学期第三次联考)函数,则 ,若存在四个不同的实数a,b,c,d,使得,则abcd的取值范围为 .
参考答案:
1、27,1 2、, 3、D 4、D 5、,
6、B 7、[-1,+ 8、 9、D 10、B
11、C 12、 13、A
14、 15、A 16、C
17、; 18、B 19、C 20、0、3
21、B 22、1,[0,1)
二、解答题
1、(杭州第四中学2019届高三第二次月考)已知函数
(1) 当且是上的增函数,求实数的取值范围;
(2) 当,且对任意实数,关于的方程总有三个不相等的实数根,求实数的取值范围;
2、(杭州市第二中学2020届高三上学期开学考试)已知函数是定义在上的奇函数,当时,.
(1)求在上的解析式;
(2)若,函数,是否存在实数使得的最小值为,若存在,
求的值;若不存在,说明理由.
3、(杭州第四中学2019届高三第一次月考)已知函数和的图象关于原点对称,且
。
(1)求函数的解析式;
(2)解不等式
4、已知函数,设在上的最大值为,
(Ⅰ)求的表达式;
(Ⅱ)是否存在实数,使得的定义域为,值域为?如果存在,求出的值;如果不存在,请说明理由.
5、已知函数是定义在上的偶函数,当时,.现已画出函数在轴左侧的图象,如图所示.
(Ⅰ)画出函数在轴右侧的图象,并写出函数在上的单调递增区间;
(Ⅱ)求函数在上的解析式.
6、设函数.
(1)当时,证明:函数不是奇函数;
(2)设函数是奇函数,求与的值;
(3)在(2)条件下,判断并证明函数的单调性,并求不等式的解集.
参考答案:
1、(1);(2)
2、
3、
4、解:(Ⅰ)因为函数图象的对称轴为, 1分
所以当,即时,; 3分
当,即时,. 5分
所以 6分
(Ⅱ)假设存在符合题意的实数,则
由(Ⅰ)可知,当时,. 8分
所以若,有,则. 9分
所以,且为单调递增函数. 11分
所以 12分
所以 13分
5、解:(Ⅰ)图略; 3分
函数的单调增区间为和; 6分
(Ⅱ)设,则. 7分
因为函数是定义在上的偶函数,且当时,,
所以. 10分
所以 13分
6、解:(1)当时,
所以,,所以,所以函数不是奇函数.
(2)由函数是奇函数,得,
即对定义域内任意实数都成立,化简整理得
对定义域内任意实数都成立
所以,所以或
经检验符合题意.
(3)由(2)可知
易判断为R上的减函数,证明略(定义法或导数法)
由,不等式即为,由在R上的减函数可得.
另解:由得,即,解得,所以.