2018届二轮复习三角恒等变换与解三角形课件（全国通用） 38页

第 2 讲　三角恒等变换与解三角形 - 2 - 热点考题诠释 高考方向解读 1 . (2017 山东 , 理 9) 在 △ ABC 中 , 角 A , B , C 的对边分别为 a , b , c , 若 △ ABC 为锐角三角形 , 且满足 sin B (1 + 2cos C ) = 2sin A cos C+ cos A sin C , 则下列等式成立的是 ( 　　 ) A. a= 2 b B. b= 2 a C. A= 2 B D. B= 2 A 答案 解析 解析 关闭 ∵ sin B (1 + 2cos C ) = 2sin A cos C+ cos A sin C , ∴ sin B+ 2sin B cos C= (sin A cos C+ cos A sin C ) + sin A cos C , ∴ sin B+ 2sin B cos C= sin B+ sin A cos C , ∴ 2sin B cos C= sin A cos C , 又 △ ABC 为锐角三角形 , ∴ 2sin B= sin A , 由正弦定理 , 得 a= 2 b. 故选 A . 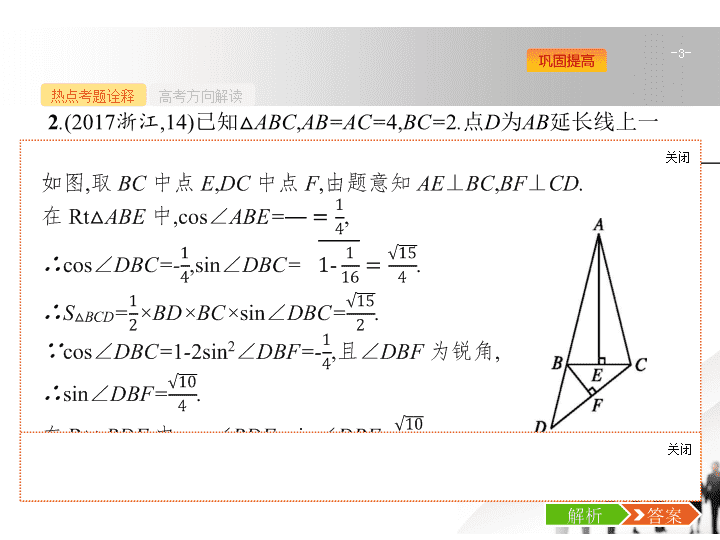答案 解析 关闭 A - 3 - 热点考题诠释 高考方向解读 2 . (2017 浙江 ,14) 已知 △ ABC , AB=AC= 4, BC= 2 . 点 D 为 AB 延长线上一点 , BD= 2, 连接 CD , 则 △ BDC 的面积是 　　　　　 ,cos ∠ BDC= 　　　　　 .   答案 解析 解析 关闭 答案 解析 关闭 - 4 - 热点考题诠释 高考方向解读 - 5 - 热点考题诠释 高考方向解读 - 6 - 热点考题诠释 高考方向解读 - 7 - 热点考题诠释 高考方向解读 - 8 - 热点考题诠释 高考方向解读 5 . (2017 全国 2, 理 17) △ ABC 的内角 A , B , C 的对边分别为 a , b , c. 已知 sin( A+C ) = 8sin 2 . (1) 求 cos B ; (2) 若 a+c= 6, △ ABC 的面积为 2, 求 b. - 9 - 热点考题诠释 高考方向解读 - 10 - 热点考题诠释 高考方向解读 本部分主要考查三角函数的基本公式、三角恒等变换及解三角形等基本知识 . 三角函数与解三角形相结合或三角函数与平面向量相结合是考向的主要趋势 , 试题难度为中低档 . 三角恒等变换是高考的热点内容 , 主要考查利用各种三角函数进行求值与化简 , 其中降幂公式、辅助角公式是考查的重点 , 切化弦、角的变换是常考的三角变换思想 . 正弦定理、余弦定理以及解三角形问题是高考的必考内容 , 主要考查 : ① 边和角的计算 ; ② 三角形形状的判断 ; ③ 面积的计算 ; ④ 有关的范围问题 . 考向预测 : 三角恒等变换和解三角形综合的问题是浙江高考主要考查方式 , 以考查三角恒等变换公式、正余弦定理公式和面积公式为主 . 这部分内容是解答题常考题型 , 但从 2017 年高考和样卷角度来看目前这部分内容以填空题形式出现 ,2018 年很可能延续这种风格 . - 11 - 命题热点一 命题 热点二 命题 热点三 - 12 - 命题热点一 命题 热点二 命题 热点三 - 13 - 命题热点一 命题 热点二 命题 热点三 - 14 - 命题热点一 命题 热点二 命题 热点三 规律方法 1 . 三角恒等变换求值时应注意下列问题 : 当 “ 已知角 ” 有两个时 , 一般把 “ 所求角 ” 表示为两个 “ 已知角 ” 的和或差的形式 ; 当 “ 已知角 ” 有一个时 , 此时应着眼于 “ 所求角 ” 与 “ 已知角 ” 的和或差的关系 , 然后应用诱导公式把 “ 所求角 ” 变成 “ 已知角 ” . - 15 - 命题热点一 命题 热点二 命题 热点三 答案 解析 解析 关闭 答案 解析 关闭 - 16 - 命题热点一 命题 热点二 命题 热点三 答案 答案 关闭 - 17 - 命题 热点一 命题热点二 命题 热点三 - 18 - 命题 热点一 命题热点二 命题 热点三 ( 2) ① 证明 : 由正弦定理得 sin B+ sin C= 2sin A cos B , 故 2sin A cos B= sin B+ sin( A+B ) = sin B+ sin A cos B+ cos A sin B. 于是 sin B= sin( A-B ) . 又 A , B ∈ (0, π ), 故 0