2020九年级数学上册 第3章 圆的基本性质阶段性测试（六）练习 （新版）浙教版 6页

阶 段 性 测 试(六)‎ ‎(见学生单册)‎ ‎[考查范围：圆的基本性质(3.6～3.8)]‎ 一、选择题(每小题5分，共30分)‎ ‎1．已知扇形的圆心角为120°，半径为‎3 cm，那么扇形的面积为(　A　)‎ A．3π cm2 B．π cm‎2 ‎ C．6π cm2 D．2π cm2‎ ‎2．如果一个扇形的弧长是，半径是3，那么此扇形的圆心角为(　D　)‎ A．40° B．45° C．60° D．80°‎ ‎3．圆内接四边形ABCD中，若∠A∶∠B∶∠C＝1∶2∶5，则∠D等于(　B　)‎ A．60° B．120° C．140° D．150°‎ 第4题图 ‎4．如图所示，圆上有A，B，C，D四点，其中∠BAD＝80°.若圆的半径为‎18 cm，则弧BAD的长为(　D　)‎ A．10π cm 　　 B．15π cm C．16π cm 　　 D．20π cm ‎5．圆内接正六边形的边长与该边所对的劣弧的长的比是(　C　)‎ A．1∶ B．1∶π C．3∶π D．6∶π 6‎ 第6题图 ‎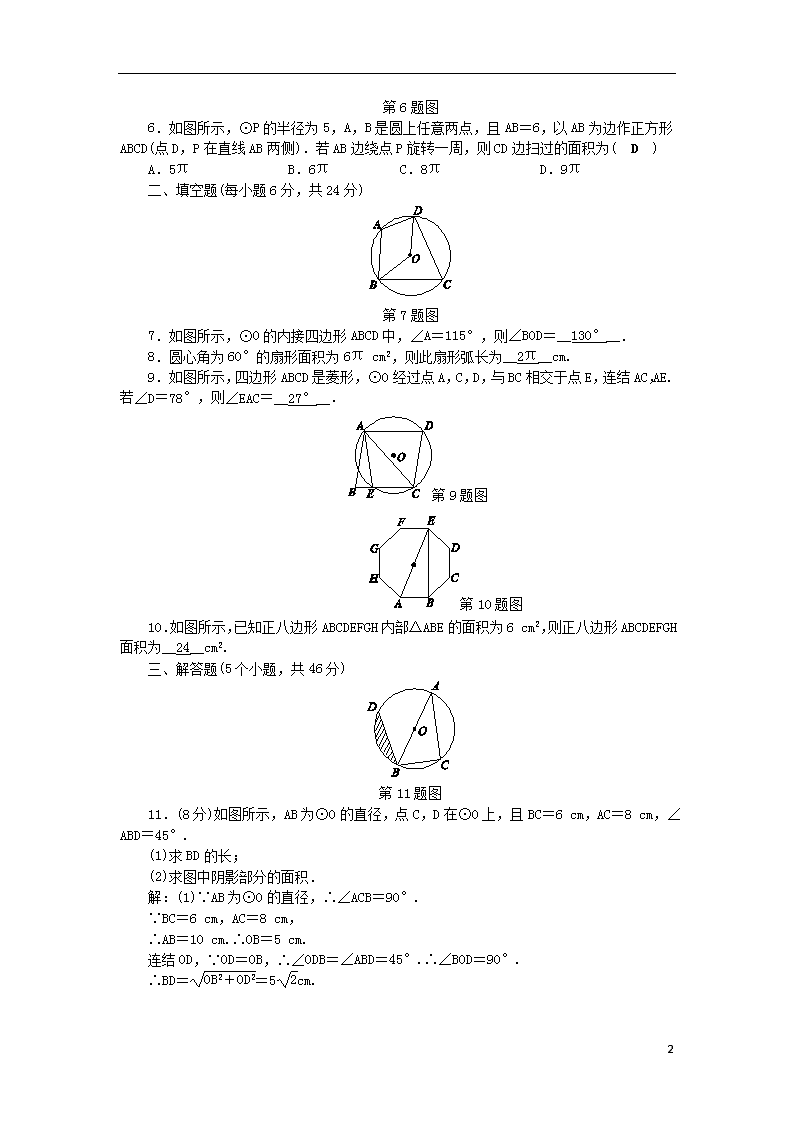6．如图所示，⊙P的半径为5，A，B是圆上任意两点，且AB＝6，以AB为边作正方形ABCD(点D，P在直线AB两侧)．若AB边绕点P旋转一周，则CD边扫过的面积为(　D　)‎ A．5π B．6π C．8π D．9π 二、填空题(每小题6分，共24分)‎ 第7题图 ‎7．如图所示，⊙O的内接四边形ABCD中，∠A＝115°，则∠BOD＝__130°__．‎ ‎8．圆心角为60°的扇形面积为6π cm2，则此扇形弧长为__2π__cm.‎ ‎9．如图所示，四边形ABCD是菱形，⊙O经过点A，C，D，与BC相交于点E，连结AC，AE.若∠D＝78°，则∠EAC＝__27°__．‎ ‎　第9题图 ‎　　　　　第10题图 ‎10．如图所示，已知正八边形ABCDEFGH内部△ABE的面积为‎6 cm2，则正八边形ABCDEFGH面积为__24__cm2.‎ 三、解答题(5个小题，共46分)‎ 第11题图 ‎11．(8分)如图所示，AB为⊙O的直径，点C，D在⊙O上，且BC＝‎6 cm，AC＝‎8 cm，∠ABD＝45°.‎ ‎(1)求BD的长；‎ ‎(2)求图中阴影部分的面积．‎ 解：(1)∵AB为⊙O的直径，∴∠ACB＝90°.‎ ‎∵BC＝6 cm，AC＝8 cm，‎ ‎∴AB＝10 cm.∴OB＝5 cm. ‎ 连结OD，∵OD＝OB，∴∠ODB＝∠ABD＝45°.∴∠BOD＝90°.‎ ‎∴BD＝＝5cm. 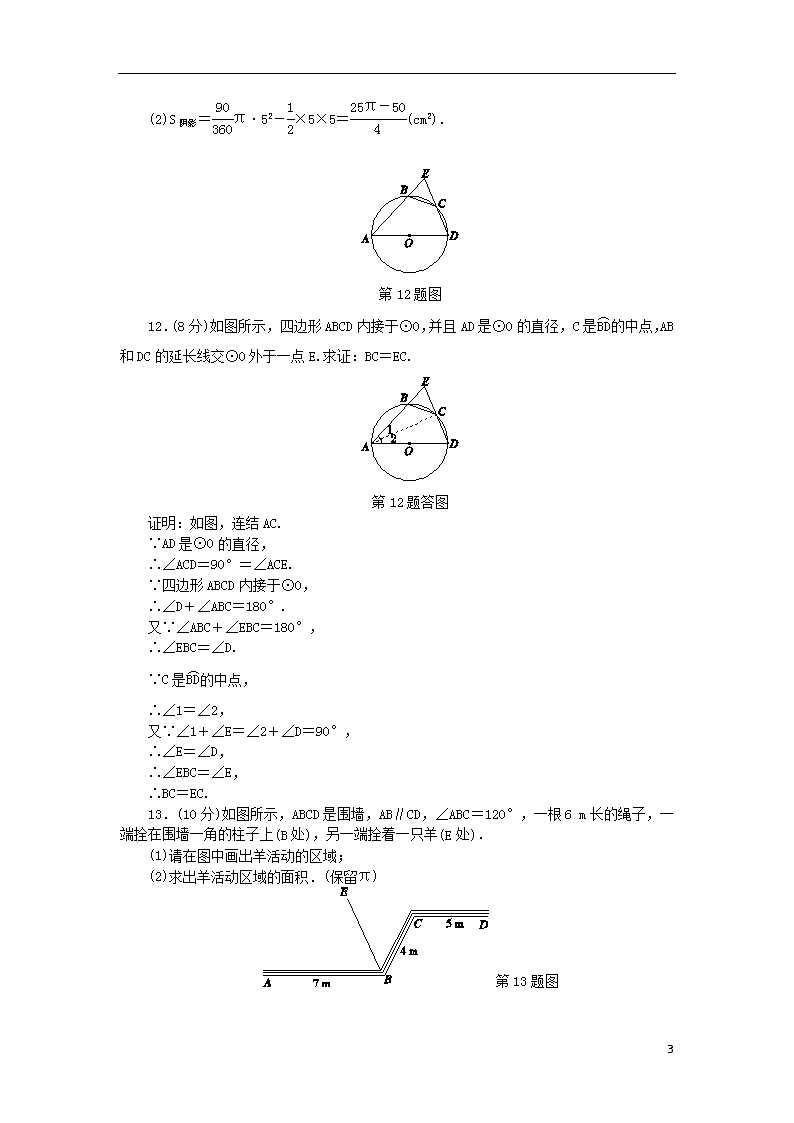‎ 6‎ ‎(2)S阴影＝π·52－×5×5＝(cm2)．‎ 第12题图 ‎12．(8分)如图所示，四边形ABCD内接于⊙O，并且AD是⊙O的直径，C是的中点，AB和DC的延长线交⊙O外于一点E.求证：BC＝EC.‎ 第12题答图 证明：如图，连结AC.‎ ‎∵AD是⊙O的直径，‎ ‎∴∠ACD＝90°＝∠ACE.‎ ‎∵四边形ABCD内接于⊙O，‎ ‎∴∠D＋∠ABC＝180°.‎ 又∵∠ABC＋∠EBC＝180°，‎ ‎∴∠EBC＝∠D.‎ ‎∵C是的中点，‎ ‎∴∠1＝∠2，‎ 又∵∠1＋∠E＝∠2＋∠D＝90°，‎ ‎∴∠E＝∠D，‎ ‎∴∠EBC＝∠E，‎ ‎∴BC＝EC.‎ ‎13．(10分)如图所示，ABCD是围墙，AB∥CD，∠ABC＝120°，一根‎6 m长的绳子，一端拴在围墙一角的柱子上(B处)，另一端拴着一只羊(E处)．‎ ‎(1)请在图中画出羊活动的区域；‎ ‎(2)求出羊活动区域的面积．(保留π)‎ 第13题图 6‎ 解：(1)如图所示，扇形BFG和扇形CGH为羊活动的区域．‎ 第13题答图 ‎(2)S扇形GBF＝＝12 π m2，‎ S扇形HCG＝＝π m2，‎ ‎∴羊活动区域的面积为：12π＋π＝π m2.‎ 第14题图 ‎14．(10分)如图所示，在⊙O中，弦BC垂直于半径OA，垂足为E，D是优弧上一点，连结BD，AD，OC，∠ADB＝30°.‎ ‎(1)求∠AOC的度数；‎ ‎(2)若弦BC＝‎6 cm，求图中劣弧的长．‎ 第14题答图 解：(1)如图，连结OB.‎ ‎∵弦BC垂直于半径OA，‎ ‎∴BE＝CE，＝.‎ 又∵∠ADB＝30°，‎ ‎∴∠AOC＝∠AOB＝2∠ADB＝60°.‎ ‎(2)∵BC＝6，∴CE＝BC＝3.‎ 在Rt△OCE中，∠AOC＝60°，∴∠OCE＝30°，‎ 6‎ ‎∴OE＝OC.‎ ‎∵OE2＋CE2＝OC2，‎ ‎∴＋32＝OC2，∴OC＝2.‎ ‎∵＝，‎ ‎∴∠BOC＝2∠AOC＝120°，‎ ‎∴的长＝＝＝π(cm)．‎ ‎15．(10分)如图1正方形ABCD内接于⊙O，E为CD任意一点，连结DE，AE.‎ ‎(1)求∠AED的度数；‎ ‎(2)如图2，过点B作BF∥DE交⊙O于点F，连结AF，AF＝1，AE＝4，求DE的长度．‎ 第15题图 第15题答图 解：(1)如图1中，连结OA，OD.‎ ‎∵四边形ABCD是正方形，‎ ‎∴∠AOD＝90°，‎ ‎∴∠AED＝∠AOD＝45°.‎ ‎(2)如图2中，连结CF，CE，CA，作DH⊥AE于H.‎ 第15题答图 ‎∵BF∥DE，AB∥CD，‎ ‎∴∠ABF＝∠CDE，‎ ‎∵∠CFA＝∠AEC＝90°，‎ ‎∴∠DEC＝∠AFB＝135°，‎ ‎∵CD＝AB，‎ ‎∴△CDE≌△ABF，‎ ‎∴AF＝CE＝1，∴AC＝＝，‎ 6‎ ‎∴AD＝AC＝，‎ ‎∵∠DHE＝90°，∴∠HDE＝∠HED＝45°，‎ ‎∴DH＝HE，设DH＝EH＝x，‎ 在Rt△ADH中，∵AD2＝AH2＋DH2，‎ ‎∴＝(4－x)2＋x2，解得x＝或，‎ ‎∴DE＝DH＝或.‎ 6‎