- 872.00 KB
- 2021-04-15 发布
邯郸市2016~2017学年度第一学期期末教学质量检测
高二数学(理科)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
2.考试时间120分钟,满分150分.
3.答题前,考生务必将自己的姓名、准考证号填写在答题卡相应的位置.
4.全部答案在答题卡上完成,答在本试卷上无效.
第Ⅰ卷(选择题 共60分)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.不等式的解集为( )
A.或 B.或
C.或 D.或
2.曲线在点处的切线方程为( )
A. B. C. D.
3.双曲线的一个焦点到渐近线的距离为( )
A.1 B. C. D. 2
4.在空间直角坐标系中,,,三点到坐标分别为,,,若,则( )
A.3 B.1 C. D.-3
5.在中,若,则的形状是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.不能确定
6.在等差数列中,,,则( )
A.9 B.9.5 C.10 D.11
7.命题“,使得”的否定是( )
A.,使得 B.,使得
C.,使得 D.,使得
8.在正方体中,,分别为和的中点,则异面直线与所成角的余弦值为( )
A.0 B. C. D.
9.在平面直角坐标系中,已知顶点、,直线与直线的斜率之积为-2,则动点的轨迹方程为( )
A. B.()
C. D.()
10.已知实数,满足如果目标函数的最小值为-2,则实数等于( )
A.0 B.-2 C.-4 D.1
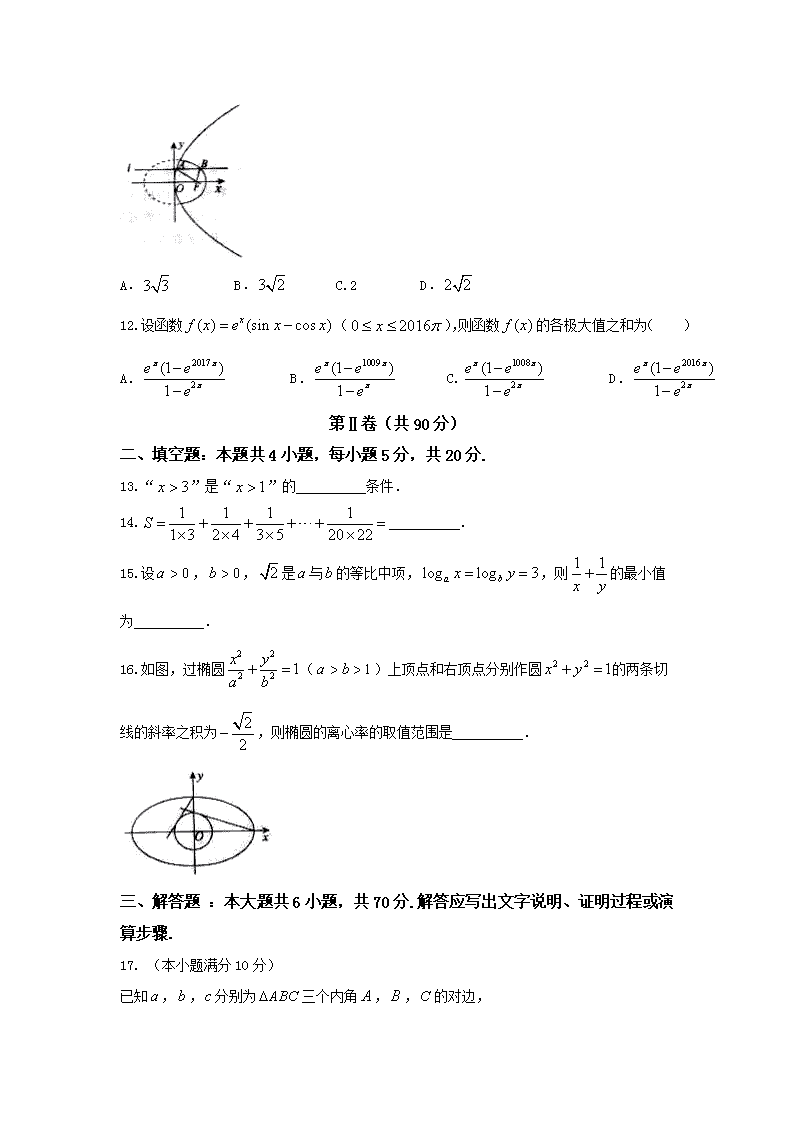
11.如图,动直线:与抛物线交于点,与椭圆交于抛物线右侧的点,为抛物线的焦点,则的最大值为( )
A. B. C.2 D.
12.设函数(),则函数的各极大值之和为( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本题共4小题,每小题5分,共20分.
13.“”是“”的 条件.
14. .
15.设,,是与的等比中项,,则的最小值为 .
16.如图,过椭圆()上顶点和右顶点分别作圆的两条切线的斜率之积为,则椭圆的离心率的取值范围是 .
三、解答题 :本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. (本小题满分10分)
已知,,分别为三个内角,,的对边,
.
(Ⅰ)求;
(Ⅱ)若,求的面积的最大值.
18. (本小题满分12分)
数列的前项和记为,,().
(Ⅰ)求的通项公式;
(Ⅱ)求数列的前项和.
19. (本小题满分12分)
如图四棱锥中,四边形为平行四边形,为等边三角形,是以为直角的等腰直角三角形,且.
(Ⅰ)证明:平面平面;
(Ⅱ)求二面角的余弦值.
20. (本小题满分12分)
某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为,半径为,不计厚度,单位:米),按计划容积为立方米,且,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为千元.
(Ⅰ)求关于的函数关系,并求其定义域;
(Ⅱ)求建造费用最小时的.
21. (本小题满分12分)
在平面直角坐标系中,已知圆:的圆心为,圆:的圆心为,一动圆与圆内切,与圆外切.
(Ⅰ)求动圆圆心的轨迹方程;
(Ⅱ)过点的直线与曲线交于,两点,若,求直线的方程.
22. (本小题满分12分)
已知函数,
(Ⅰ)求函数的单调区间;
(Ⅱ)若函数有两个零点,,证明.
高二数学(理科)参考答案及评分标准
一、选择题
1-5:CDCCA 6-10:BBDBC 11、12:DD
二、填空题
13.充分/充分不必要 14. 15. 16.
三、解答题
17.(本小题满分10分)
解:(Ⅰ)由正弦定理,得
…………………………1分
………………………………………………………2分
………………………………………………………………4分
.………………………………………………………………………………5分
(Ⅱ)三角形的面积,……………………………………………………………6分
由余弦定理,得,…………………………………………………8分
又,所以,当且仅当时等号成立.
所以,面积的最大值为.…………………………………………………………………………10分
18.(本小题满分12分)
解:(Ⅰ)由,(),①
(),②……………………………………………………………………………………2分
①-②,得().………………………………………………………………4分
又由,得
.………………………………………………………………………………5分
所以( 1),数列是以2为首项,2为公比的等比数列,故.……………………6分
(Ⅱ)由(Ⅰ),得
,③
,④…………………………………………………………8分
③-④,得.………………………………………………………………10分
所以.………………………………………………………………………………………12分
19.(本小题满分12分)
解:(Ⅰ)设为的中点,连接与,
则 ,.……………………………………………………………………………………1分
设,则,,
,………………………………………………………………………………………3分
,所以,
故平面平面.………………………………………………………………………………………4分
(Ⅱ)由(Ⅰ)可知,,两两互相垂直.的方向为轴正方向,为单位长,以为坐标原点,建立如图所示空间直角坐标系,则,,,,,所以,,,,,…………………………………………………………………………8分
设是平面的法向量,则即所以,
设是平面的法向量,则同理可取,………………………………10分
则,所以二面角的余弦值为.…………………………………12分
20.(本小题满分12分)
解:(Ⅰ)由容积为立方米,得.…………………………………………………2分
,解得,…………………………………………………………………………4分
又圆柱的侧面积为,
所以建造费用,定义域为.…………………………………………………………6分
(Ⅱ),………………………………………………………………8分
又,所以,所以建造费用,在定义域上单调递减,所以当时建造费用最小.……………………………………………………………………………………………………12分
21.(本小题满分12分)
解:(Ⅰ)设动圆的半径为,则.
两式相加,得,……………………………………………………………………2分
由椭圆定义知,点的轨迹是以、为焦点,焦距为2,实轴长为4的椭圆,其方程为
.……………………………………………………………………………………………………4分
(Ⅱ)当直线的斜率不存在时,直线的方程为,则,,
.……………………………………………………………………………………………6分
当直线的斜率存在时,设直线的方程为,设,,联立
消去,得,则有,,……………………8分
.…10分
由已知,得,解得.
故直线的方程为.……………………………………………………………………………12分
22.(本小题满分12分)
解:(Ⅰ),……………………………………………………2分
,当时,;当时,.
所以函数在上单调递增.…………………………………………………………………………4分
(Ⅱ),,不妨设,又由(Ⅰ)可知,.
,又函数在上单调递减,所以等价于,即.………………………………………………………………………………………6分
又,而,
所以
,………………………………………………………8分
设,则.…………………………………………………10分
当时,而,故当时,.
而恒成立,
所以当时,,
故.…………………………………………………………………………………………………12分