- 2.06 MB
- 2021-04-15 发布
铁人中学2018级高二学年·下学期期中考试
数学(文科)试题
试题说明:1、本试题满分150分,答题时间120分钟。
2、请将答案填写在答题卡上,考试结束后只交答题卡。
第Ⅰ卷 选择题部分
一、选择题(每小题只有一个选项正确,每小题5分,共60分。)
1.已知集合,则( )
A. B. C. D.
2.已知命题,则命题为( )
A. B.
C. D.
3.三个数,,的大小顺序为( )
A. B. C. D.
4.下列命题错误的是( )
A.命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2≠0”
B.若p:∀x≥0,,则¬p:∃x0≥0,
C.若复合命题:“p∧q”为假命题,则p,q均为假命题
D.“x>2”是x2﹣3x+2>0”的充分不必要条件
5.设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
6.已知定义在上的奇函数满足,且当时,,则( )
A. B. C. D.
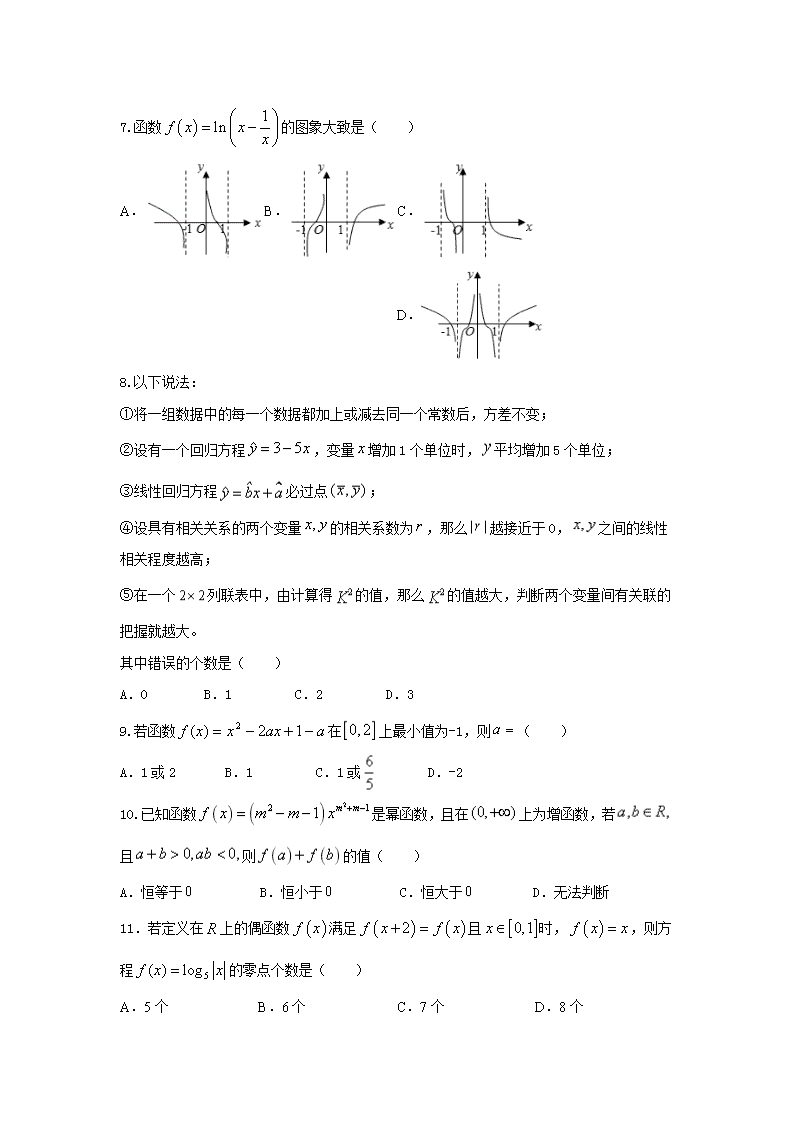
7.函数的图象大致是( )
A.B.C. D.
8.以下说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个回归方程,变量增加1个单位时,平均增加5个单位;
③线性回归方程必过点;
④设具有相关关系的两个变量的相关系数为,那么越接近于0,之间的线性相关程度越高;
⑤在一个列联表中,由计算得的值,那么的值越大,判断两个变量间有关联的把握就越大。
其中错误的个数是( )
A.0 B.1 C.2 D.3
9.若函数在上最小值为-1,则( )
A.1或2 B.1 C.1或 D.-2
10.已知函数是幂函数,且在上为增函数,若且则的值( )
A.恒等于 B.恒小于 C.恒大于 D.无法判断
11.若定义在上的偶函数满足且时,,则方程的零点个数是( )
A.5个 B.6个 C.7个 D.8个
12.已知,且,若函数在上是增函数,则实数的取值范围为( )
A. B. C. D.
第Ⅱ卷 非选择题部分
二、填空题(每小题5分,共20分)
13.函数的单调递增区间为 .
14.曲线在点处的切线的方程为__________.
15.是函数为偶函数的______条件.
(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
16.设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),已知当x∈[0,1]时,,则
①2是函数f(x)的一个周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④x=1是函数f(x)的一个对称轴;
其中所有正确命题的序号是
三、解答题(共70分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)计算:
(1)
(2)
18.(12分)已知命题p:满足,命题q:,若p∨q为真,p∧q为假,求的取值范围.
19.(12分)为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动
不喜好体育运动
男生
5
女生
10
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明你的理由;
(3)在上述喜好体育运动的6人中随机抽取两人,求恰好抽到一男一女的概率.
参考公式:.
独立性检验临界值表:
0.10
0.05
0.025
0.010
2.706
3.841
5.024
6.635
20.(12分)已知函数为定义在R上的奇函数,当时,.
(1)求的值;
(2)用函数单调性的定义证明:函数在上单调递增;
(3)求函数在上的解析式.
21.(12分)已知斜率为1的直线与椭圆交于P,Q两点,且线段PQ的中点为,椭圆C的上顶点为.
(1)求椭圆C的离心率;
(2)设直线与椭圆C交于M,N两点,若直线BM与BN的斜率之和为2,证明:过定点.
22.(12分)已知函数(是自然对数的底数).
(1)求证:;
(2)若不等式在上恒成立,求正实数的取值范围.
铁人中学2018级高二学年下学期期中考试
数学试题(文)答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
B
D
C
A
A
B
C
B
C
D
B
二、填空题
13. 14.. 15.充要 16.①②④
三、解答题
17. (1)10 (2)2
18.【答案】m≤﹣2或2≤m<5
若p真:,即:;
若q真:,
, ;
∵p∨q为真,p∧q为假,
∴①当p真q假时:或,即或;
②当p假q真时:,即;
∴综上得:或.
19.【答案】(1)列联表见解析;(2)能,理由见解析;(3).
(1)喜好体育运动的人数为:,
列联表补充如下:
喜好体育运动
不喜好体育运动
男生
20
5
女生
10
15
(2)∵.
∴能在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关.
(3)6人中有男生4人,设为,,,,女生2人,设为,,
随机抽取两人所有的情况为:,,,,,,,,,,,,,,,共15种.
其中一男一女包含8种情况,故概率为.
20.【答案】(1)(2)证明见解析(3)
(1)因为当时,
所以
又因为为奇函数,所以
(2),
则
因为,所以;因为,所以
所以,即
所以函数在上单调递增
(3)当时,
所以
又因为
所以函数在上的解析式为:
21.【答案】(1)(2)见证明
【详解】(1)设点,,由于点为线段的中点
所以,
又两式作差,
所以,即;
(2)由(1)结合上顶点,椭圆的方程为,
设点,
联立得,则韦达定理得,
据题意可得
代入韦达定理得,化简得,
所以直线为,过定点,
综上,直线过定点.
22.【答案】(1)证明见解析;(2)
(1),可得,
当,解得,
∴当时,为增函数,
当时,为减函数,
的最小值为.
.
(2)∵不等式在上恒成立,
在上恒成立,
即在上恒成立.
令,
,当时,解得,
∴当时,为减函数,
当时,为增函数,
的最小值为,
∴,
则正数的取值范围为.