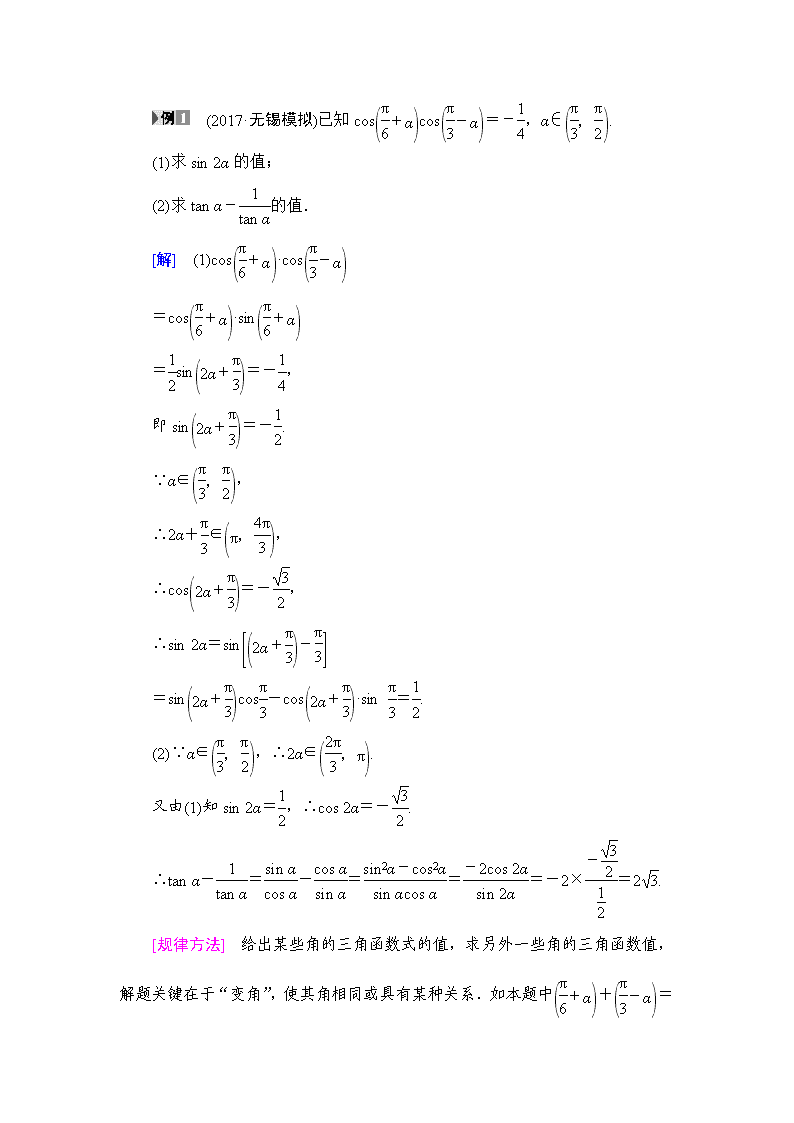- 291.00 KB
- 2021-04-15 发布
第24课 二倍角的三角函数
[最新考纲]
内容
要求
A
B
C
二倍角的正弦、余弦及正切
√
1.二倍角的正弦、余弦、正切公式
(1)sin 2α=2sin αcos α;
(2)cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α;
(3)tan 2α=.
2.二倍角公式的变形及逆用
(1)公式C2α的变形:
①sin2α=(1-cos 2α);
②cos2α=(1+cos 2α).
(2)公式的逆用:
①1±sin 2α=(sin α±cos α)2;
②sin α±cos α=sin.
1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)
(1)对∀α∈R,sin 2α=2sin α均不成立.( )
(2)sin2-cos2=cos =.( )
(3)sin α+cos α=.( )
(4)等式1+cos α=2sin2对∀α∈R均成立.( )
[答案] (1)× (2)× (3)× (4)×
2.下列各式中值为的是________.(填序号)
①2sin 15°cos 15°;②cos215°-sin215°;③2sin215°-1;④sin215°+cos215°.
② [2sin 15°cos 15°=sin 30°=,cos215°-sin215°=cos 30°=,2sin215°-1=-cos 30°=-,
sin215°+cos215°=1.]
3.若sin α=,α∈,则tan 2α=________.
- [∵α∈,sin α=,
∴cos α==,
∴tan α=2,
∴tan 2α===-.]
4.(2017·南京模拟)若tan α=,则=________.
[==tan α=.]
5.(教材改编)函数 f(x)=sin x+cos x的最小值为________.
-2 [函数f(x)=2sin的最小值是-2.]
应用倍角公式求值
(2017·无锡模拟)已知coscos=-,α∈.
(1)求sin 2α的值;
(2)求tan α-的值.
[解] (1)cos·cos
=cos·sin
=sin=-,
即sin=-.
∵α∈,
∴2α+∈,
∴cos=-,
∴sin 2α=sin
=sincos-cos·sin =.
(2)∵α∈,∴2α∈.
又由(1)知sin 2α=,∴cos 2α=-.
∴tan α-=-===-2×=2.
[规律方法] 给出某些角的三角函数式的值,求另外一些角的三角函数值,解题关键在于“变角”,使其角相同或具有某种关系.如本题中+=,从而先利用诱导公式变换函数名,进而逆用二倍角公式求值.
[变式训练1] (2017·南京、盐城二模)已知α为锐角,cos=.
(1)求tan的值;
(2)求sin的值. 【导学号:62172133】
[解] (1)因为α∈,所以α+∈,
所以sin==,
所以tan==2.
(2)因为sin=sin=2sincos=,
cos=cos=2cos2-1=-,
所以sin=sin=sincos-cossin =.
应用倍角公式化简
(1)化简:=________.
(2)化简:.
(1)2cos α [原式==2cos α.]
(2)原式=
===cos 2x.
[规律方法] 1.三角函数式的化简要遵循“三看”原则
(1)一看“角”,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式.
(2)二看“函数名称”,看函数名称之间的差异,从而确定使用的公式,最常见的是“切化弦”.
(3)三看“结构特征”,分析结构特征,找到变形的方向.
2.三角函数式化简的方法
弦切互化,异名化同名,异角化同角,降幂或升幂.
[变式训练2] 化简sin2+sin2-sin2α=________.
[法一:原式=+-sin2α
=1--sin2α=1-cos 2α·cos -sin2α=1--=.
法二:令α=0,则原式=+=.]
三角变换的简单应用
已知函数f(x)=sin2x-sin2,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在区间上的最大值和最小值. 【导学号:62172134】
[解] (1)由已知,有
f(x)=-
=-cos 2x
=sin 2x-cos 2x=sin.
所以f(x)的最小正周期T==π.
(2)因为f(x)在区间上是减函数,
在区间上是增函数,
且f=-,f=-,f=,
所以f(x)在区间上的最大值为,最小值为-.
[规律方法] 1.进行三角恒等变换要抓住:变角、变函数名称、变结构,尤其是角之间的关系;注意公式的逆用和变形使用.
2.把形如y=asin x+bcos x化为y=sin(x+φ),可进一步研究函数的周期、单调性、最值与对称性.
[变式训练3] 已知函数f(x)=sinsin x-cos2x.
(1)求f(x)的最小正周期和最大值;
(2)讨论f(x)在上的单调性.
[解] (1)f(x)=sinsin x-cos2x
=cos xsin x-(1+cos 2x)=sin 2x-cos 2x-=sin-.
因此f(x)的最小正周期为π,最大值为.
(2)当x∈时,0≤2x-≤π,
从而当0≤2x-≤,即≤x≤时,f(x)单调递增,
当≤2x-≤π,即≤x≤时,f(x)单调递减.
综上可知,f(x)在上单调递增;在上单调递减.
[思想与方法]
1.三角函数的求值与化简要注意观察角、函数名称、式子结构之间的联系,然后进行变换.
2.利用三角函数值求角要考虑角的范围.
3.与三角函数的图象与性质相结合的综合问题.借助三角恒等变换将已知条件中的函数解析式整理为f(x)=Asin(ωx+φ)的形式,然后借助三角函数图象解决.
[易错与防范]
1.利用辅助角公式asin x+bcos x转化时,一定要严格对照和差公式,防止弄错辅助角.
2.计算形如y=sin(ωx+φ),x∈[a,b]形式的函数最值时,不要将ωx+φ的范围和x的范围混淆.
课时分层训练(二十四)
A组 基础达标
(建议用时:30分钟)
一、填空题
1.已知sin 2α=,则cos2等于________.
[因为cos2=
====.]
2.设sin 2α=-sin α,α∈,则tan 2α的值是________.
【导学号:62172135】
[∵sin 2α=2sinαcos α=-sin α,
∴cos α=-,
又α∈,
∴sin α=,tan α=-,
∴tan 2α===.]
3.(2016·全国卷Ⅲ改编)若tan θ=-,则cos 2θ=________.
[∵cos 2θ==.
又∵tan θ=-,∴cos 2θ==.]
4.已知sin α=,α∈,则=________.
- [
=
=cos α-sin α.
∵sin α=,α∈,
∴cos α=-.
∴原式=-.]
5.(2017·苏州模拟)已知sin(α-45°)=-且0°<α<90°,则cos 2α的值为________. 【导学号:62172136】
[∵sin(α-45°)=-,
∴sin α-cos α=-,
∴2sin αcos α=,
∴sin α+cos α==,
∴sin α=,cos α=.
∴cos 2α=cos2α-sin2α=.]
6.(2016·山东高考改编)函数f(x)=(sin x+cos x)(cos x-sin x
)的最小正周期是________.
π [法一:∵f(x)=(sin x+cos x)(cos x-sin x)
=4
=4sincos =2sin,
∴T==π.
法二:∵f(x)=(sin x+cos x)(cos x-sin x)
=3sin xcos x+cos2x-sin2x-sin xcos x
=sin 2x+cos 2x
=2sin,
∴T==π.]
7.(2017·苏州模拟)若sin=,则cos=________.
【导学号:62172137】
- [cos=cos
=-cos=-
=-=-.]
8.化简+2=________.
-2sin 4 [+2
=+2
=+2
=-2cos 4+2(cos 4-sin 4)=-2sin 4.]
9.(2017·南通模拟)若α∈,且3cos 2α=sin,则sin 2α的值为________.
- [∵3cos 2α=sin,
∴3sin=sin,
∴3×2sincos=sin.
∴sin≠0,∴cos=,
即sin α+cos α=,
∴sin 2α=-=-.]
10.已知cos4α-sin4α=,且α∈,
则cos=______________.
[∵cos4α-sin4α=cos2α-sin2α=cos 2α=,
又α∈,∴2α∈(0,π).
∴sin 2α=.
∴cos=cos 2αcos-sin 2αsin
=cos 2α-sin 2α
=×-×
=.]
二、解答题
11.(2017·盐城期中)已知函数f(x)=sin xcos x-cos2x.
(1)求f(x)的最小正周期;
(2)若f(x)=-1,求cos的值.
[解] (1)因为f(x)=sin 2x-=sin 2x--=sin-,
所以f(x)的最小正周期为T==π.
(2)因为f(x)=-1,所以sin-=-1,即sin=-,
所以cos=cos=sin=-.
12.已知函数f(x)=cos2x+sin xcos x,x∈R.
(1)求f的值;
(2)若sin α=,且α∈,求f.
[解] (1)f=cos2+sincos
=2+×=.
(2)因为f(x)=cos2x+sin xcos x=+sin 2x
=+(sin 2x+cos 2x)=+sin.
所以f=+sin
=+sin=+.
又因为sin α=,且α∈,
所以cos α=-,
所以f=+
=.
B组 能力提升
(建议用时:15分钟)
1.函数f(x)=3sin cos +4cos2(x∈R)的最大值等于________.
[由题意知f(x)=sin x+4×=sin x+2cos x+2≤+2=.]
2.如图241,圆O与x轴的正半轴的交点为A,点C,B在圆O上,且点C位于第一象限,点B的坐标为,∠AOC=α.若|BC|=1,则cos2-sincos-的值为________.
图241
[由题意得|OB|=|OC|=|BC|=1,从而△OBC为等边三角形,∴sin∠AOB=sin=,
∴cos2-sin·cos-=·--=-sin α+cos α=sin=sin=sin=.]
3.已知α,β∈(0,π),且tan(α-β)=,tan β=-,求2α-β的值.
[解] ∵tan α=tan[(α-β)+β]
=
==>0,
∴0<α<.
又∵tan 2α===>0,
∴0<2α<,
∴tan(2α-β)=
==1.
∵tan β=-<0,
∴<β<π,-π<2α-β<0,∴2α-β=-.
4.已知函数f(x)=2sin xsin.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当x∈时,求函数f(x)的值域.
[解] (1)f(x)=2sin x=×+sin 2x=sin+.
所以函数f(x)的最小正周期为T=π.
由-+2kπ≤2x-≤+2kπ,k∈Z,
解得-+kπ≤x≤+kπ,k∈Z,
所以函数f(x)的单调递增区间是,k∈Z.
(2)当x∈时,2x-∈,
sin∈,
f(x)∈.
故f(x)的值域为.