- 386.50 KB
- 2021-04-15 发布
2018-2019学年河北省唐县第一中学高二上学期期中考试文科数学试题
一、选择题(60分)
1、从装有3个红球和3个白球的口袋里任取3个球,那么互斥而不对立的两个事件是( )
A.至少2个白球,都是红球 B.至少1个白球,至少1个红球
C.至少2个白球,至多1个白球 D.恰好1个白球,恰好2个红球
2、总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
7816 6572 0802 6314 0702 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
A.08 B.07 C.02 D.01
3、椭圆的一个焦点是,那么实数的值为( )
A. B. C. D.
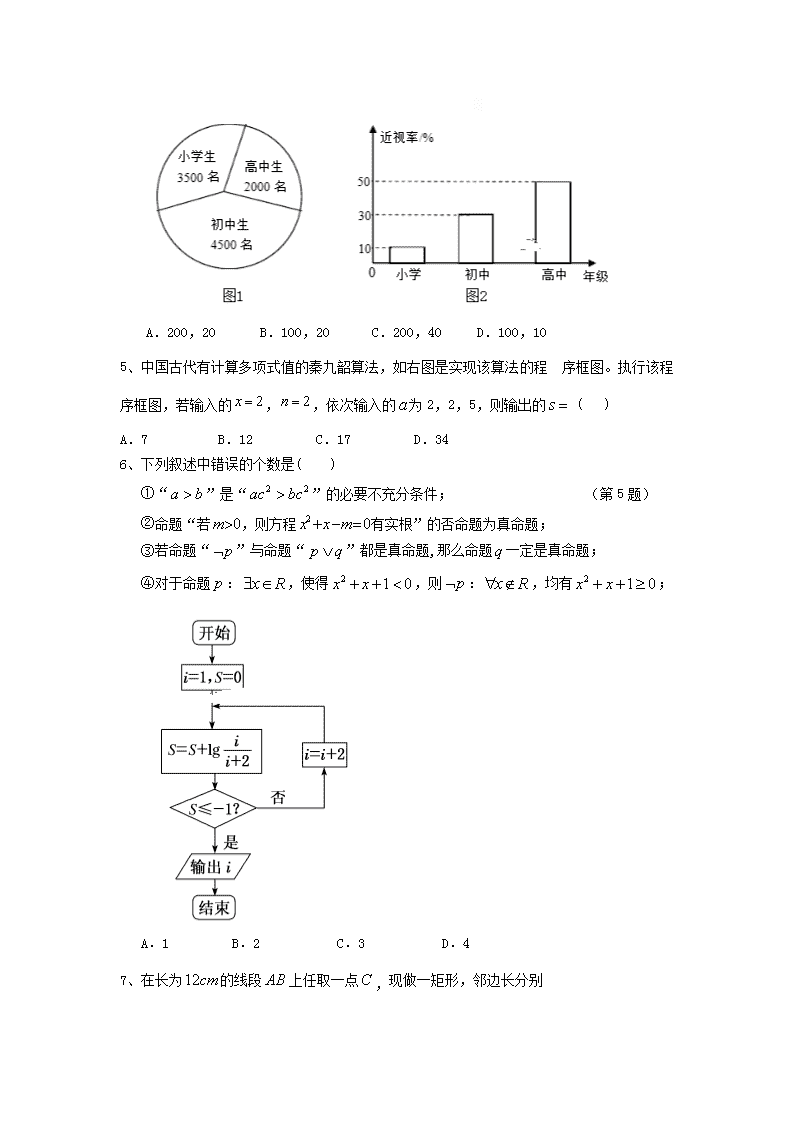
4、已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地中小学生的近
视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生
近视人数分别是( )
A.200,20 B.100,20 C.200,40 D.100,10
5、中国古代有计算多项式值的秦九韶算法,如右图是实现该算法的程 序框图。执行该程序框图,若输入的,,依次输入的为2,2,5,则输出的 ( )
A.7 B.12 C.17 D.34
6、下列叙述中错误的个数是( )
①“”是“”的必要不充分条件; (第5题)
②命题“若,则方程有实根”的否命题为真命题;
③若命题“”与命题“”都是真命题,那么命题一定是真命题;
④对于命题:,使得,则:,均有;
A.1 B.2 C.3 D.4
7、在长为的线段上任取一点,现做一矩形,邻边长分别
等于线段的长,则该矩形面积大于20cm2的概率为( )
A. B. C. D.
8、执行右图所示的程序框图,则输出的结果为( ).
A.8 B.9 C. 10 D. 11
9、已知P是直线l:3x-4y+11=0上的动点,PA,PB是圆x2+y2-2x-2y+1=0的两条切线(A,B是切点),C是圆心,那么四边形PACB的面积的最小值是( )
A. B.2 C. D.2
10、5件产品中,有3件一等品和2件二等品,从中任取2件,那么以为概率的事件是( )
A.都不是一等品 B.恰有一件一等品
C.至少有一件一等品 D.至多一件一等品
11、已知直线与圆交与两点,点在圆上,且,则满足条件的点的个数为( )
A.1 B.2 C.3 D.4
12、若双曲线:的一条渐近线被圆所截
得的弦长为2,则的离心率为( )
A.2 B. C. D.
二、填空题(20分)
13、已知双曲线的焦距为2,且双曲线的实轴长是虚轴长的2倍,则双曲线的方程为 .
14、已知命题,命题,若命题是真命题,则实数的取值范围是__________
15、已知圆过 (1,3)作圆的切线,则切线的方程 .
16、若一组数据的平方和是50,平均数是2,方差是1,则这组数据的个数为 .
三、解答题(70分)
17、
为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,某班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示(把频率当作概率).
(1)求甲、乙两人成绩的平均数和中位数;
(2)现要从甲、乙两人中选派一人参加比赛,从
统计学的角度,你认为派哪位学生参加比较合适?
18、甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
①若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
②若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
19、 某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),
[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求第四小组的频率;
(2)估计这次考试的平均分和中位数(精确到0.01);
(3)从成绩是40~50分及90~100分的学生中选两人,记他们的成绩分别为,求满足“”的概率.
20、 已知椭圆)的一个顶点A(2,0),离心率为,直线
与椭圆C交于不同的两点.
(1)求椭圆的方程;
(2)当△AMN的面积为时,求实数的值.
21、在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在市的区开设分店,为了确定在该区开设分店的个数,该公司对在该市其他区开设的分店的数据作了初步处理后得到下列表格.记表示在各区开设分店的个数,表示这个分店的年收入之和.
(个)
2
3
4
5
6
(百万元)
2.5
3
4
4.5
6
(1)该公司已经过初步判断,可用线性回归模型拟合与的关系,求关于 的线性回归方程;
(2)假设该公司在区获得的总年利润(单位:百万元)与之间的关系
,请结合(1)中的线性回归方程,估算该公司应在区开设多少个分店时,才能使区平均每个分店的年利润最大?
(参考公式
22、已知为椭圆的左右焦点,点为其上一点,
且有.
(1)求椭圆的标准方程;
(2)圆是以,为直径的圆,直线与圆相切,并与椭圆
交于不同的两点,若,求的值.
高二文科数学答案
一、选择题(60分)
1-5、 ADDAC 6-10、 BCBCD 11-12、 CA
二、填空题(20分)
13、-y2=1 14 、 15、x=1或3x+4y-15=0 16、10
三、解答题(70分)
17、解:(1)由茎叶图可知甲、乙两人成绩的平均数为
,
,
甲、乙两人成绩的中位数为
, .
(2)派甲参加比较合适,理由如下:
,
∵, ,
∴两人的平均成绩相等,但甲的成绩比较稳定,派甲参加比较合适.
18、 ①甲校两男教师分别用A,B表示,女教师用C表示;
乙校男教师用D表示,两女教师分别用E,F表示.
从甲校和乙校报名的教师中各任选1名的所有可能的结果为:(A,D)
(A,E),
(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F)共9种.
从中选出两名教师性别相同的结果有:(A,D),(B,D),(C,E),(C,F)共4种,选出的两名教师性别相同的概率为P=.
②从甲校和乙校报名的教师中任选2名的所有可能的结果为:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种,
从中选出两名教师来自同一学校的结果有:
(A,B),(A,C),(B,C),(D,E),(D,F),(E,F)共6种,选出的两名教师来自同一学校的概率为P==.
19、(1)由频率分布直方图可知
所以第4小组的频率为:1﹣0.1﹣0.15﹣0.15﹣0.25﹣0.05=0.3.
(2)由频率分布直方图可得平均分为:
0.1×45+0.15×55+0.15×65+0.3×75+0.25×85+0.05×95=71
第一、二、三组的频率之和为0.1+0.15+0.15=0.4
所以中位数= 70+≈73.33
(3) 由频率分步直方图可得,成绩是40~50分的有40×0.1=4人,记为1,2,3,490~100分的学生有40×0.05=2人,记为a,b.
记“|x﹣y| ≤10”为事件A,
基本事件有(1,2) (1,3) (1,4) (1,a) (1,b) (2,3) (2,4) (2,a) (2,b) (3,4) (3,a) (3,b) (4,a) (4,b) (a,b) 共计15个., 事件A中包含的基本事件数为 P(A)=.
20、 (1)∵a=2,e==,∴c=,b=.椭圆C:+=1.
(2)设M(x1,y1),N(x2,y2),则由消y,得(1+2k2)x2-4k2x+2k2-4=0.
∵直线y=k(x-1)恒过椭圆内一点(1,0),
∴Δ>0恒成立.
由根与系数的关系,得x1+x2=,x1x2=.
S△AMN=×1×|y1-y2|=×|kx1-kx2|
===.
即7k4-2k2-5=0,解得k=±1.
21、解、(1)代入数据得:,,,∴.
(2)由题意,可知总收入的预报值与之间的关系为:,设该区每个分店的平均利润为,则,故的预报值与之间的关系为,
则当时,取到最大值,
22、(1)∵2a=4,∴a=2.
∴设椭圆方程为+=1.∵椭圆C过点(1,),∴+=1.
∴b2=3,∴椭圆方程为+=1.
(2)∵直线l与⊙O相切设C到l的距离为d,则d=r.
即=1,∴m2=1+k2.①
由得(3+4k2)x2+8kmx+4m2-12=0.
设A,B坐标为A(x1,y1),B(x2,y2),
∴x1+x2=,x 1·x2=.
∴y1·y2=k2x1x2+km(x1+x2)+m2=.
∴x1x2+y1y2=.②①代入②,得x1x2+y1y2=.∵·=x1x2+y1y2=-,∴=-,∴k=±.