- 159.50 KB
- 2021-04-15 发布
北京市十一学校2019-2020学年高二上学期期中考试数学试题
一、选择题(本大题共8小题)
1. 下列叙述中,错误的一项为( )
A. 棱柱的面中,至少有两个面相互平行
B. 棱柱的各个侧面都是平行四边形
C. 棱柱的两底面是全等的多边形
D. 棱柱中两个互相平行的平面一定是棱柱的底面
2. 下列函数中,在定义域内为奇函数,且在(0,+∞)上为减函数的是( )
A. B. C. D.
3. 圆锥的高缩小为原来的,底面半径扩大为原来的2倍,则它的体积是原来体积的( )
A. B. C. D.
4. 设α,β是两个不同的平面,m是直线且m⊂α,“m∥β“是“α∥β”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
5. 双曲线(a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为30°的直线交双曲线右支于M点,若MF2垂直于x轴,则双曲线的离心率为( )
A.
B.
C.
D.
6. △ABC的内角A,B,C的对边分别为a,b,c,若A=60°,b=10,则结合a的值解三角形有两解的为( )
A. B. C. D.
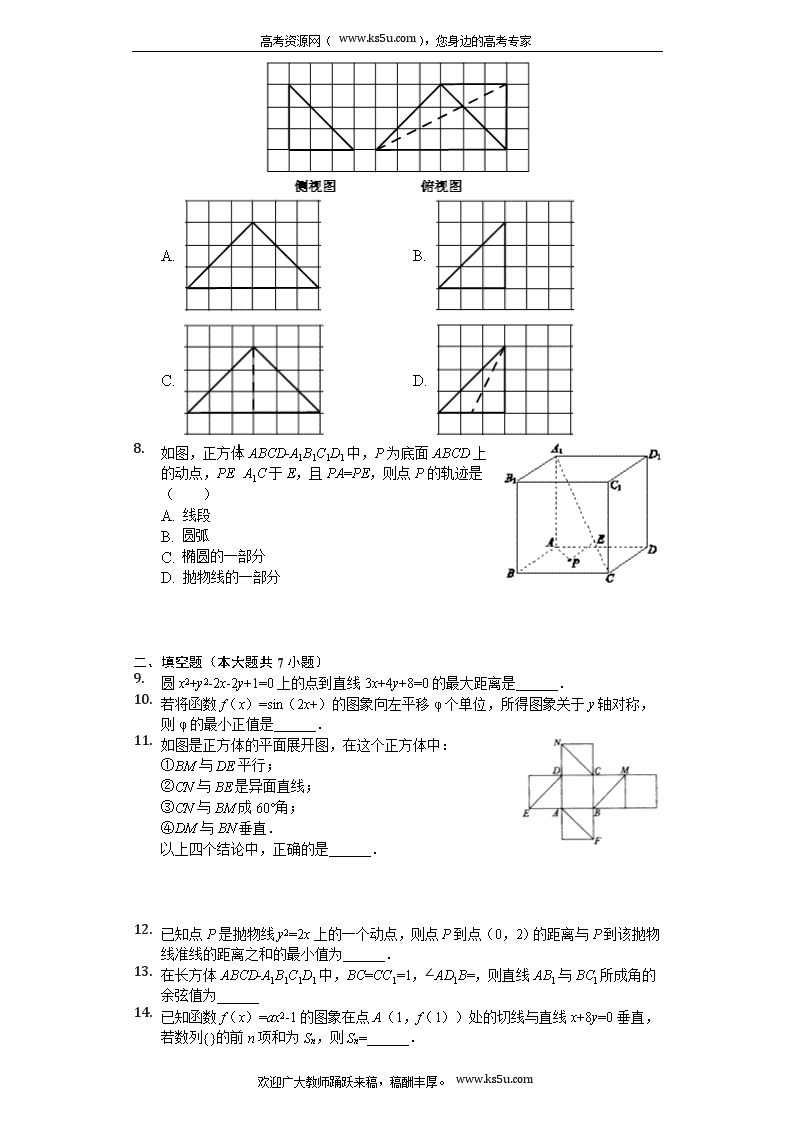
7. 如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( )
A. B.
C. D.
1. 如图,正方体ABCD-A1B1C1D1中,P为底面ABCD上的动点,PE⊥A1C于E,且PA=PE,则点P的轨迹是( )
A. 线段
B. 圆弧
C. 椭圆的一部分
D. 抛物线的一部分
二、填空题(本大题共7小题)
2. 圆x2+y2-2x-2y+1=0上的点到直线3x+4y+8=0的最大距离是______.
3. 若将函数f(x)=sin(2x+)的图象向左平移φ个单位,所得图象关于y轴对称,则φ的最小正值是______.
4. 如图是正方体的平面展开图,在这个正方体中:
①BM与DE平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个结论中,正确的是______.
5. 已知点P是抛物线y2=2x上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为______.
6. 在长方体ABCD-A1B1C1D1中,BC=CC1=1,∠AD1B=,则直线AB1与BC1所成角的余弦值为______
7. 已知函数f(x)=ax2-1的图象在点A(1,f(1))处的切线与直线x+8y=0垂直,若数列{}的前n项和为Sn,则Sn=______.
1. 如图,四面体 ABCD的一条棱长为 x,其余棱长均为 1,记四面体 ABCD的体积为F(x),则函数F(x)的单调增区间是______;最大值为______.
三、解答题(本大题共5小题)
2. 已知函数f(x)=sin2ωx+sinωx•sin(ωx+)-1(ω>0)的相邻两条对称轴之间的距离为.
(1)求ω的值;
(2)当x∈[-,]时,求函数f(x)的值域.
3. 已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,满足a1=b1=2,2a2=b2,S2+T2=13.
(1)求数列{an},{bn}通项公式;
(2)设cn=an+bn,求数列{cn}的前n项和Hn.
4. 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=AD,点F是棱PD的中点,点E为CD的中点.
(1)证明:EF∥平面PAC;
(2)证明:AF⊥PC.
5. 已知椭圆C:的右焦点,点在椭圆C上.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)直线l过点F,且与椭圆C交于A,B两点,过原点O作直线l的垂线,垂足为P,如果△OAB的面积为(λ为实数),求λ的值.
1.
已知函数f(x)=a(x-2lnx)-x2+2x.
(1)讨论f(x)的单调性;
(2)若f(x)有两个不同的零点,求a的取值范围.
答案和解析
1.【答案】D
【解析】解:定义1:上下底面平行且全等,侧棱平行且相等的封闭几何体叫棱柱.
定义2:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围城的几何体叫棱柱;
正4棱柱,正6棱柱中,相对的侧面都是互相平行的平面,故D错;
故选:D.
根据棱柱的定义可知ABC对,正4棱柱,正6棱柱中,相对的侧面都是互相平行的平面,故D错;
考查棱柱的定义,以及对空间几何体棱柱的理解;
2.【答案】D
【解析】解:A.f(x)的定义域为(0,+∞),函数为非奇非偶函数;
B.f(-x)=2-(-x)2=2-x2=f(x),则f(x)是偶函数,不满足条件;
C.f(x)为指数函数,单调递减,为非奇非偶函数;
D.f(-x)=-==-f(x),则f(x)是奇函数,当x>0时,函数f(x)为减函数,满足条件.
故选:D.
根据函数奇偶性和单调性的定义分别进行判断即可.
本题主要考查函数奇偶性和单调性的判断,结合常见函数的单调性和奇偶性的性质是解决本题的关键.
3.【答案】C
【解析】解:设一个圆锥的底面半径为r,高为h,则其体积V=;
圆锥的高缩小为原来的,底面半径扩大为原来的2倍,则所得圆锥的底面半径为2r,高为,
体积为.
∴.
∴它的体积是原来体积的.
故选:C.
设一个圆锥的底面半径为r,高为h,利用圆锥体积公式求其体积,再求出变换后的圆锥的体积,则答案可求.
本题考查圆锥体积的求法,是基础的计算题.
4.【答案】B
【解析】解:m⊂α,m∥β得不到α∥β,因为α,β可能相交,只要m和α,β的交线平行即可得到m∥β;
α∥β,m⊂α,∴m和β没有公共点,∴m∥β,即α∥β能得到m∥β;
∴“m∥β”是“α∥β”的必要不充分条件.
故选:B.
m∥β并得不到α∥β,根据面面平行的判定定理,只有α内的两相交直线都平行于β,而α∥β,并且m⊂α,显然能得到m∥β,这样即可找出正确选项.
考查线面平行的定义,线面平行的判定定理,面面平行的定义,面面平行的判定定理,以及充分条件、必要条件,及必要不充分条件的概念.
5.【答案】B
【解析】解:如图在Rt△MF1F2中,∠MF1F2=30°,F1F2=2c
∴,
∴
∴,
故选:B.
先在Rt△MF1F2中,利用∠MF1F2和F1F2求得MF1和MF2,进而根据双曲线的定义求得a,最后根据a和c求得离心率.
本题主要考查了双曲线的简单性质,属基础题.
6.【答案】B
【解析】解:由正弦定理,有,
∴=,
∵三角形有两解,∴sinB<1且b>a,
∴,
因此由选项知,只有a=9时符合条件,
故选:B.
根据正弦定理可得,然后根据三角形有两解可得sinB<1且b>a,从而得到a的范围.
本题考查了正弦定理和三角形中大边对大角等知识的应用,考查了转化思想,属中档题.
7.【答案】A
【解析】解:由已知中锥体的侧视图和俯视图,
可得该几何体是三棱锥,
由侧视图和俯视图可得,该几何的直观图如图P-ABC所示:
顶点P在以BA和BC为邻边的平行四边形ABCD上的射影为CD的中点O,
故该锥体的正视图是:
故选A
由已知中锥体的侧视图和俯视图,画出该几何的直观图,进而可得该锥体的正视图.
本题考查的知识点是简单空间几何体的三视图,其中根据已知中的三视图,画出直观图是解答的关键.
8.【答案】A
【解析】解:连接A1P,由题意知A1A⊥AP,
因为PE⊥A1C,且PA=PE,
所以△A1AP≌△A1EP,
所以A1A=A1E,即E
为定点.
因为PA=PE,
所以点P位于线段AE的中垂面上,
又点P在底面上,
所以点P的轨迹为两平面的交线,即点P的轨迹是线段.
故选A.
由PE⊥A1C于E,且PA=PE,得到点E是定点,然后根据PA=PE,得到点P位于A,E的中垂面上,从而得到点P的轨迹.
本题主要考查空间直线的位置关系的判断,以及空间点的轨迹的求法,综合性较强,难度较大.
9.【答案】4
【解析】解:由题意可得,圆的标准方程为(x-1)2+(y-1)2=1,
圆心的坐标为(1,1),半径r=1,
∴圆心到直线的距离
,
所以所求最大距离是4,
故答案为:4.
根据图象可知,最大距离是圆心到直线的距离与半径长之和.
本题主要考查直线与圆的位置关系,属于基础题.
10.【答案】
【解析】解:将函数f(x)=sin(2x+)的图象向左平移φ个单位,可得y=sin(2x++2φ)的图象,
再根据所得图象关于y轴对称,可得+2φ=+kπ,k∈Z,
则φ的最小正值为,
故答案为:.
利用函数y=Asin(ωx+φ)的图象变换规律,三角函数的图象的对称性,求出φ的最小正值.
本题主要考查函数y=Asin(ωx+φ)的图象变换规律,三角函数的图象的对称性,属于基础题.
11.【答案】③④
【解析】【分析】
本题考查正方体的结构特征,异面直线的判定,异面直线及其所成的角,空间中直线与直线之间的位置关系,几何体的折叠与展开,考查空间想象能力,是基础题.
将展开图复原为几何体,如图,容易判断选项的正误,得出结果.
【解答】
解:展开图复原的正方体如图,不难看出:
①BM与ED平行;错误的,是异面直线;
②CN与BE是异面直线,错误;是平行线;
③从图中连接AN,AC,由于几何体是正方体,故三角形ANC是等边三角形,所以AN与CN的夹角是60°,又AN∥BM,故CN与BM成60°;正确;
④DM⊥NC,DM⊥BC,所以DM⊥平面BCN,所以DM与BN垂直.正确
判断正确的答案为③④.
故答案为:③④.
12.【答案】
【解析】解:依题设P在抛物线准线的投影为P',抛物线的焦点为F,则,
依抛物线的定义知P到该抛物线准线的距离为|PP'|=|PF|,
则点P到点A(0,2)的距离与P到该抛物线准线的距离之和
.
故答案为:.
先求出抛物线的焦点坐标,再由抛物线的定义可得d=|PF|+|PA|≥|AF|,再求出|AF|的值即可.
本小题主要考查抛物线的定义解题,考查了抛物线的应用,考查了学生转化和化归,数形结合等数学思想.
13.【答案】
【解析】解:如图所示,建立空间直角坐标系.
∵长方体中,BC=CC1=1,∠AD1B=,
∴AD1=,AB=AD1tan=.
∴A(1,0,0),B1(1,,1),B(1,,0),C1(0,,1).
∴=(0,,1),=(-1,0,1),
∴cos===.
故答案为:.
如图所示,建立空间直角坐标系.根据长方体中,BC=CC1=1,∠AD1B=,可得AD1=,AB=AD1tan=.利用向量夹角公式即可得出.
本题考查了长方体的性质、向量夹角公式、空间线面位置关系,考查了推理能力与计算能力,属于中档题.
14.【答案】
【解析】解:函数f(x)=ax2-1的导数为f′(x)=2ax,
可得f(x)在x=1处的切线斜率为2a,
切线与直线x+8y=0垂直,可得2a=8,即a=4,
则f(x)=4x2-1,
==(-),
可得Sn=(1-+-+…+-)
=(1-)=.
故答案为:.
求得f(x)的导数,可得切线的斜率,由两直线垂直的条件,可得a=4,再由裂项相消求和,可得所求和.
本题考查导数的运用:求切线的斜率,数列的裂项相消求和,两直线垂直的条件,考查运算能力,属于基础题.
15.【答案】,;
【解析】解:如图所示,设BC=x,AB=AC=AD=CD=BD=1.
取AD的中点O,
连接OB,OC,则OB⊥AD,OC⊥AD,OB=OC=.
又OB∩OC=O,则AD⊥平面OBC
,
取BC的中点E,连接OE,则OE⊥BC,
OE==.
∴S△OBC==.
∴F(x)=
=×1
=(0<x<).
F′(x)=,
令F′(x)≥0,解得,此时函数F(x)单调递增;令F′(x)<0,解得,此时函数F(x)单调递减法.
因此当x=时,F(x)取得最大值,==.
故答案分别为:,.
如图所示,设BC=x,AB=AC=AD=CD=BD=1.取AD的中点O,连接OB,OC,则OB⊥AD,OC⊥AD,OB=OC=.又OB∩OC=O,则AD⊥平面OBC.取BC的中点E,连接OE,则OE⊥BC,可得OE,可得F(x)==(0<x<).利用导数研究其单调性即可得出.
本题考查了利用导数研究函数的单调性极值与最值、三棱锥的体积计算公式、线面垂直的判定定理、勾股定理、等边三角形的性质,考查了推理能力与计算能力,属于中档题.
16.【答案】解:(1)=,
∵函数f(x)的最小正周期为π,且ω>0,
∴=π,
∴解得ω=1,
(2)∵x∈[-,],
∴2x-∈[-,],根据正弦函数的图象可得:
当2x-=,即x=时,g(x)=sin(2x-)取最大值1.
当2x-=-,即x=-时,g(x)=sin(2x-)取最小值-,
∴,即f(x)的值域为.
【解析】(1)利用三角函数恒等变换的应用可得f(x)=,利用正弦函数的周期公式即可求解ω的值.
(2)由已知可得2x-∈[-,],根据正弦函数的图象即可解得函数f(x)的值域.
本题主要考查了三角函数恒等变换的应用,正弦函数的周期公式,正弦函数的图象和性质,考查了转化思想和数形结合思想的应用,属于中档题.
17.【答案】解:(1)设公差为d等差数列{an}的前n项和为Sn,公比为q的等比数列{bn}的前n项和为Tn,满足a1=b1=2,2a2=b2,S2+T2=13.
所以:,解得,所以an=2+(n-1)=n+1,.
(2)由于cn=an+bn=n+1+2•3n-1,
所以Hn=(1+2+…+n)+n+2(30+31+…+3n-1)==.
【解析】(1)首先利用已知条件求出数列的通项公式.
(2)利用分组法求出数列的和.
本题考查的知识要点:数列的通项公式的求法及应用,分组法求数列的和,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
18.【答案】证明:(1)点F是棱PD的中点,点E为CD的中点.
∴EF∥PC,
∵EF⊄平面PAC,PC⊂平面PAC,
∴EF∥平面PAC.
(2)∵在四棱锥P-ABCD中,底面ABCD是正方形,
PA⊥底面ABCD,且PA=AD,点F是棱PD的中点,
∴AF⊥PD,PA⊥CD,AD⊥CD,
∵PA∩AD=A,∴CD⊥平面PAD,
∵AF⊂平面PAD,∴CD⊥AF,
∵PD∩CD=D,∴AF⊥平面PCD,
∵PC⊂平面PCD,∴AF⊥PC.
【解析】(1)推导出EF∥PC,从而EF∥平面PAC.
(2)推导出AF⊥PD,PA⊥CD,AD⊥CD,从而CD⊥平面PAD,进而CD⊥AF,AF⊥平面PCD,由此能证明AF⊥PC.
本题考查线面平行、线线垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查数形结合思想,考查运算求解能力,是中档题.
19.【答案】解:(Ⅰ)由题意知:c=,左焦点F′(-,0).
根据椭圆的定义得:2a=|MF′|+|MF|=+,
解得a=2,∴b2=a2-c2=4-3=1,
∴椭圆C的标准方程为:+y2=1;
(Ⅱ)由题意知,S△ABC=|AB|•|OP|=,
整理得:λ=|OP|2-.
①当直线l的斜率不存在时,l的方程为:x=,
此时|AB|=1,|OP|=,
∴λ=|OP|2-=-1;
②当直线l的斜率存在时,设直线l的方程为:y=k(x-),
设A(x1,y1),B(x2,y2),
联立,消去y整理得:(1+4k2)x2-8k2x+12k2-4=0,
显然△>0,则x1+x2=-,x1x2=,
∵y1=k(x1-),y2=k(x2-),
∴|AB|=
=•
=4•,
∴|OP|2=()2=,
此时,λ=-=-1;
综上所述,λ为定值-1.
【解析】(Ⅰ)通过右焦点可知:c=,左焦点F′(-,0),利用2a=|MF′|+|MF|可得a=2,进而可得结论;
(Ⅱ)通过S△ABC=,可得λ=|OP|2-,对直线l的斜率存在与否进行讨论.当直线l的斜率不存在时,易得λ=-1;当直线l的斜率存在时,设直线l的方程并与椭圆C方程联立,利用韦达定理、两点间距离公式、点到直线的距离公式计算亦得λ=-1.
本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.
20.【答案】解:(1)函数f(x)=a(x-2lnx)-x2+2x.定义域为(0,+∞),
f′(x)=a(1-)-x+2=(x-2)(a-x),(x>0)
①a≤0时,a-x<0,
当x∈(0,2).f′(x)>0,f(x)单调递增;
当x∈(2,+∞).f′(x)<0,f(x)单调递减;
②0<a<2时,f′(x)=0,解得x=2或x=a,
当x∈(0,a),f′(x)<0,f(x)单调递减;
当x∈(a,2),f(x)>0,f(x
)单调递增,
当x∈(2,+∞),f′(x)<0,f(x)单调递减;
③a=2时,f′(x)=-(x-2)2≤0,f(x)在(0,+∞)单调递减;
④a>2时,f′(x)=0,解得x=2或x=a,
当x∈(0,2),f′(x)<0,f(x)单调递减;
x∈(2,a),f′(x)>0,f(x)单调递增;
x∈(a,+∞),f′(x)<0,f(x)单调递减;
(2)由(1)得当a=0时,f(x)=-x2+2x在定义域上只有一个零点,
当a<0时,由(1)可得,
要使f(x)有两个零点,则f(2)>0,即f(2)=a(2-2ln2)+2>0,
所以<a<0,
下证f(x)有两个零点,
取x=,f()=a(-2×)-()2+2
=a-(-2)2<0,
满足f()•f(2)<0,故f(x)在(0,2)有且只有一个零点;
因为f(4)=a(4-2ln4)<0,
满足f(2)•f(4)<0,故f(x)在(2,+∞)有且只有一个零点;
当0<a<2时,由(1)可得当x∈(0,2),
f(x)≥f(a)
=a(a-2lna)-a2+2a
=a2+2a(1-lna)>0,
故f(x)在(0,2)无零点,又因为f(x)在(2,+∞)单调递减,
∴f(x)在(0,+∞)至多一个零点,不满足条件;
当a=2时,f(x)在(0,+∞)单调递减,
∴f(x)在(0,+∞)至多一个零点,不满足条件;
当a>2时,由(1)可得当x∈(0,a),
f(x)≥f(2)=a(2-2ln2)+2>0,
故f(x)在(0,a)上无零点,
又因为f(x)在(a,+∞)单调递减,
∴f(x)在(0,+∞)至多一个零点,不满足条件;
∴满足条件a的取值范围<a<0.
【解析】本题考查函数的导数应用,函数的单调性以及分类讨论思想的应用,考查计算能力,属于较难题.
(1)求函数的导数,分类讨论a的范围,可得f(x)的单调性;
(2)由(1)可得,要使f(x)有两个零点,则f(2)>0,即f(2)=a(2-2ln2)+2>0,所以<a<0,证明f(x)有两个零点,利用函数的单调性和讨论a的范围可求a的取值范围.